¿P ≠ NP?

El problema P versus NP es uno de los siete Problemas del Milenio de la Fundación Clay. Vinay Deolalikar, investigador de los Laboratorios de Hewlett-Packard en Palo Alto (California, USA) acaba de anunciar en un artículo que ha resuelto el problema en el sentido que N no es igual a NP. Si eso fuera así, se habría hecho acreedor al premio de un millón de dólares. Sin embargo, la cuestión no está tan clara.

P versus NP

Este es un problema de enorme importancia para la computación científica. Está relacionado con la rapidez que un ordenador puede realizar una tarea, imaginemos por ejemplo, factorizar un número. Esta es una tarea fácil si se trata de las que recordamos de nuestros años escolares (recordemos lo de descomponer un número en sus factores primos), pero muy compleja cuando hablamos de números muy grandes. El tema de la factorización es crucial en criptografía; el código RSA está basado en conocer números primos muy grandes, multiplicarlos y obtener un número inmenso cuya descomposición va a ser una tarea titánica y así garantizamos el secreto de nuestras comunicaciones.

Una manera precisa de establecer el problema P versus NP en términos matemáticos sería esta: Determinar si cada lenguaje aceptado por algún algoritmo no determinístico en tiempo polinómico es también aceptado por algún algoritmo determinístico en tiempo polinómico. Hay que recurrir a la definición de modelo formal de un ordenador, como la máquina de Turing, etc. Pero tratamos aquí de dar una idea sencilla y no técnica del problema.

Recordemos que un algoritmo es un procedimiento para resolver algún problema, y que el agoritmo lo podemos colocar en un ordenador. Una cuestión esencial es la eficiencia del algoritmo, o en otras palabras, cuánto tiempo de computación necesita para resolverlo; más concretamente, ¿cómo depende el número de cálculos necesarios de los datos iniciales? Será un problema P si esta dependencia es polnómica y no P (no confundir con NP) si no lo es. En palabras llanas, un problema P es fácil de resolver; un problema no P, no.  Por ejemplo, colocar una lista de números en orden creciente es un problema P; el problema del viajante (el camino más corto a seguir por un viajante para visitar todas las ciudades de una ruta comercial), se cree que es no P.

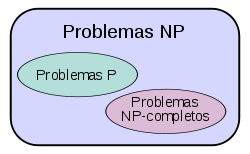
Un problema se puede ver que es P si se encuentra un algoritmo adecuado, pero para un problema no P, se trata de probar todos los algoritmos posibles y ver que ninguno resuelve el problema en tiempo polinómico.

NP no es lo mismo que no P. NP significa que puede ver fácilmente si una solución es correcta a o no, pero encontrar todas las soluciones sería muy largo. Por ejemplo, si nos dan una solución de un rompecabezas, enseguida veremos si es correcta o no, pero resolverlo puede ser muy díficil.

Para que nos entendamos con lo que es un  problema P y un problema NP, veamos este ejemplo que se puede encontrar en la descripción del mismo en la web de la Fundación Clay.

Imaginemos una residencia de estudiantes que puede alojar a 100 de ellos, y a la que han concurrido 400 estudiantes. Los 100 estudiantes deben ser alojados en habitaciones dobles, y el director tiene una lista de parejas de estudiantes que no podrían compartir habitación. El número posible de listas de 100 parejas que se podrían formar con los 400 estudiantes es enorme, así que sería una tarea imposible calcularlas todas. Pero si damos una lista, es muy fácil ver si es aceptable o no, porque bastaría ver si contiene o no una de las parejas prohibidas.

Por tanto, si P fuera igual a NP, esto significaría que sería fácil de comprobar si las posibles soluciones son correctas, pero también fácil el encontrar las soluciones.

Por cierto, el buscaminas es un ejemplo de lo que se llama un problema NP completo.

¿La solución?

El 6 de agosto, Vinay Deolalikar, matemático indio que está trabajando en los Laboratorios de Hewlett-Packard en Palo Alto (California, USA) envió su manuscrito (de 66 páginas en tamaño de 10pt, 102 páginas en tamaño de 12pt) a varios matemáticos relevantes para su lectura. Ahora prepara la versión final para enviar a una revista.

Como se pueden imaginar, el revuelo en la comunidad matemática está siendo enorme, y matemáticos de la talla de Timothy Gowers, Gil Kalai, Ken Regan, Terence Tao, Suresh Venkatasubramanian y otros, están revisándolo todo, y, esto es una característica muy particular en la comunidad matemática internacional, dispuestos a echar una mano a Vinay en cualquier desarrollo o dificultad en que él lo necesite. Así lo ha declarado públicamente Terry Tao.

Recomendamos seguir atentos al tema, los próximos meses serán apasionantes y dictarán si la demostración de Vinay Deolalikar sobrevivirá o no.

________________________

Manuel de León (CSIC y Real Academia de Ciencias) es Director del Instituto de Ciencias Matemáticas (ICMAT).