![]()
Primera lección de danza clásica para matemáticos
Seguro que no soy la única bailarina física-matemática, porque es indudable que el ballet es una tendencia en boga. Las últimas son el fitness, pilates y el ballet. Algo me dice que es la influencia de los ángeles de Victoria Secret, promociónandolas como las disciplinas que esculpen el cuerpo. Subirse a las puntas y tener el cuerpo de Adriana Lima, ¡allá vamos!
Sin embargo, he dado con pocos matemáticos que no me entorpezcan el paso (¡de baile!), por eso he decidido que quizás sea preferible enseñaros una primera lección traduciendo los nombres puristas en francés, por una somera descripción matemática.
¿Mejoraría nuestra percepción de la danza si os dijera que en realidad sólo debemos restringir nuestro movimiento a las de isometrías del grupo de Poincaré?
(Breve recordatorio: producto semidirecto de traslaciones en el espacio de Minkowski con el grupo de Lorentz, isomorfo al ortogonal generalizado SO(3,1)).
Cuando nos enfrentamos a la pista de baile, nos encontramos inmersos en una variedad cuadridimensional que suponemos sin curvatura: en otras palabras, un espacio-tiempo de Minkowski.
En efecto, el destello de un buen movimiento, ¡es la combinación de translaciones, rotaciones en el espacio y en el tiempo! Desafortunadamente, en nuestra coreografía no podemos deshacer el traspié, porque no tenemos la inversión temporal de Poincaré.
La primera lección consiste en el posicionamiento de las piernas. Para ello, partimos de un sistema de referencia inercial posicionado en un plano cartesiano.
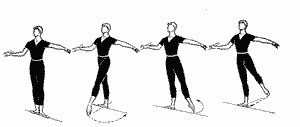
Nuestro origen será el (0,0). Nos posicionamos en la denominada posición inicial o sexta posición, descrita por la siguiente imagen:
Primera posición: partiendo de la posición inicial, realizar una rotación de noventa grados del pie derecho hacia la derecha e izquierdo a su izquierda. Los talones serán dos puntos fijos encontrados y nuestro eje vertical permanecerá invariante.
La figura resultante en el suelo, barrida por la planta del pie, es un semicírculo.
Segunda posición (à la seconde): partiendo de la primera posición, realizamos una translación a lo largo del eje X. Translación positiva en caso de que trabajemos con la pierna derecha. Mientras que el pie izquierdo permanece invariante, nuestro centro de masas se ha desplazado al punto medio del segmento comprendido entre nuestros pies, sobre el eje X. El desplazamiento, gradual. La derivada del vector posición de nuestro centro de masas respecto al tiempo es nula. Somos tan ligeros que no sentimos ni fuerzas externas ni internas sobre nuestro movimiento! (sí, una visión positiva de nuestro cuerpo nos dice que somos sólidos indeformables y continuos).
Cuarta posición: Pasamos desde la segunda a la cuarta posición realizando un ronde de jambe,
para que me entendáis, otra rotación de 90 grados en sentido horario o antihorario (en dehors, en dedans, ¡ojo, depende de la pierna utilizada!) hasta que el pie quede posicionado en el mismo eje de las Y, cortándolo horizontalmente.
Esto supone una traslación a lo largo de tal eje respecto de la posición inicial.
Quinta posición: Para terminar, cerraremos el cuarto de círculo dibujado deshaciendo la traslación del eje Y. ¡La posición resultante no ha sido, sin embargo, una operación de simetría propiamente dicha! La posición resultante final dista de la inicial en que el cierre se realiza punta-talón, en vez de como comenzamos, con talones encontrados.
En realidad, para obtener una operación de casi-simetría deberíamos hacer un cierre en tercera (no muy popular, aparentemente la ruptura de simetría de la quinta demuestra una mayor destreza en la rotación an dehors del cuadriceps).
La concatenación de posiciones cierran un semicírculo. Sobre este semicírculo confluye la construcción de todos los ejercicios. Repetir el movimiento comenzando con traslación negativa. Compleméntese el movimiento en ronde de jambe de 180 grados en vez de 90, realicése en l’air,
introduciendo una variable espacial más en nuestro espacio de configuración o redúzcanse al suelo par terre, en una dimensión menor.
Sobre esta pequeña base de operaciones de rotación y traslación, se contruye el movimiento.
No cabe duda de la simetría (al menos visual) o quasi-simetría matemática sobre la que se construye la base de cualquier baile.
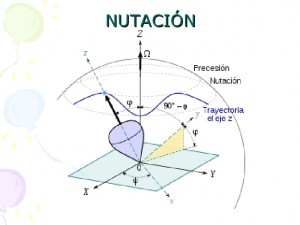
Aunque a veces, nosotros, los no profesionales de la danza convirtamos el modelo de una pirueta trompo simétrico con un punto fijo, en un modelo terráqueo con eje nuestro cuerpo que no sólo rota, sino que precesa y cabecea (movimiento de nutación)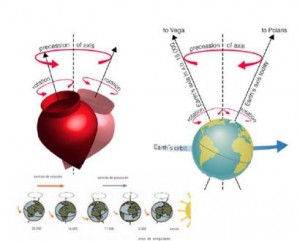
¡Si tan sólo nuestra precesión se notara cada 25.800 años!
Sobre la autora
Christina Sardón Muñoz estudió Ciencias Físicas en la Universidad de Salamanca, en la que defendió su tesis doctoral en 2015 sobre Sistemas de Lie. Su trabajo de investigación se centra en las aplicaciones de los sistemas de Lie al estudio de las ecuaciones diferenciales ordinarias y las ecuaciones diferenciales en derivadas parciales. Las matemáticas y la física teórica comparten su interés con la música y la danza.














Genial. Me ha encantado.
¡qué buen trabajo! aunque no soy ni matemático ni bailarín, sí un curioso observador de las redes y, bueno, que me interesa tener comunicación con Cristina, a propósito de un proyecto en pro de los estudiantes latinoamericanos de ciencias.
Hasta pronto
Muy interesante. Es que te estaba viendo en Boom y he sentido curiosidad por leerlo. Enhorabuena!!
A mí también me ha entrado la curiosidad viéndote en Boom de cómo ve el ballet una físico matemática bailarina.
[…] http://www.madrimasd.org/blogs/matematicas/2016/01/08/140489 […]
Gostei demais de ler esse blog, continuem assim!
Snaptik là một công cụ Snap TikTok hay còn gọi là Tik Snap chuyên hỗ trợ tải video tiktok VN DownloadTiktokVideos không logo hoặc có logo mới nhất hiện nay, miễn phí và hoàn toàn dễ dàng sử dụng chỉ có tại snaptik.vn với hơn hàng triệu lượt truy cập tải xuống video tiktok mỗi ngày.
I like this blogspot and i hope u always make good article from : Ricky