Más alla del formalismo: aplicaciones de teoría de grupos

La mayoría de lectores estará familiarizado con la teoría de grupos y son conscientes de su influencia en el álgebra moderna. Muchos, además, serán expertos en el manejo de esta estructura algebraica.

Desde el punto de vista matemático, la teoría de grupos se reduce a conceptos abstractos y super elaborados: grupos topológicos, grupos de transformaciones, teoría geométrica y combinatoria de grupos o teoría de sus representaciones. Son muchos los resultados obtenidos fruto de la investigación en este terreno: un hito de los años 70 fue la clasificación de los grupos simples, finito dimensionales. Desde el punto de vista formal, la teoría tiene una gran belleza y para un matemático basta el deleite de un enunciado conciso: “Cualquier grupo simple, finito es isomorfo a un grupo cíclico de orden primo, a un grupo alternante de orden cinco o superior, a un grupo de Lie simple (incluyéndose los grupos clásicos conocidos: unitario, simplético, ortogonal…) o a un grupo esporádico (uno de los 26 grupos excepcionales o twisted)”.-Teorema de Jordan-Hölder.

Sin embargo, aparte de la aparente simplicidad y precisión del enunciado (su demostración ocupa miles de páginas con contribuciones de más de cien autores), existen grandes aplicaciones de la teoría de grupos en otras disciplinas científicas. En particular, durante la segunda mitad del siglo XX, la teoría de grupos se ve afectada por las simetrías continuas (influenciadas por los grupos de Weyl, grupos finitos generados por reflexiones actuando en el espacio euclidiano), originando los grupos de Lie y sus técnicas asociadas: simetrías de Lie y grupos de transformaciones, que han servido de gran apoyo en la resolución de ecuaciones diferenciales: de constante aparición en modelos físicos, matemáticos, financieros o biomédicos. Por ejemplo, el átomo de hidrógeno es representado por el grupo de simetrías SO(4).

Otro ejemplo importante en la Mecánica Cuántica es la invarianza de las funciones de ondas bajo el grupo de simetrías U(1), es decir, las funciones de onda desencadenan la misma fenomenología física aunque presenten un cambio de fase tipo e^iα.

El enunciado anterior puede comprobarse trivialmente hallando la densidad de probabilidad P de que una partícula se encuentre inmersa en una región del espacio. El cálculo se realiza de la siguiente forma:

donde Φ es la función de onda en un espacio de Hilbert H, Φ^*es su conjugada compleja y dr es el diferencial de volumen. Está claro la densidad de probabilidad es invariante bajo transformaciones Φ –> e^iα Φ, siempre que se encuentren combinaciones de la función de onda y su complejo conjugada.

Una de las disciplinas científicas más famosas por el uso de la teoría de grupos es la física de partículas. En 1969, el físico estadounidense Gell-mann predijo la existencia la partícula Ω, una pieza fundamental en el incompleto modelo de SU(3) de sabor.

Acostumbrados a la intuición física, este caso supuso un claro ejemplo de intuición matemática, lejana a las evidencias experimentales (probadas cuatro años después del postulado de existencia, en el laboratorio de física de partículas de Brookhaven).

Hasta el momento, las cuatro interacciones fundamentales en la naturaleza (interacción fuerte, débil, electromagnética y gravitatoria) habían sugerido la existencia de familias de partículas con una serie de propiedades. Dependiendo de su interacción, se hizo una primera clasificación en leptones y hadrones, aquellas que no interactúan “fuerte” (transparentes a esta interacción) y las que sí, respectivamente. Los componentes fundamentales de los hadrones se denominan quarks.

Dentro de los hadrones, se hizo una primera clasificación atendiendo al spin, cualidad de las partículas que se manifiesta en la presencia de campos electromagnéticos (recordatorio: si las partículas tienen spin semientero se denominan fermiones y si es entero, son bosones), y una segunda subclasificación dentro de los posibles spines enteros y semienteros: la representación de las partículas atendiendo a su spin isotópico o isospín. El isospin es otra propiedad intrínseca de las partículas, dependiente de su contenido quark. Las partículas fundamentales contempladas por grupo de simetrías global SU(3) sabor están compuestas principalmente por los tres quarks más ligeros u, d y s, que son los denominados sabores. Así, los hadrones se denominarán bariones si contienen tres quarks o mesones si contienen un quark y un antiquark. Existen partículas exóticas que no siguen estas reglas de contenido quark.

La genial idea de Gell-Mann fue hacer las representaciones irreducibles de SU(3) sabor atendiendo al spin de los fermiones más ligeros (1/2) y su primera excitación, con spin 3/2) y los bosones más ligeros (con spin 0 y su primeras excitaciones, con spin 1). Si se representa cada partícula con las mencionadas propiedades en unos ejes coordenados en los que se representan la proyección de isospín y la hipercarga (magnitud física que combina el número bariónico y la propiedad extrañeza), se obtienen los diagramas a continuación. Notar que I₃ o T₃ es la mencionada proyección de isospin e Y representa la hipercarga.

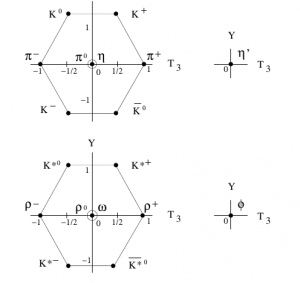
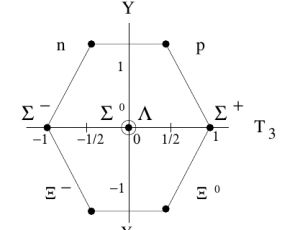
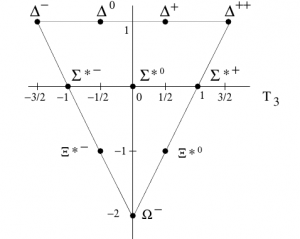
El resultado fue los octetes (a pesar de ser hexágonos existen dos partículas en el centro, de ahí que sea un octete) representaban las propiedades físicas de las partículas conocidas. En el caso del decuplete (o sea, el triángulo), las partículas señaladas eran conocidas excepto la Ω situada en el pico. Esta representación pictórica de una idea abstracta matemática, fue la que indicó que debería existir otra partícula que completara el decuplete. Y así fue como, posteriormente, el modelo SU(3) sabor pudo completarse adecuadamente.

No obstante, en los últimos tiempos, parece que el modelo estándar se tambalea, debido a la existencia de teorías superiores y que poco a poco, podrán corroborarse experimentalmente debido a la infrastructura que estamos construyendo, como el acelerador-detector LHC (Large Hadron Collider). Sin embargo, otra pieza clave del puzzle fue corroborada en 4 de Julio del 2012, en la que se probaba la existencia del bosón de Higgs, o partícula encargada de la dotación de masa de las partículas del modelo estándard. Este descubrimiento reafirmó la base teórica del modelo estándard, sin embargo, los experimentos posteriores, aún no anunciados oficialmente, parecen apuntar la existencia de más de un bosón de Higgs, lo que de nuevo, nos llevaría a una redefinición del modelo estándard. No obstante, a día de hoy, el modelo estándar sigue presentándose como el modelo de grupo de simetrías gauge SU(2) × SU(3) × U(1), que se corresponden, respectivamente, con los grupos asociados al isospin débil, color (otra propiedad de las partículas interactuando en un campo fuerte) y la hipercarga débil. Sin embargo, el grupo gauge no tiene cabida en este breve comentario de cómo la teoría de grupos, una teoría matemática estrictamente abstracta, contibuyó en la predicción de un modelo físico.

Quepa esta anotación teórico-histórica para convencer a matemáticos recalcitrantes, que la aplicación de una teoría matemática al mundo que nos rodea, puede conducirnos a resultados excepcionales, más allá de lo esperado, que no sólo existe la belleza en un enunciado formal, autocontenido y lógico, sino que la naturaleza es caprichosa y nos brinda muchos secretos que aún hemos de descubrir.

____________

Christina Sardón, Salamanca