La engañosa humildad del triángulo

Reflexionamos en esta entrada sobre unos objetos geométricos a los que a veces no les damos la importancia debida, los triángulos.

Todos sabemos lo que es un triángulo, la figura plana mas sencilla: tres lados, tres ángulos, tres vértices, abarcando un trozo definido del plano. Todos los demás polígonos se pueden descomponer en triángulos, así que estos son los ladrillos de la geometría plana (este proceso se llama triangulación). El número mínimo de triángulos necesarios para esta división es n-2, donde n es el número de lados del polígono. Por eso los triángulos fueron objeto de un estudio intensivo en “Los elementos” de Euclides, que les dedicó su Libro I.

Y recordamos, cómo no, la clasificación del colegio: equiláteros (“lados iguales”), isósceles (que significa “piernas iguales”) y escalenos (del griego “desigual”). Y los podemos clasificar también por sus ángulos, rectángulos, obtusángulos y acutángulos, porque un famoso teorema establece que la suma de los tres ángulos de un triángulo es siempre 180º (esto ya lo demostró Euclides).

Esta noción de triángulo plano se puede extender a cualquier superficie, y en dimensiones arbitrarias, a espacios mas generales, las llamadas variedades diferenciables. En este caso, necesitamos extender el concepto de recta al de línea geodésica y nos encontramos con lo que llamamos un triángulo geodésico, cuyos lados son segementos de geodésicas.

Aquí ya no nos vale que la suma de los ángulos interiores es 180º, y la diferencia mide el exceso o defecto debido a la curvatura, por ejemplo en el caso de triángulos esféricos o triángulos en el plano hiperbólico o de Lobachevskii. Recordemos que las geometrías no euclidianas surgen cuando nos olvidamos del quinto postulado de Euclides (por un punto exterior a una recta pasa una sola paralela) y admitimos que no pase ninguna (geometría esférica) o infinitas (geometría hiperbólica). Este gran logro del pensamiento que permitió a Albert Einstein desarrollar la teoría de la relatividad se refleja como decíamos en las propiedades de los modestos triángulos.

Una aventura que tiene como protagonistas a los triángulos es precisamente la medida del meridiano, con nombres como Maupertuis y La Condamine (y los españoles Jorge Juan y Antonio de Ulloa) basada en las triangulaciones. Algo parecido a lo que ahora hacen nuestros GPS orientándonos cuando nos desplazamos por la superficie de nuestro planeta.

Los triángulos son pues mas importantes de lo que pareciera en una primera impresión, y por eso sus propiedades nos importan. Y son muchas, dando lugar a puntos notables, como el baricentro o centroide (punto de intersección de las medianas, un auténtico centro de gravedad), circuncentro (intersección de las mediatrices de los lados), incentro (intersección de las bisectrices de los ángulos), y ortocentro (intersección de las alturas).

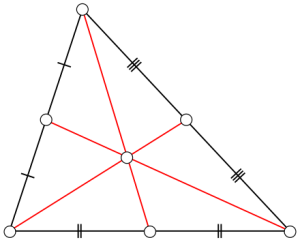
Y estos puntos tienen otras propiedades; el circuncentro es el centro de la circunferencia circunscrita que pasa por los tres vértices del triángulo; y el incentro es el centro de la circunferencia inscrita, que es tangente a los lados del triángulo.

¿Y qué decir de la maravillosa fórmula de Herón que relaciona el área de un triángulo con su perímetro? ¿O del teorema de Pitágoras para los triángulos rectángulos? ¿O de las relaciones trigonométricas?

Contaremos en futuras entradas mas maravillas sobre los triángulos, y seguramente ya no nos parecerán tan modestos como al principio.

—

Manuel de León (CSIC, Fundador del ICMAT, Real Academia de Ciencias, Real Academia Canaria de Ciencias, ICSU)