Triángulos de Heron
Estos últimos meses me he dedicado a leer muchos artículos sobre unos falsamente modestos objetos geométricos, los triángulos. Fruto de esa curiosidad, traemos a Matemáticas y sus fronteras un tipo de triángulos con propiedades muy interesantes, los llamados triángulos de Heron.
Un triángulo de Heron es áquel cuyos lados y áreas son números enteros. Fácilmente vemos que cualquier triángulo rectángulo con lados enteros es de Heron, porque el área es la mitad del producto de los dos catetos, ya que uno actúa como base y el otro como altura:
Un ejemplo de un triángulo heroniano que no es rectángulo es uno isósceles que se puede obtener pegando dos triángulos rectángulos de lados 3, 4, y 5 por el cateto de longitud 4; así obtenemos un triángulo isósceles con lasdos de longitudes 5, 5 y 6, y área 12 unidades cuadradas.
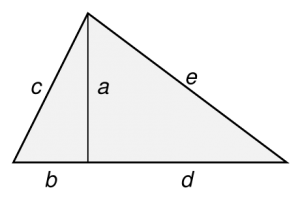Esta técnica vale en general, porque si tomamos un triple pitagórico (que es equivalente a dar un triángulo rectángulo) (a, b, c), con c mayor que a y b, y tra (a, d, e), con e mayor que a y d, entonces podemos construir un nuevo triángulo pegando los lados de longitud a (veáse la figura anterior).
Las longitudes de sus lados serán c, e, y b + d, y el área es A = 1/2 (b+d) a
En consecuencia, si a es un entero par o b+d lo son, entonces el área A es entera.
Pero no todos los triángulos heronianos son así, y se llaman indescomponibles. Podemos permitir una generalización del concepto de triángulo heroniano permitiendo que los lados y el área sean números racionales. En este caso, siempre se puede hacer esa descomposición.
Heron encontró una fórmula maravillosa que relacionaba el área con el perímetro de un triángulo
dónde a, b, y c son las longitudes de los lados y s es el semiperímetro. Por lo tanto, tenemos una ecuación diofántica
El conjunto completo de soluciones para triángulos heronianos fue encontrada (¡cómo no!) por Leonhard Euler, y las versiones paramétricas son debidas a Brahmagupta y Carmichael (1952), y son de este tipo
para los valores de a, b, c, s y Δ, respectivamente. Aquí, los enteros m,n y k verifican
Así se pueden producir infinidad de triángulos de Heron de una manera sencilla.
La curiosidad sobre los problemas matemáticos es inagotables, y así nos encontramos con tetaedros heronianos y pirámides perfectas.
¡Un mundo apasionante el de los triángulos!
____
Manuel de León (CSIC, Fundador del ICMAT, Real Academia de Ciencias, Real Academia Canaria de Ciencias, ICSU).
[…] Triángulos de Heron | Matemáticas y sus fronteras Compártelo:FacebookGoogleTwitterLinkedInRedditSkypeTumblrWhatsAppTelegramCorreo […]
Businesses from around the world have integrated communication tools to speed up their exchange of information with employees or customers. The smartest tool they can use is a SMS gateway which connects their system with a texting service to send real-time messages.
We hear about different product launches every day but often miss out on some great deals. Businesses are aware of this so this is why they use text blasts for promotion of new products and services to their dedicated audiences.