![]()
Suelos de México: Distribución de Abundancia y Curva de Willis
Como ya os comentamos, la distribución de los suelos en un espacio geográfico concreto se ajusta a la denominada Curva de Willis. Tal curva nos informa que unos pocos tipos de suelos o edafotaxa son muy abundantes, mientras que la mayoría solo ocupan escasas extensiones de terreno. Se trata de un patrón muy ubicuo que, a menudo es síntoma de estructuras fractales o multifractales subyacentes (ver post incluidos en la categoría “Diversidad, Complejidad y Fractales”). Hasta la fecha he mostrado en varios post tales estructuras con datos propios. Hoy lo haré con los que en su día os proporcionaron Carlos Cruz y colaboradores para el territorio Mexicano, utilizando la clasificación más reciente de la FAO (WRB 2006). Como veréis seguidamente, la distribución de los suelos conforme a su abundancia en México se ajusta perfectamente a este patrón.
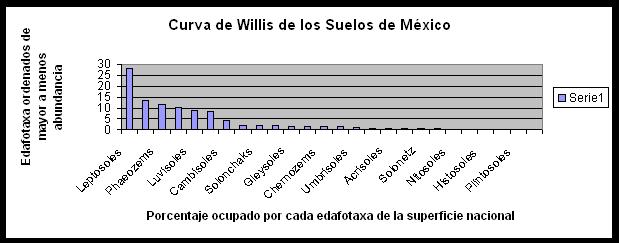
Curva de Willis de los suelos de México
En la categoría “Geografía de Suelos y Megaedafología” se encuentran los datos originales de uno de los post escrito por Carlos Cruz, Claudio Balbontin, Fernando Paz, Jorge Etchevers y Pavel Krasilnikov, así como otros post acerca de los suelos de este país. No se conocen muy bien las razones de la obicuidad de la curva de Wilis, que por ciento también aparece en los inventarios de biodiversidad y las estructuras taxonómicas. Imaginaros una tartea que la dividimos en porciones de diferentes tamaños. Pues bien, siempre unas pocas son enormes y la mayoría muy pequeñas. Su número crece conforme disminuye su tamaño. Desgraciadamente, ocurre lo mismo con la distribución de la riqueza.: Muy pocos multimillonarios, más ciudadanos de la clase media y una enorme plétora de personas en la popreza o en el umbral de la misma. Este tipo de distribuciones fueron redescubiertas muy recientemente y son denominadas de colas crasas o de colas largas. ¿Porqué nadie se acuerda de Willis?, que ya detectó tal patrón en 1992. Sinceramente no lo sé y se me antoja que es una gran injusticia. Los canones de la buena ciencia dictan que se recuerde a su primer descubridor. Sin embargo, al parecer, los sacerdotes actuales de la ciencia, o bien leen muy poco, o se saltan a la torera la ortrdoxia que dicen defender.
Como os hemos comentado, suele ser usual que bajo tales distribuciones subyazcan estructuras fractales o multifractales. La mejor manera de saberlo es analizar si los datos se ajustan a una distribución potencial. Ya hemos abundado sobre este tema en numerosos post incluidos en la categoría de “Diversidad, Complejidad y Fractales”. Básicamente, si los datos son trasformados a logaritmos (da igual la base que se utilice, neperiana, 2, 10, etc) y los ordenamos de la misma forma que lo hicimos para la curva de Willis, en coordenadas cartesianas se ajustan a una línea recta. Veamos lo que ocurre en el caso de los suelos de México.
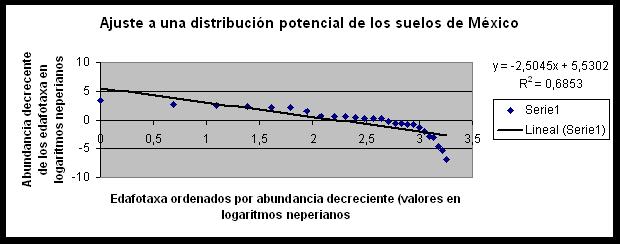
Ajuste a una potencial de los suelos de México al
ordenarlos en función decreciente de la extensión que ocupan
Como podéis observar, los datos se ajustan bastante bien excepto (mayor del 95,5% de probabilidad) en el extremo izquierdo de la curva. ¿Qué significa este hecho? Simplemente que existen unos pocos tipos de suelos que cubren extensiones casi insignificantes a nivel nacional que son todavía más abundantes de lo que cabría esperar para una potencial (aun una mayor pobreza de la esperada, si nos atenemos a la metáfora de la riqueza). Se trata también de otro patrón bastante ubicuo que nos viene a decir que si bien la distribución de los edafotaxa conforme a su tamaño tiende a ajustarse a una ley potencial (invariante a los cambios de escala), se presentan ciertas anomalías que requieren el auxilio de herramientas multifractales con vistas a obtener una caracterización mucho más precisa. Bajo estas circunstancias, existe una distribución estadística llamada de Weibull (ver este, este, este y este post) que suele ajustarse mejor a los datos que una potencial. Nosotros ya publicamos este hecho, aunque no ha hado lugar a mayores indagaciones hasta la fecha. Tal hecho nos ocurrió al analizar por ejemplo la estructura matemática de la taxonomía americana de suelos.
Pues bien, ya sabéis que en cualquier espacio geográfico, tanto si analizáis la biodiversidad de especies o la edafodiversidad, con casi total seguridad os aparecerá una Curva de Willis.
Juan José Ibáñez

[…] ley (por ejemplo frecuencia-tamaño de las cuencas de drenaje, magnitud-frecuencia de terremotos, extensión ocupada por los tipos de suelos o edafotaxa en un determinado territorio, etc. etc.). Y de este modo parece habarse dado un paso […]