![]()
Transmisión de la información, Conectividad y Redes Sociales: El Número Mágico 6 o ¿7?
En nuestros últimos post: “Conectividad, Redes Sociales y Redes Ecológicas” y “Redes Complejas: Redes Sociales y Redes Ecológicas (Los Mundos Pequeños)” hemos venido hablando de las redes complejas y sus estructuras. Demostramos como las redes sociales de Internet, las redes ecológicas de todo tipo, los constructos tecnológicos, etc., siguen el mismo patrón de autoorganización. Lo mismo podríamos indicar sobre las rutas metabólicas. Hoy nos centraremos en un ejemplo de Internet. Se trata de una vieja noticia de 2005 que apareció en el rotativo ABC y que llevaba por título: Internet una cadena con pocos eslabones. Hablaremos pues de la transmisión de información, sociabilidad y contagio epidémico, etc. en redes complejas. Como ya os hemos comentado en los post previamente escritos, tales sistemas se ajustan a unas configuraciones denominadas de “los mundos pequeños”. No obstante, antes de comenzar conviene recordar una crítica que ya he leído varias veces en el mundo académico en contra de los expertos en ciencias de la computación.

Small Worlds. Kandisnky. National Gallery of Australia
Son varios los expertos en ciencias de la computación que se quejan de que muchos de sus colegas redescubren la dinamita al encontrar patrones en la estructura de la Web que dan por nuevos, cuando en realidad fueron detectados mucho antes del advenimiento de la era de Internet. Tal hecho está generando muchas confusiones en la bibliografía, y es a todas luces reprochable. Se trata de un asunto lo suficientemente serio como para que lo tratemos debidamente en otra contribución. Digamos que el texto que os exponemos seguidamente adolece de este serio defecto, como se verá en otros comentarios posteriores más abajo. Vayamos pues con la noticia.
Mundos pequeños: entre el orden absoluto y el caos total
Internet, una cadena con pocos eslabones
VÍCTOR M. OSORIO/14-9-2005 10:54:26
A menudo pensamos que internet es un mundo enorme, un mastodonte imposible de abarcar. ¿Pero es así o no? Un estudio de un equipo de investigadores del Instituto Tecnológico de Massachusetts y del Instituto Carleton (EE.UU.), publicado en el periódico de la Academia Nacional de las Ciencias de Estados Unidos, parece desmontar la teoría de la «inmensidad de internet». La conclusión del trabajo tiene nombre de película: «Seis grados de separación». Y es que han mostrado cómo dos internautas pueden encontrar una conexión entre ambos en pocos pasos. Concretamente en seis.
Su experimento ha tomado como muestra una comunidad «on line» estadounidense denominada Livejournal.com. En ella 500.000 «bloggers» tienen puesta su localización geográfica y los «links» de sus amigos. El objetivo fue analizar cuántos pasos eran necesarios para que un mensaje alcanzase una ciudad elegida como objetivo a través de los contactos de un emisor cualquiera. Los sociólogos vieron que una persona puede transmitir un mensaje a cualquier otra que no conoce a través de una pequeña cadena de amigos que actúen de intermediarios. Además, han encontrado un modelo matemático que explica este fenómeno.
Extrapolando los resultados a todo Internet, la conclusión es que, en sólo seis pasos (seis intermediarios), existe una enorme probabilidad de que cualquiera pueda recibir un mensaje nuestro. ¿Cómo? Una persona se lo manda a sus conocidos, estos a todos sus conocidos y así hasta seis veces. En la cadena que se va construyendo, en forma de árbol y que va creciendo de forma exponencial, al final hay un camino por el que el mensaje puede llegar a una persona elegida al azar que se encuentre en cualquier lugar. El resto de caminos se irán cerrando a medida que vayan aumentando los pasos, pero la probabilidad de que llegue el mensaje por una de las sendas que se tejen, sería tan elevada que un séptimo intermediario resulta mucho menos importante en términos estadísticos.
Con seis pasos, los investigadores afirman que la cadena se completa en el 80 por ciento de los casos. No obstante, advierten de que la seguridad no puede alcanzar nunca el cien por cien, salvo con pasos infinitos, puesto que la cadena siempre puede fallar porque llegue a una persona que no la continúa y que se convierta en el fin de la misma.

Redes topológicas aleatorias, muy diferentes
a las de los mundos pequeños
La distancia sí importa
El estudio también concluye que la probabilidad de ser amigo de alguien disminuye a medida que aumenta la distancia entre ambos. De hecho, dos tercios de las relaciones de amistad que fueron analizadas estaban influenciadas por la localización geográfica de las personas. En concreto, son la localización y la ocupación laboral las dos dimensiones que más influyen para averiguar el siguiente paso de la cadena que seguirá un mensaje enviado. Y en los primeros pasos, la clave es la distancia, que explica el 70 por ciento de las relaciones de amistad en Internet.
Pero no todo es tan fácil. Resulta que esta tendencia también depende de la densidad de población que exista entre las dos personas. Un ejemplo: dos leoneses tienen más probabilidad de ser amigos viviendo a veinte kilómetros de distancia que dos madrileños.
Internet, la red de redes, con millones de direcciones Web y con posibilidades casi infinitas, aparece tras este estudio en algo más fácil de aprehender en lo que a relaciones entre personas se refiere. Las mismas tecnologías que ponen distancia de por medio entre las personas, se muestran ahora como un medio a través del que pueden estar más unidas que nunca.
Recordemos la cadena de seis. Ya hablaremos de ella más abajo. Tan solo haceros ver por el momento, como el proceso detallado genera una jerarquía concreta en un mar de nodos que no se ajustan a tal estructura. Como ya comentamos en otro post, los sistemas jerárquicos son óptimos con vistas a transmitir el flujo de materia, energía e información de la manara más eficiente y rápida posible (a pesar de la opinión de muchos amantes del ciberespacio). Veamos ahora lo que se nos dice en este enlace:
Teniendo en consideración que los investigadores conocen a otros investigadores, cada uno de ellos puede ocupar el puesto de un eslabón en una «cadena», la cual no distaría más de seis eslabones para poder unir a todos los autores de la psicología norteamericana. Esta es la propuesta que hacemos al tratar de conectar a todos los autores más productivos mediante los nexos de unión más cortos y que más autores engloben.

Semejanza entre la estructura cerebral y cósmica
Reiteramos que, como ya mostramos en post anteriores, pensar que todos los patrones que se detectan en la Web son novedades, es como defender que la filosofía contemporánea soslaya las lecciones de los clásicos helénicos. Tremenda incultura de la que jamás debe hacer gala un científico. Pero como muchos distan años luz de pretender ilustrarse (basta con aparentar), luego pasa lo que pasa. Veamos ahora en este enlace un testimonio más de como los investigadores de Internet redescubren la dinamita con harta frecuencia. Pero eso sí, este documento es mucho más serio que el anterior, a pesar de que el estudio se llevó a cabo por investigadores del mítico MIT. El antecedente es de 1967, décadas antes del imperio de la WWW.
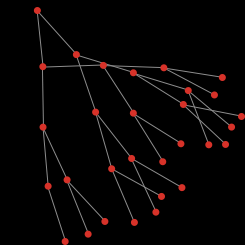
Sistema Jerarquico de seis pasos
Un día, lejos de nuestra ciudad, tomamos un tren y comenzamos a conversar con el pasajero del asiento de al lado. La conversación se anima, se pasa de las generalidades al relato de los propios mundos de cada cual y en un momento descubrimos conocidos comunes… y es que «el mundo es un pañuelo«, o como se diría en inglés «what a small world it is». En 1967 el controvertido psicólogo social Stanley Milgram realizó un experimento original: seleccionó cincuenta personas a las que entregó un mensaje para un único destinatario. El mensaje sólo podía ser entregado a un conocido o, por estos, a otro conocido, hasta alcanzar el objetivo final. El experimento no salió muy bien las primeras veces, con una tasa de recepción final del 5% (cosa que no impidió a Milgram publicar los resultados y abrir un debate que ha sido sumamente fértil). En sucesivos intentos la tasa de recepción se elevó incluso hasta el 97%. Poco a poco una idea emergió de los experimentos, la de los seis grados de separación: cualquier persona podría llegar a cualquier otra siguiendo tan sólo seis pasos de «amigos de amigos» (en ingles «friend of a friend» o FOAF).

Stanley Milgram. Fuente: Google images
¿Sorprendente? Si aplicásemos la lógica de la venta piramidal no debía de serlo. ¿Quién no conoce a cien personas? Si cada una de ella conociera a otras cien (distintas), en dos grados podría llegar a 10.000 personas y en seis grados a más de 9000 millones, lo que es bastante más de la población mundial. (….)
Este fenómeno se llama clustering y podríamos definirlo como la tendencia que tienen dos conocidos comunes a un tercero a conocerse entre si. O dicho a la manera del análisis de grafos, la tendencia a que dos nodos conectados a través de un tercero se conecten directamente entre si.
El clustering hace que la gran red social se parezca más a una red de redes que a una única red muy interconectada. En el mundo pequeño anterior a Internet, la red social sería una red descentralizada. En el lenguaje del análisis estructural diríamos que la red social real tendería representarse como un conjunto de «clusters» unidos entre si por puentes locales. Son estos puentes los que permiten que sólo haya seis grados de separación media en una red social amplia dándonos la impresión de que «el mundo es un pañuelo» (el Small World Phenomenon).
Permítanme un inciso. Las últimas líneas hacen referencia a la configuración de mundos pequeños, de la que ya hablamos en nuestro post anterior: “Redes Complejas: Redes Sociales y Redes Ecológicas (Los Mundos Pequeños)”. Pero sigamos con la narración interrumpida.
Claro que para que los puentes reduzcan tanto el número de grados de separación medio en grandes poblaciones hace falta algo más que su existencia. Los puentes garantizan la existencia de uno o más caminos entre dos nodos, no que los caminos geodésicos tengan pocos grados. Para eso hacen falta que los nodos de los que surgen los puentes sean verdaderos conectores («hubs»), que estén muy conectados con distintos clusters y conectados entre si. Dicho de otro modo, los conectores son nodos de fácil acceso desde distintas subredes. (..)
Evidentemente esto es así en redes de contactos, en las redes de afinidad entre bloggers, etc. Pero no tanto en otras redes como las formadas por contagio de ciertas enfermedades.
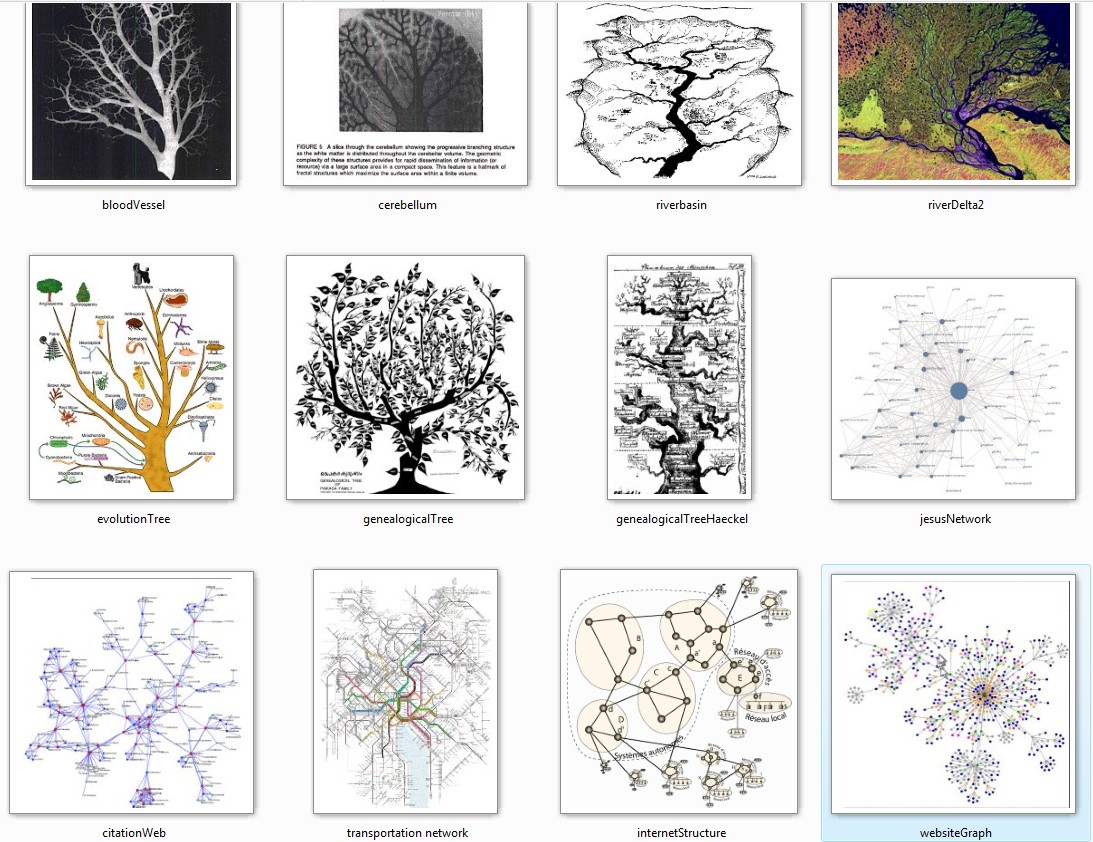
Multiples ejemplos de mundos pequeños: citaciones de
un artículo, visitas de un sitio Web, diversas estructuras
naturales. Fuente: Bordalier Institute
A pesar de lo que dice el autor, en su momento leí artículos sobre epidemiología que hacían referencia a los seis eslabones. Es una lástima que no pudiera rescatar alguna de las referencias. También se habla de la regla de los seis pasos en el siguiente enlace de Wikipedia, o en este otro. Más aun, aquí se nos informa de nuevo, tomando como punto de partida el marketing viral de que:
La teoría de las redes, que estudia los resultados de modelos con distintos «nodos» que se relacionan entre sí, tuvo un avance resonante en la década del 60, cuando el psicólogo social de Harvard Stanley Milgram demostró que seis pasos suelen ser suficientes para conectar a una persona con cualquier otro desconocido en el mundo, a partir de relaciones comunes. La hipótesis fue luego demostrada matemáticamente y popularizada con el juego «Six degrees to Kevin Bacon», en el cual hay que llegar en menos de seis pasos al actor.
Pero retornemos una vez más al enlace del blog de Augusto de Franco en el que se abunda mucho más sobre la conjetura de los seis pasos: y la propia conectividad. Esta blogger también vuelve a incidir sobre las propiedades las redes de mundos pequeños respecto a las aleatorias, en lo que a su conectividad y resistencia a las perturbaciones concierne. En consecuencia, os copiaré un texto amplio, no sin antes indicaros que su descripción es mucho más profusa y rica, por lo que os conmino a que la leáis en toda su integridad en deugarte.com Contextos.
¿Cómo se percata Watts de que tal cuestión está en el núcleo de esta historia? Básicamente describiendo el experimento de Stanley Milgram, realizado en 1967 y que hasta el día de hoy sigue siendo una referencia central en las ciencias sociales. Lo que Milgram demuestra es que, como máximo, necesitamos cerca de seis pasos para conectarnos con cualquier persona en el planeta. Aunque suene increíble y contra-intuitivo las cosas son así y esto pone de manifiesto el alto grado de «clusterización» (clustering) o agrupamiento que gobierna al mundo social. La clusterización implica que, por supuesto, todos no conocemos a todos, pero vinculando adecuadamente a los diferentes grupos en que nos movemos podemos llegar a contactar a cualquiera.
A continuación se despliega una perspectiva introductoria del trabajo de Erdös y Renyi, dos matemáticos húngaros que inventaron la teoría de grafos aleatorios (random graphs) a principios del siglo XX.
Uno de los descubrimientos más significativos de estos investigadores es que en un grafo aleatorio la conectividad aumenta dramáticamente al incorporar más nodos al componente central de una red. Tal conectividad global, según Erdös y Renyi, no se desarrolla incrementalmente y de manera regular, sino que crece incontrolablemente después que se ha sobrepasado determinado umbral. A pesar de la enorme utilidad de esta teoría para dar cuenta de la topología factual de muchas redes, en el mundo real Watts descubre que otras no tienen tal forma aleatoria en la que la distribución de la conectividad se ajusta a la figura de una campana de Gauss. (…)
Un inciso antes de continuar, como ya hablamos en los dos post anteriores, es decir en los enlazados al inicio de este, la estructura de Internet, como el de las redes biológicas dista mucho de ser aleatoria, siguiendo el denominado diseño de los mundos pequeños. Que yo sepa, en estas últimas la conectividad no aumenta tan súbitamente al añadirse nuevos nodos al entramado de Internet. Y esta discordancia la genera las propiedades de las configuraciones de los mundos pequeños. Pero continuemos.
Redes sociales, redes biológicas, redes tecnológicas
(…) También podemos decir que la dinámica del propio entramado – el otro factor crucial – puede ser vista desde otras posiciones. Podemos hablar de dinámica de la red (como se desarrolla su estructura) o de dinámica sobre la red, que es el producto generado por una red particular y más allá de su estructura. En las redes reales, por supuesto, ambas dinámicas están fuertemente vinculadas («la felicidad afecta a la red y al red afecta a la felicidad»).
En términos de reseñar contribuciones teóricas Watts retoma entre otros el aporte de los físicos, quienes utilizaron el concepto de transición de fase como clave para comprender el modo en que un súbito aumento de la conectividad implica una transformación fundamental en cualquier sistema empírico. Esta propiedad es conocida como «universalidad» y está vinculada a la posibilidad de observar los mismos desempeños en distintos ámbitos fácticos (..).
Las redes de pequeño mundo (small-world networks) representan una instancia intermedia entre ambos extremos e inevitablemente existen en las situaciones en las que el promedio de longitud de pasos entre nodos es pequeño y el coeficiente de clustering es importante. En este estado transicional las regiones de la red están vinculadas por atajos (shortcuts) que vinculan a todos los nodos.
En 1997 una fraternidad universitaria inventó un desafío que sirvió para construir el llamado «Juego de Kevin Bacon«, que consiste en demostrar que este actor es el «centro» del universo fílmico a través de un simple proceso de mapeo de la conectividad del mundo de Hollywood. El resultado de este experimento es contundente: en un mundo formado por cientos de miles de individuos, cada actor está conectado con cualquier otro en un promedio de 4 pasos.
Watts y el matemático Steve Strogatz, a partir de estos indicios, rastrean otras redes con similares características y llegan a conclusiones idénticas. Tanto en fenómenos biológicos como en infraestructuras artificiales, y hasta en el mismo universo de Internet, las propiedades de las redes de pequeños mundos parecen estar presentes.
Luego se explica en detalle el modo en que las redes libres de escala o de mundo pequeño se diferencian de las distribuciones gaussianas o de Poisson. Siguiendo a la ley de Potencia formulada por Wilfredo Pareto en el siglo XIX, las redes que tienen la forma y las particularidades de las distribuciones libres de escala se diferencian enormemente de aquellos fenómenos que pueden ser descriptos con el desarrollo de una curva normal.
En primer lugar, las distribuciones de este tipo no tienen un pico que corresponda con su valor promedio y, en segunda instancia, comienzan con un valor máximo y decrecen lentamente hacia el infinito. Watts presenta la distribución de alturas de una población como caso típico que toma la forma de una curva normal y, como situación antagónica, la relación que puede establecerse entre la población de una ciudad grande y un pequeño villorrio. Esas diferencias extremas son inconcebibles en una distribución de Poisson, pero se encuentran en muchos más fenómenos que los previstos por Watts y Strogatz. Al parecer la estructura física y virtual de Internet, por ejemplo, tiene esta forma, y lo mismo puede decirse de las redes metabólicas de muchos organismos biológicos.
Sin embargo los descubrimientos de estos investigadores van más allá de esta corroboración porque además postulan un mecanismo elegante por el cual estas redes pueden evolucionar en el tiempo. En efecto, en redes con una distribución inequitativa de cualquier recurso el interrogante capital seguramente apuntaría a dilucidar los probables motivos de ese resultado final. Los autores apelan aquí al difundido «efecto San Mateo» traído al ámbito de las ciencias sociales por el renombrado sociólogo norteamericano Robert K. Merton. Este fenómeno, sustentado en aquel pasaje bíblico que plantea que todo lo que tenemos en muestra vida terrenal nos será dado en abundancia en el cielo y todo aquello que poseemos en carácter de escaso nos será retaceado aún más, parecería ser exactamente el tipo de proceso que rige la ampliación de las diferencias de cualquier tipo que los nodos de distintas redes parecen mostrar a largo plazo en las distribuciones libres de escala. Así, aplicando este principio al ámbito estrictamente económico, aquellos individuos que poseen riqueza se vuelven aún más ricos con sorprendente facilidad, y aquellos que permanecen en la pobreza no solo no pueden salir de su condición aunque lo intenten, sino que es probable que se vuelvan aún más pobres en el futuro.
En sintonía con esta audaz comprobación son introducidos los comentarios de la obra de Bárabási y Albert, dos matemáticos de origen húngaro que tuvieron el acierto de postular el mecanismo por el cual este tipo de redes pueden configurarse como libres de escala de acuerdo a un principio no igualitario de acumulación de relaciones. Si pensamos en redes sociales en las cuales de entrada contamos con una cantidad diferencial de relaciones y tratamos de establecer una pauta de crecimiento realista de los contactos caeremos en la cuenta de que aquellos nodos que se agreguen a la red en cada momento específico muy probablemente lo hagan tratando de conectarse con aquellos nodos mejor relacionados. Este fenómeno es denominado por Bárabási y Albert como «enlace preferencial» (preferential attachment) y se puede decir que es la piedra de toque procesual de las redes libres de escala.
En tiempos más o menos contemporáneos a los de Bárabási (exactamente en 1955) el Premio Nobel Herbert Simon, inventor del concepto de «racionalidad con límites» (bounded rationality) utilizó un modelo muy similar a este para explicar el tamaño desigual en las firmas comerciales, y el profesor de Harvard George Kingsley Zipf postuló en momentos tan tempranos como 1949 la famosa ley que lleva su apellido al describir la frecuencia muy desigual con la que aparecen las palabras en el idioma inglés. Estas distribuciones inequitativas tienen el exacto sello de las redes libres de escala.
Sin embargo algo interesante es que el libro trata de realizar en todo momento una apropiación crítica de los enfoques que se comentan. En este sentido Watts da testimonio de una comprobación poco auspiciosa: según sus comentarios la psicóloga Judith Kleinfeld, en un escrutinio profundo del experimento de Milgram, fue la encargada de descubrir que las cosas no funcionaban exactamente como el autor del experimento declamaba. En primer lugar, y bien analizados los datos de base, solamente unas 96 personas de las 300 incluidas en el experimento cumplen las condiciones de selección aleatoria y residencia descriptas por Milgram. De esas 96, solo 18 cumplieron con el objetivo de la consigna en los términos de los 6 grados postulados por los defensores de la experiencia. El contraataque epistemológico de Watts es muy aleccionador, ya que argumenta que, si bien las cartas del experimento de Milgram fueron conducidas a sus destinatarios en una modalidad de contacto directo y sin saturar la red (direct mode), el contacto podría haberse buscado usando una vía mucho más pesada y ciega al contexto (broadcast mode) pero logrando resultados mucho más efectivos.
Creemos que una de las cosas notables de esta parte del trabajo, más allá del relato que Watts hace de como el problema de Milgram fue abordado por sucesivos investigadores, es que la resolución de problemas científicos no es delegada a un selecto grupo de iluminados y no opera conclusivamente en el tiempo de acuerdo a la narración interesada de algunos de sus protagonistas directos. Es decir, la evolución de una idea nunca puede darse por terminada.
Un nuevo inciso. Redes libres de escala se refiere a la existencia de estructuras potenciales (entendidas aquí como la Ley de Zipf) y posiblemente de estructuras fractales subyacentes. Del mismo modo, la Ley de San Mateo nos retorna a la ya archicomentada, en otros post, curva de Willis. Pero sigamos indagando que nos dice Augusto Franco en su bitácora.
Epidemias y resistencia
Luego y sin que medien demasiadas transiciones el centro de atención pasa a ser los procesos epidémicos de orden sanitario. De la difusión de la riqueza, de los contactos o de las fallas de un sistema artificial como Internet pasamos a la letal difusión de epidemias, y Watts vuelca todo su repertorio conceptual en el ataque a esta cuestión.
En primera instancia describe al brote de Ebola del año 2000 como un ataque que no alcanzó a transformarse en epidemia por el mismo modus operandi letal del virus. En efecto, su tasa de mortalidad es tan elevada y su tiempo de acción tan escaso que no ofrece tiempo para que sus víctimas se desplacen a centros urbanos poblados e infecten a una masa demográfica mayor. Sin embargo la difusión planetaria de virus como el HIV, de etiología prolongada y acción más gradual, supone un nuevo tipo de desafíos al combinarse con las tecnologías de transporte del siglo XXI, ya que las víctimas expanden dramáticamente su rango de acción y pueden llegar a contagiar a personas al otro lado del mundo con absoluta facilidad. ¿Cómo pueden comprenderse estos procesos de expansión epidémica con el auxilio de la teoría de las redes de mundo pequeño? Diversos atributos, y no sólo un rasgo, parecen ser entonces la clave para la comprensión de la tasa de expansión y éxito de los virus biológicos. Algo similar puede decirse de la difusión de virus artificiales en Internet.
¿Mediante qué mecanismos y condiciones un pequeño brote se convierte en epidemia? Esta parece ser la pregunta fundamental que Watts intenta contestar aquí, y recurre, en principio, a la teoría epidemiológica clásica conocida como modelo SIR (Susceptibles, Infected, Removed o Recovered) para situar su procedimiento explicativo. Este modelo, planteado en sus inicios por los matemáticos William Kermack y A.G. McKendrick, prescribe la trayectoria incremental de una enfermedad de un modo estándar. Los contactos se presumen al azar y en las etapas iniciales la población contagiada es pequeña y la tasa de crecimiento es muy lenta (slow-growth phase). Sin embargo, si la densidad de infectados prospera hasta sobrepasar cierto umbral crítico, se inicia la fase de crecimiento explosivo en la que la tasa de infecciosidad alcanza su máxima virulencia (explosive phase). Luego de sobrepasado este momento la tasa de infecciosidad decrece hasta desaparecer ya que se hace sumamente difícil encontrar más víctimas, y aquí nos encontramos con la fase de extinción (burnout phase). Desde esta perspectiva el brote de Ebola no fue una epidemia porque no fue posible alcanzar una fase de crecimiento expansivo: la elevada letalidad del virus hizo que se pase del brote a la extinción directa. En definitiva, no se cumplió la condición de base para la formación de una curva de contagio ascendente, que es que en un momento dado se infecte más gente que la que es removida del circuito de infecciones.
En contraposición a este modelo regido por contactos al azar, Watts se plantea cómo actúa una epidemia en una red de mundo pequeño. En primera instancia si el contagio no es al azar y está confinado por las fronteras geográficas simples la infecciosidad decrece dramáticamente, ya que no cualquier ejemplar de la población puede contactar a cualquier otro. A pesar de esto los atajos propios de las redes de mundo pequeño introducen cuotas de aleatoriedad que los epidemiólogos necesitan tener en cuenta si desean frenar unos procesos epidémicos. Es decir, se debe actuar considerando la tipología de la red y no solo los dispositivos de contagio.
En general, y si se comparan las curvas de infecciosidad del contagio epidémico en redes de pequeño mundo y en redes regidas por el modelo SIR, se aprecia que en las redes de mundo pequeño la fracción de infectados crece continuamente en un gradiente desde 0 y no hay ningún proceso de explosión epidémica.
Posteriormente se vincula esta dinámica con los llamados «Modelos de Percolación«, teoría desarrollada originalmente a fines del siglo XIX en Alemania para estudiar los procesos de filtrado de una sustancia en un medio poroso, pero rehabilitada y extendida durante la segunda Guerra Mundial por Paul Flory y Walter Stockmayer.
Más allá de este interesante modelo, cuya aplicación demanda simplificaciones analíticas que Watts reconoce como poco realistas, el autor termina enfatizando una característica importante que tienen las redes de “pequeño mundo” estudiadas por Barábási y Albert: son más resistentes a los ataques al azar porque la conectividad no está distribuida de modo aleatorio. Es decir que, teniendo a Internet en mente, es poco probable pensar que procedimientos de ataque que no seleccionen nodos con mucha conectividad tengan un éxito importante. Como contrapartida, cualquier ataque que funcione con una lógica selectiva se vuelve altamente peligroso, lo cual sería inocuo en una red vinculada estrictamente al azar.
Tenemos que decir que la alternancia de temas y el pasaje de una cuestión pone realmente a prueba la noción de trabajo interdisciplinario defendida por el autor, ya que también su modelo se extiende a la comprensión de las burbujas financieras. ¿Cuales son los factores que producen estos procesos? ¿Qué puede decir la teoría de las redes de pequeño mundo de ellos? En primer lugar las teorías de la racionalidad económica suponen la existencia de un individuo cuasi-omnisciente que no parece ajustarse a los comportamientos reales. Las decisiones de las personas parecen basarse, sobre todo en ciertos períodos históricos, mucho más en la imitación o en la consideración de lo que los vecinos hacen que en la evaluación más o menos objetiva de las consecuencias de una conducta determinada. Fenómenos como la caída del muro de Berlín, por ejemplo, pueden atribuirse enteramente a este comportamiento masificado que los economistas denominan «cascada informativa» (information cascade). Sin embargo, a mayor o menor ritmo, las cascadas informativas ocurren permanentemente y no conciernen sólo a los momentos de modificación radical de comportamientos o conductas.
Considerando los antecedentes de los trabajos del psicólogo Solomon Asch y de Simon, quienes en la década del 50 investigaron la relevancia de lo que llamaron «externalidades» en la toma de decisiones, Watts reivindica en términos teóricos la capacidad explicativa de la denominada teoría de la «racionalidad con límites» en la explicación de las cascadas informativas.
En general, y cuando la gente no tiene suficiente información sobre un fenómeno, confía en la decisión de sus vecinos, y hasta es posible que actúe como ellos aún en contra de sus propias percepciones sobre la conveniencia de asumir o no determinada conducta. En rigor de verdad, lo que los economistas llaman «externalidades» no son elementos extraordinarios de la toma de decisiones colectivas e individuales sino sus componentes permanentes e imprescindibles.
Consideramos que hemos expuesto lo suficiente con vistas a que entendáis, el porque de los ataques a los productos Microsoft o como los mensajes que nos conminan a reenviarlo a más de seis o siete amigos son menos inocuos de lo que aparentan a la hora de difundir una idea, mensaje o virus informáticos. Internet está sujeto a muchas amenazas, algunas de las cuales distan de ser triviales aunque sean un tanto jocosas. Lean sino ustedes la siguiente noticia que apareció hace algunos meses en el rotativo El País: “El Ciberespacio es Submarino”.
Lo sorprende, una vez más, es que los mismos patrones son observados en los análisis de biodiversidad y edafodiversidad, de los que hemos hablado en tropecientas ocasiones en los post incluidos en la categoría: “Diversidad, Complejidad y Fractales”. Resulta obvio que topamos con leyes universales. No deja asaltarme el posible paralelismo entre este número seis y el siete que concierne a la Regla de Miller. De hecho, a veces en este último caso se tiene en cuenta el primer paso, es decir la persona que comienza la “cadena de favores” (¿recuerdan la película? Así, navegando en búsqueda de páginas que hablaran de mundos pequeños (small worlds), tope con una de las figuras de arriba que muestra una jerarquía de seis pasos (o siete, según se mire), justamente la de la estructura de la USDA Soil Taxonomy (taxonomía americana de suelos). Sin embargo. vean también la curiosa forma de describir el contenido de un libro en la última figura de este post. Fue analizando la mencionada clasificación yanqui como descubrí que se trataba de una estructura multifractal, conforme también al numero mágico de Miller (texto íntegro publicado en la revista de pago Geoderma el año 2006). Ya os comentamos también que la configuración subyacente a los diccionarios sigue los mismos patrones.
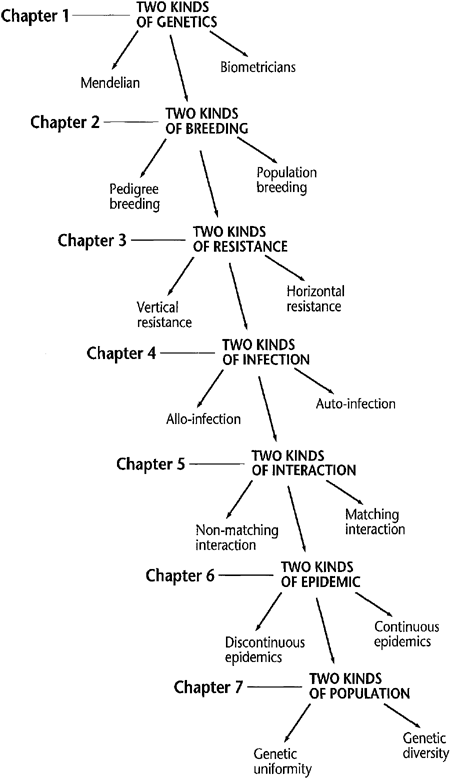
Jerarquía-estructura de un libro al buscar por “small worlds”
Fuente: Google images.
En términos ecológicos los sitios hiperconectados corresponderían a las especies clave de un ecosistema, como ya hemos visto en otro post que precede a este (ver abajo).
Información adicional ya ha sido escrita en los post incluidos en la categoría “Diversidad, Complejidad y Fractales
Post Previos Relacionados con el Tema
Redes y Sistemas Jerárquicos: Aspectos Funcionales
Concepto de Red y Sistema Jerárquico: Aspectos Estructurales
Redes Complejas: Redes Sociales y Redes Ecológicas (Los Mundos Pequeños)
Conectividad, Redes Sociales y Redes Ecológicas
Especies Clave y Nodos Clave: Redes Ecológicas, Redes Sociales
Evolución de la Biodiversidad a lo largo de la Historia de la Tierra
Evolución de las Redes Ecológicas y Cadenas Tróficas desde el Cámbrico hasta la Actualidad
Continuará…………
Juan José Ibáñez

[…] Transmisión de la información, Conectividad y Redes Sociales: El Número Mágico 6 o ¿7? […]