| |||||||||||||||||
 |
|
La premisa fundamental en la que se ha apoyado la Ciencia desde que Newton escribiera sus famosos "Principios Matemáticos de Filosofía Natural", a finales del siglo XVII, consiste en que la naturaleza posee unas determinadas leyes, que podemos representar en forma de ecuaciones algebraicas. A partir de ahí, tan sólo es necesario tener habilidad matemática. Si los resultados de las observaciones se ajustan a la descripción matemática, la ley es válida y, si de la fórmula utilizada, se realiza alguna predicción comprobable experimentalmente, tanto mejor. Las expresiones matemáticas que se utilizan en Física son todas ecuaciones diferenciales, en las que aparecen tanto una magnitud como sus derivadas. Una de las hipótesis de trabajo que se maneja es que, dado un sistema dinámico -un problema físico bien definido-, la solución de las ecuaciones que lo describen es única cuando se conocen con precisión las condiciones iniciales de las que se parte: si sabemos la posición de una bola en una mesa de billar -que supondremos exenta de rozamiento, para simplificar-, y la fuerza con la que la lanzamos, podemos deducir, con nuestras ecuaciones, su posición final en cualquier lapso temporal. Las ecuaciones son determinadas, y el mecanismo funciona como un reloj. Según este modelo, el Universo es, por lo tanto, mecánico y determinista. Esta forma de pensamiento se resume muy bien en un célebre aforismo de Pierre Simon de Laplace, uno de los científicos más destacados del siglo XVIII: "Un ser que conociera todas las fuerzas de la naturaleza y las posiciones de los seres que la forman, y que pudiera analizar estos datos, podría condensar en una sola fórmula el movimiento de los objetos más grandes del universo y el de los átomos más ligeros: nada sería incierto para dicho ser; tanto el futuro como el pasado estarían presentes ante sus ojos".
|
||||
| ¿Qué es la teoría del caos? |
|
Una definición de diccionario podría ser la siguiente: es el estudio del comportamiento inestable y no periódico de las soluciones de los sistemas dinámicos no lineales y deterministas. Esta definición debería satisfacer a muchos matemáticos y científicos, pero probablemente no signifique nada para un lector no especializado. El mejor modo de explicar qué es el caos es remontarnos un poco de su historia. Hacia 1960, un meteorólogo estadounidense llamado Edward Lorenz se encontraba analizando, por medio de un ordenador de válvulas de los de aquella época, cuál era el comportamiento de un modelo matemático que creía podría servir para representar el comportamiento de la atmósfera. El sistema que empleaba era muy complejo: una serie de ecuaciones diferenciales acopladas entre sí. En uno de sus cálculos, introdujo en la computadora los valores de un cálculo anterior, con el fin de comprobar, de manera rutinaria, que el cálculo era correcto, y se fue a tomar un té. Cuando volvió, observó que el comportamiento era totalmente diferente del que había hallado anteriormente, y encontró el por qué: para ahorrar papel, se imprimían únicamente los resultados con tres cifras decimales, en lugar de las seis que utilizaba la memoria del ordenador. Las diferencias se observaban al introducir en el ordenador tres cifras decimales en lugar de seis para las condiciones iniciales. Investigando acerca de este fenómeno, hizo una gráfica con el resultado de realizar 3000 iteraciones con las mismas ecuaciones, variando las condiciones iniciales en la cuarta cifra decimal. Ambas soluciones se comportaban de forma muy parecida durante las primeras 1500 iteraciones pero, a partir de ahí, divergían de forma drástica. Es decir, su sistema climático era especialmente sensible a las condiciones iniciales, de forma que cualquier alteración en un pequeño parámetro ocasionaba una evolución drásticamente distinta. Y de una forma un tanto metafórica, enunció el ya famoso "efecto mariposa": el clima es, en esencia, impredecible porque el débil aleteo de una mariposa en un punto del globo puede, a la larga, impedir que se forme una tormenta en la otra punta del globo, o bien ocasionar un huracán donde no debería tener lugar.    Conviene señalar que el artículo, aparecido en una revista especializada de meteorología, pasó desapercibido tanto a los meteorólogos - pues se trataba de un trabajo puramente matemático- como a los matemáticos -quienes no tenían ninguna razón para leer una revista de una disciplina bien alejada del interés matemático. Diagrama de Feigenbaum, que corresponde a la gráfica de la aplicación x -> kx (1-x) cuando x está entre 0 y 1, y k entre 0 y 4. El sistema conduce rápidamente al caos, y la imagen es un fractal con un factor de escala que ha resultado ser un número trascendente -al igual que pi o el número e, base de los logaritmos naturales. Este número es, aproximadamente, 4.6692. Un gran número de sistemas físicos responden a este preciso modelo.
|
|||||
| ¿Es la naturaleza caótica? |
|
Una vez establecido que el caos es un resultado matemático, cabe preguntarse hasta qué punto este resultado se puede encontrar en el mundo físico, es decir, si la naturaleza posee comportamiento caótico. Las ecuaciones que dan lugar al caos son las que representan a los sistemas dinámicos no lineales, como por ejemplo, las turbulencias en un fluido, las atracciones gravitatorias entre tres cuerpos, los péndulos sometidos a una fuerza externa, la población de las especies de un ecosistema que compiten entre sí, y otros muchos sistemas físicos. Cabe entonces preguntarse por qué no se ha detectado antes este tipo de comportamiento. Sencillamente, porque la mayor parte de los sistemas de ecuaciones que describen los sistemas dinámicos reales son tan complejos que encontrar una solución analítica resulta un auténtico milagro; la mayor parte de las veces se utilizan métodos aproximados para buscar las soluciones. Casi todos consisten en linealizar las ecuaciones: desarrollar en serie los términos que aparecen, comprobar la magnitud de cada uno de ellos, quedarnos con los de mayor peso y despreciar olímpicamente todos los términos de menor orden o, a lo sumo, tratarlos como una pequeña perturbación de los resultados que se obtienen, es decir, precisamente el punto de vista de que "causas parecidas ocasionan efectos similares". Nada se puede reprochar a este modo de proceder, pues mejor es obtener una solución aproximada a un problema real que no tener nada en absoluto. La otra forma que hay de obtener la solución a estos problemas es hacer análisis numérico, es decir, utilizar calculadoras y ordenadores que realicen un proceso de iteración hasta encontrar las soluciones. Estas herramientas, obvio decirlo, no aparecieron hasta la mitad del siglo XX.; y cuando se pusieron a calcular, nos mostraron que todos los términos que se despreciaban eran los que daban lugar al comportamiento caótico. La naturaleza es esencialmente no lineal. En el ejemplo anterior de la mesa con la bola de billar, un planteamiento correcto del problema debería tener en cuenta el rozamiento del tapete, las irregularidades de las bandas de la mesa, e incluso las irregularidades a escala atómica de la superficie del taco y de la bola. Si se incluyen estos efectos en nuestras ecuaciones, el billar resulta ser un ejemplo perfecto de comportamiento caótico. Afortunadamente - por lo menos para los jugadores de billar-, el rozamiento con el tapete frena el movimiento de la bola antes de que se manifieste este comportamiento, por poner una cifra al albur, a partir del segundo centenar de colisiones con la banda. |
||
| Los fractales |
|
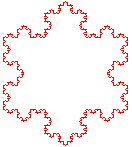
La gráfica que representa la solución del sistema de Lorentz, el conocido como atractor de Lorentz, es espectacular: un punto que oscila entre dos valores, de forma no periódica, a veces da dos vueltas sobre uno de los valores y cambia al otro, donde oscila una sola vez y vuelve hacia el primero. Estos atractores son característicos de un tipo de objetos matemáticos que poseen dimensiones fraccionarias, llamados fractales. Los fractales, conocidos sobre todo por lo espectacular de sus representaciones gráficas, son objetos que presentan la característica de la autosimilitud de escala, es decir, que al ampliar una pequeña zona del dibujo completo se obtiene una imagen que coincide, en esencia -a veces de forma idéntica-, con el dibujo original. Dibujar un fractal no es complicado; por ejemplo, si se divide un triángulo por medio de tres líneas que partan de los puntos medios de sus lados, y se repite la operación con los triángulos que se forman, se obtiene un fractal sencillo, conocido como el triángulo de Sierpinski. Uno de los más conocidos es el copo de nieve de Koch: se dibuja un triángulo equilátero; a continuación se dibuja, en cada uno de los lados, y en su tercio medio, un triángulo equilátero de un tercio del tamaño, y se sigue indefinidamente. Este ejemplo ilustra muy bien qué es un objeto de dimensión fraccionaria. El copo de nieve de Koch, aunque es una figura plana, posee una longitud infinita; figuras semejantes a ésta fueron obtenidas por eminentes matemáticos, como George Cantor, Gaston Julia y Benôit Mandelbrot -quien acuñó el término de fractal-, precisamente utilizando iteraciones de funciones matemáticas, exactamente el mismo camino que siguió Lorentz con su modelo climático.
El modelo de Cantor es especialmente interesante: dibújese una línea recta, divídase en tres tramos iguales y quítese el tercio del medio; procédase del mismo modo con los dos tramos restantes. Si seguimos realizando esta división obtendremos una figura muy curiosa: un conjunto infinito de puntos cuya longitud total es cero. Curiosamente, este modelo se ha aplicado con éxito para explicar los fallos en la transmisión de señales de telecomunicaciones: en medio de una comunicación parece haber un corte que, al ser examinado con más detalle, se corresponde con varios tramos de transmisión correcta alternados con otros cortes, y así sucesivamente. Otros muchos fractales se han empleado para describir figuras naturales: la superficie de las nubes, la línea de la costa, la superficie de los virus, las hojas de los helechos o las conexiones sinápticas de las neuronas del cerebro.
Hasta ahora, el conocimiento que se tenía de la naturaleza era, en gran medida, esencialmente cualitativo y, en contados casos, cuantitativo, habida cuenta que únicamente se pueden resolver de manera analítica un reducido número de expresiones matemáticas. La nueva matemática asociada al caos nos está permitiendo ahondar en el estudio de los sistemas complejos, en condiciones que se encuentran lejos del equilibrio, es decir, de un modo mucho más acorde con la realidad de la naturaleza que los modelos matemáticos estudiados hasta ahora. Es una teoría que aún tardará bastante en desarrollarse por completo, pero intervendrá decisivamente en todos los campos de la Física, la Biología, la Meteorología, la Ingeniería y la Informática. Para saber más Para saber menos
|
|||||||||