Los inicios de la computación: la máquina de Turing

Queda ya menos de un mes para que se celebre en Madrid el Simposio Internacional de Alan Turing organizado por la Real Academia de Ciencias. El congreso traerá a la Fundación Areces a expertos mundiales en las ramas de la ciencia de las que fue precursor el matemático inglés. Inteligencia Artificial, computación, lógica, criptografía, matemáticas aplicadas a la biología… aun hoy, casi sesenta años después de su muerte, todos estos campos siguen estando tremendamente influidos por el trabajo visionario de Turing.

Durante estas semanas estamos haciendo una breve introducción de algunos de estos temas y de su representación en el congreso, destacando los ponentes que transmitirán la importancia del legado de Turing en sus respectivos campos. Seguimos con su impacto más reconocido –por algo le llaman el padre de la computación moderna.

El trabajo de Alan Turing es considerado precursor de toda la computación moderna que hoy determina nuestra sociedad, nuestras maneras de producir, las relaciones, los medios de transporte, el avances del conocimiento, e incluso nuestra manera de pensar. Sus desarrollos en la formalización de los conceptos de algoritmo y computación mediante la llamada máquina de Turing fueron fundamentales para el avance de las tecnologías de la información.

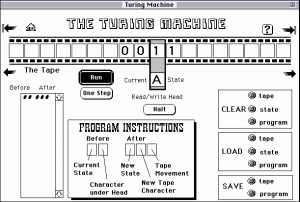
Una máquina de Turing es un dispositivo que manipula símbolos sobre una tira de cinta de acuerdo a una tabla de reglas. A pesar de su simplicidad, puede ser adaptada para simular la lógica de cualquier algoritmo de computador y es particularmente útil en la explicación de las funciones de un CPU dentro de un ordenador.

En realidad, no está diseñada como una tecnología de computación práctica, sino como un dispositivo hipotético que representa una máquina de computación, pero sus componentes (la cinta, el cabezal, el movimiento, la lectura) podrían ser implementados.

Sobre los números computables

La máquina fue descrita por Turing como una máquina automática en 1936 en la revista Proceedings of the London Mathematical Society, en el estudio «Sobre los números computables, con una aplicación al Entscheidungsproblem».

En este artículo se estudiaba la cuestión planteada por David Hilbert sobre si las matemáticas son decidibles, es decir, si hay un método definido que pueda aplicarse a cualquier sentencia matemática y que nos diga si esa sentencia es cierta o no, el llamado Entscheidungsproblem. Turing ideó un modelo formal de computador y demostró que existían problemas que una máquina no podía resolver, y que determina los límites de la ciencia (profundizaremos sobre este tema en una futura entrada).

La idea básica de todo el formalismo de Turing es que reduce el concepto de ‘método’ a operaciones simples que pueden, de manera incuestionable, ser efectuadas. Estas operaciones sencillas son la serie de instrucciones lógicas en las que se basan las acciones del artilugio. En esta idea radican las bases del concepto moderno de algoritmo.

Con su máquina, Turing describió en términos matemáticos precisos cómo un sistema automático con reglas extremadamente simples podía efectuar toda clase de operaciones matemáticas expresadas en un lenguaje formal determinado.

Definición de Turing

Turing definía su creación como:

“  …una ilimitada capacidad de memoria obtenida en forma de una cinta infinita marcada con cuadrados, en cada uno de los cuales podría imprimirse un símbolo.

En todo momento hay un símbolo en la máquina, llamado el ‘símbolo leído’, que la máquina puede alterar. El comportamiento de la maquina está en parte determinado por el símbolo leído, pero no por los símbolos en otros lugares de la cinta.

Una de las operaciones elementales de la máquina es el movimiento hacia adelante y hacia atrás a través de la máquina de la cinta, por lo que cualquier símbolo en la cinta puede convertirse en el símbolo leído. (Turing 1948, p. 61)”

La máquina de Turing modela matemáticamente un dispositivo que opera mecánicamente sobre una cinta. En esta cinta hay símbolos que la máquina puede leer y escribir, uno a la vez, usando un cabezal lector/escritor de cinta.

La operación está completamente determinada por un conjunto finito de instrucciones elementales como «en el estado 42, si el símbolo visto es 0, escribe un 1; Si el símbolo visto es 1, cambia al estado 17; en el estado 17, si el símbolo visto es 0, escribe un 1 y cambia al estado 6; etc.».

Esto se repite según se indique en la función de transición, para finalmente detenerse en un estado final o de aceptación, si la cuestión planteada es ‘computable’, es decir, realizable por la máquina de Turing actuando sola.

En el simposio:

“La lógica, la computación, la representación del conocimiento y la resolución de problemas”, David Pearce (Universidad Politécnica de Madrid). Miércoles 24 de octubre, 12:30. Salón de actos de la Fundación Areces.

El Simposio Internacional: ‘El legado de Alan Turing’, organizado por la Real Academia de Ciencias Exactas, Físicas y Naturales, tendrá lugar el 23 y 24 de octubre en la Fundación Areces. El encuentro reunirá a importantes investigadores en los campos de los que fue precursor el matemático Alan Turing. Entre los ponentes hay primeras figuras en campos como la inteligencia artificial, la lógica, la computación, la criptografía, y otros temas. El programa completo puede consultarse en la página de la Fundación Areces.

Recordamos que todavía está abierto el periodo de subscripción (gratuita) para el Simposio. Se puede rellenar el formulario de inscripción en la página web de la Fundación Areces.

—

Ágata A. Timón es responsable de Comunicación y Divulgación del ICMAT.