Y para continuar, hablemos de complejidad

Este es un blog de redes complejas por lo que se hace necesario comentar lo que entendemos por complejidad y su relación con las redes complejas.

Hasta hace relativamente poco, unos 30 años, el pensamiento científico dominante era el reduccionismo, cuyo enfoque considera que basta un conocimiento detallado de cada uno de los componentes de un sistema y de sus leyes fundamentales para entenderlo globalmente (1,2,3). El truco está en que esto sólo es posible si el sistema es lineal, de tal forma que se puede descomponer en cada una de sus partes, cuyo comportamiento dinámico es conocido, analizarlas de forma independiente y volverlas a juntar para entender cómo  se comporta el conjunto, como un cristal de sal o el aire que respiramos. A pesar de que todos ellos están formados por una cantidad ingente de partículas son sistemas tratables desde el punto de vista físico porque, en promedio, todas sus partículas se comportan igual. Pero la mayoría de los sistemas son no lineales (sistemas con umbral que amplifican pequeñas perturbaciones). Por ejemplo nuestro sistema auditivo, cuando escuchamos nuestra canción favorita no obtendremos el doble de placer si la escuchamos al mismo tiempo de dos fuentes diferentes,  o no importa cuánto sepamos de la dinámica de una neurona para poder entender el comportamiento del cerebro como la memoria o el lenguaje. Es debido a esta imposibilidad de reducir algunos sistemas como la suma de sus componentes, que conviene diferenciar entre sistemas complicados y sistemas complejos.

Para entender mejor la diferencia entre los distintos tipos de sistemas es ilustrativa la siguiente figura donde se representan estos dos extremos en función del número de grados de libertad  (variables que describen el sistema) y el grado de no linealidad presente en el sistema. En la parte izquierda del diagrama «viven» los sistemas simples, aquellos sistemas formados por pocos elementos y cuyo comportamiento dinámico, simple o no (periódico, caótico,…),  se conoce perfectamente.

Un sistema complicado (esquina inferior derecha) es el resultado de conectar, un gran número de elementos con comportamiento lineal, es decir, cuyo comportamiento está acotado y es el esperado bajo el efecto de pequeños cambios externos (todas las máquinas creadas por el hombre). Por el contrario, un sistema complejo  (esquina superior derecha del diagrama) es el resultado de la interacción de muchos elementos donde existe un cierto grado de no linealidad, bien en los elementos que componen el sistema o en la misma interacción o en ambas a la vez. De los sistemas complejos se pueden esperar comportamientos críticos. Es precisamente en la frontera entre el orden (un cristal) y el desorden (un gas) donde surge la complejidad, la emergencia de un comportamiento nuevo colectivo cualitativamente diferente de las propiedades de los componentes elementales del sistema. Por ejemplo, una neurona (o una célula del corazón, esquina superior izquierda) cuando recibe un estímulo por encima de un umbral puede responder de forma periódica o caótica. Sin embargo, si conectamos unas pocas neuronas, el resultado puede llegar a ser una actividad eléctrica síncrona debido a la interacción sináptica entre ellas. Esta sincronización de la actividad eléctrica en los circuitos neuronales que surge por el simple hecho de conectar unas pocas neuronas, se cree que es el mecanismo mediante  el cual el cerebro procesa y codifica la información. Si tenemos en cuenta todo el sistema nervioso, cerebro, médula y el sistema nervioso periferico, estamos ante el más complejo de los sistemas conocido en el universo.

Además del factor de la no linealidad y del gran número de elementos, otra capa de complejidad a añadir es la estructura en que los distintos elementos interaccionan.

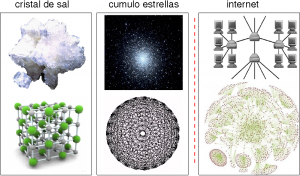
Por ejemplo, en la sal común (izquierda),  la naturaleza de la estructura del cristal nos ayuda a simplificar el problema asumiento que cada átomo sólo interacciona con sus átomos vecinos dando lugar a una estructura de red de malla, estructura ordenada. En un cúmulo de estrellas (centro), cada una de las estrellas interacciona con el resto, lo que también permite una simplicación matemática muy grande.

Este tipo de conectividad es el que podemos encontrar en las aproximaciones clásicas reduccionistas aplicadas a sistemas complicados. Sin embargo, muchos sistemas reales, complejos, muestran un patrón diferente de conectividad que no permiten tales simplificaciones. Por ejemplo, la red de conexiones físicas entre ordenadores (derecha), Internet, presenta una estructura más compleja que las anteriores pues el número de ordenadores a los que un ordenador cualquiera de la red está conectado no es uniforme.

Es aquí, precisamente, donde entra en juego la teoría de redes complejas, una herramienta que permite la representación del conjunto de interacciones en un sistema complejo por medio de un grafo, donde cada elemento del sistema es representado por un nodo (ordenador) y la interacción entre dos de sus elementos se corresponde con el enlace (cable de red). Gráficamente, los nodos se representan mediante puntos y los enlaces como segmentos entre esos dos puntos. Dada la simplicidad de esta metodología, las redes aparecen en todas partes (4), sobre todo en biología. Por ejemplo, el genoma, el conjunto de genes de un organismo, difiere muy poco de un organismo a otro (menos del 1% entre el genoma humano y el del resto de los primates) y se puede analizar a través de la red de las relaciones entre genes cuya expresión es regulada mediante la activación y la desactivación entre ellos. Con lo cual, cabe esperar que la red de regulación genética en el ser humano es sea mucho más compleja (medida según parámetros topológicos de teoría de grafos) que en el resto de un primates.  No hay genes «buenos» o «malos», lo que nos hace diferentes está en la complejidad de la red.

(1) P. W. Anderson, More is different, Science 177, 393–396 (1972)

(2)  P. Bak, How Nature works, Oxford Univ. Press (1997)

(3) S. Solomon y E. Shir, Complexity; a science at 30, Europhysics News 34 (2003)

(4) D. J. Watts, Small worlds: The dynamics of networks between order and randomness, Princeton University Press, Princeton, New Jersey (1999)