![]()
Nanomateriales (3): la fibra ideal
Manuel Elices Calafat (Universidad Politécnica de Madrid; Real Academia de Ciencias Exactas, Físicas y Naturales; National Academy of Engineering USA)
Nanotubos de carbono
En 1991 Sumio Iijima (Iijima S. (1991) Helical microtubules of graphitic carbon. Nature 354, 56-58), trabajando en un laboratorio de investigación básica en Tsukuba, Japón, descubrió una aguja en un pajar que ha revolucionado la nanociencia. La aguja era un cilindro hueco que se había formado en la punta de un electrodo de grafito. Tenía un diámetro de unos pocos nanómetros y una longitud de unas cuantas micras. Estaba hecha de carbono puro. Era un nanotubo de carbono.
Desde su descubrimiento hasta nuestros días, las aplicaciones de los nanotubos —algunas reales, otras potenciales— han crecido de forma impresionante. Es posible que los nanotubos de carbono desempeñen el mismo papel que el silicio en los circuitos electrónicos, pero a escala molecular, donde el silicio y otros semiconductores dejan de funcionar. Ya se han fabricado con nanotubos dispositivos lógicos —los componentes básicos de los ordenadores— y se han creado expectativas para producir, a partir de ellos, circuitos electrónicos e incluso ordenadores. Los nanotubos de carbono han permitido mejorar la resolución de los microscopios de barrido basados en el efecto túnel, se han usado como sondas químicas en microscopios de fuerza atómica y como sensores extremadamente sensibles.
En el incio del siglo XXI, unos investigadores japoneses (Gao Y., Bando Y. (2002) Carbon nanothermometer containing gallium. Nature 415, 599) fabricaron el termómetro más pequeño del mundo llenando con galio un nanotubo de carbono. La altura de la columna de galio en el nanotermómetro varía linealmente con la temperatura, mientras que el diámetro del nanotubo apenas varía, debido al pequeño coeficiente de dilatación del tubo. El nanotermómetro opera entre 50 y 500˚C y puede resultar muy útil para medir la temperatura en una gran variedad de microambientes. Sólo tiene un pequeño inconveniente: hace falta un microscopio electrónico para leer la temperatura del termómetro.
La estructura de los nanotubos de carbono se ha observado utilizando microscopía electrónica de transmisión de alta resolución. La forma ideal de un nanotubo se puede obtener enrollando una lámina de grafito, como la indicada en la figura anterior, haciendo coincidir el extremo A del vector OA(n, m) con su origen O de manera que OA sea la circunferencia directriz del cilindro. Las estructuras más simétricas se obtienen a partir de los vectores (n, 0) —llamadas en zig-zag, donde q = 0˚— y de los vectores (n,n) —llamadas en butaca (armchair), donde q = 30˚—. Las estructuras intermedias, donde 0 < q < 30, se llaman quirales porque pueden existir en dos formas con simetría especular. Los extremos de los tubos de carbono se cierran con medias moléculas de fullereno. Las estructuras que se observan frecuentemente son tubos de varias paredes, formadas por la superposición de tubos coaxiales. Son estructuras que recuerdan a las muñecas rusas.
La fibra ideal
Cuando los átomos de carbono se unen para construir un diamante lo hacen mediante cuatro enlaces covalentes y forman una rígida red tridimensional que le confiere a la preciada gema su proverbial dureza. Cuando se unen para construir grafito, los átomos de carbono lo hacen a través de tres enlaces covalentes situados en un plano; la estructura sigue siendo muy resistente en este plano pero es débil en dirección perpendicular. Una forma de aprovechar esta resistencia es orientar estos planos de forma que las direcciones de máximo esfuerzo estén contenidas en ellos.
Basta imaginar un mil hojas y tirar en la dirección paralela a las hojas en vez de hacerlo en dirección perpendicular. Arrollando estas hojas, como si fueran las de un cigarro puro, se pueden obtener fibras de carbono muy resistentes.
Ya se producen, desde hace algún tiempo, fibras de carbono con esta estructura y se utilizan (embebidas en una matriz polimérica) para fabricar palos de golf, cañas de pescar, coches de fórmula uno y aviones de combate. Estas fibras son rígidas (tienen un módulo de elasticidad elevado) y resistentes (una tensión de rotura grande) pero sus valores todavía están lejos de los valores teóricos debido a sus defectos e imperfecciones. Cuando se descubrieron los nanotubos de carbono —con una estructura casi perfecta— se despertaron muchas esperanzas y se empezó a especular sobre la posibilidad de obtener fibras ideales.
Muy pronto se hicieron estimaciones teóricas de las propiedades mecánicas de los nanotubos (Overney G., Zhong W., Tomanek D. (1993) Structural rigidity and low frequency vibrational modes of long carbon tubules. Zeit. Physik D 27, 93-96) y se confirmó que deberían poseer una rigidez y una resistencia superiores a cualquier otra fibra conocida, (módulo de elasticidad E = 1250 GPa y tensión de rotura, sR, alrededor de 60 GPa), pero la comprobación experimental de estas predicciones no resultó fácil por la pequeñez de los nanotubos y la dificultad de su manipulación; basta imaginar de qué forma se podría realizar un ensayo de tracción con una fibra de 5 nm de diámetro y 1 mm de longitud.
Por otra parte, R.S. Ruoff y sus colaboradores (Yu M.F., Files B.S., Arepalli S., Ruoff R.S. (2000) Tensile loading of ropes of single wall carbon nanotubes and their mechanical properties. Phys. Rev. Lett. 84(24), 5552-5555) se las ingeniaron para ensayar a tracción 15 nanotubos de una sola capa. En algunos observaron que la deformación en rotura llega a alcanzar valores del 5%. También medieron las fuerzas en el momento de la rotura, obteniendo valores entre 400 y 1300 nN. Suponiendo que esta carga está soportada uniformemente por el borde del nanotubo, dedujeron que las tensiones de rotura deberían oscilar entre 13 y 52 GPa. A partir de estos resultados también se puede estimar el módulo de elasticidad; el valor más alto —para una tensión de rotura de 52 GPa y una deformación del 0.05— es de 1040 GPa.
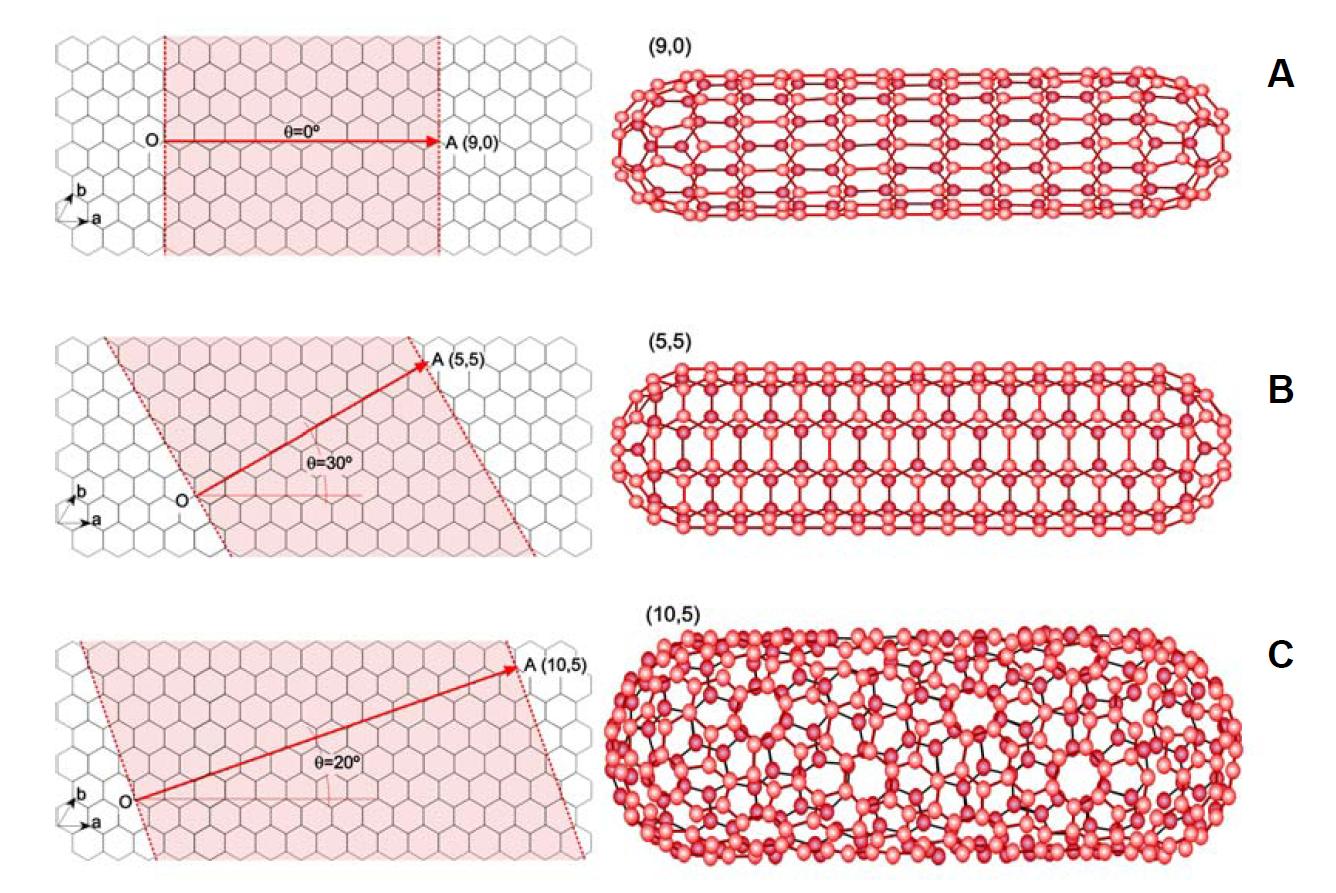
Estos resultados son muy parecidos a las predicciones teóricas, anteriormente señaladas, y están lejos de los mejores valores alcanzados por las fibras comerciales como el Kevlar® (E = 120 GPa, sR = 3 GPa), el acero (E = 210 GPa, sR = 3 GPa), o algunas fibras de carbono (E entre 250 y 800 GPa y sR entre 3 y 4 GPa) como se muestra en la figura siguiente.
La aparente sencillez del nanotubo de carbono ha estimulado cálculos teóricos más precisos y simulaciones utilizando dinámica molecular. J. Bernholc y sus colaboradores (Bernholc J. (1999) Computational materials science. Physics Today Sept., 30-35; Bernholc J. et al. (2002) Atomic transformations, strength, plasticity, and electron transport in strained carbon nanotubes. In Fiber Fracture (M. Elices, J. Llorca Eds.), Elsevier, Chap. 15) han simulado la respuesta de un nanotubo a un ensayo de tracción y han observado que pueden comportarse de forma dúctil o frágil, según las condiciones de contorno y la simetría de los nanotubos. A partir de un valor crítico de la tensión, el nanotubo libera parte de la energía elástica almacenada creando defectos (ver figura).
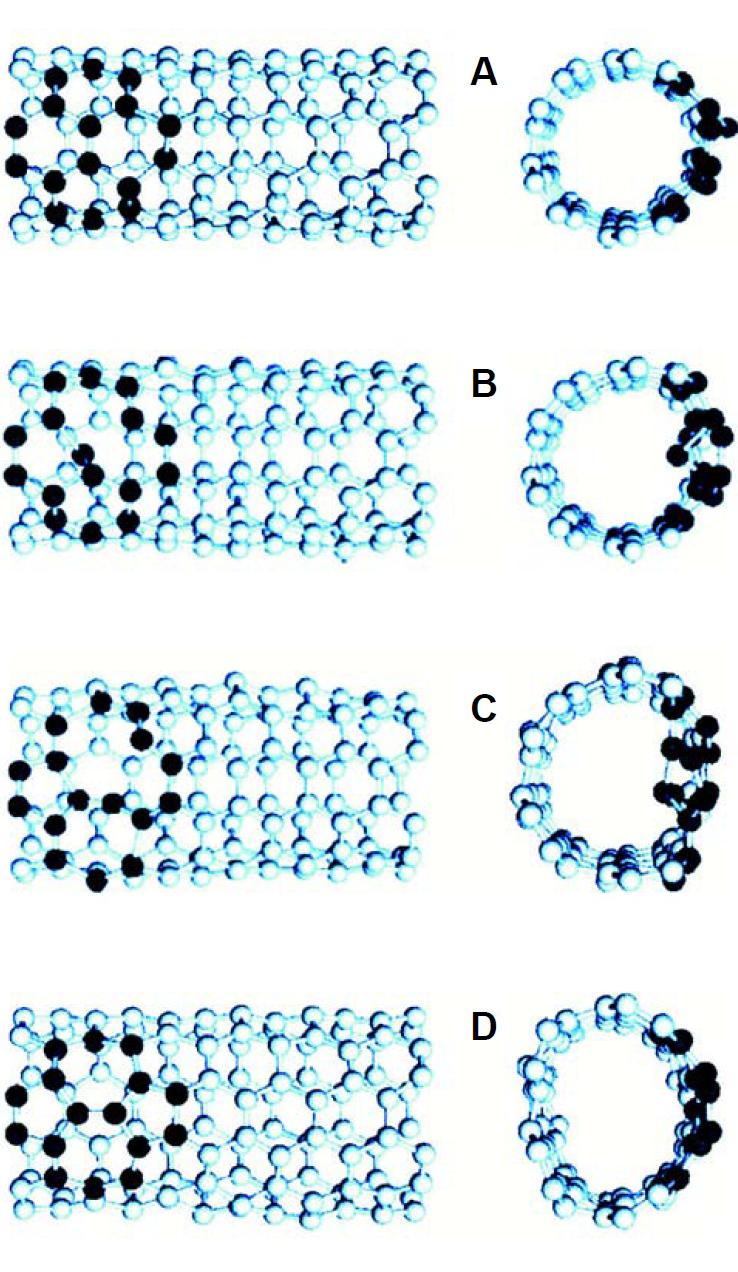
Los cálculos indican que esto sucede cuando la deformación es del orden del 5%. Estos defectos pueden disparar la rotura o bien formar dislocaciones que iniciarán una deformación plástica. Nuevamente, la deformación crítica del 5% indica que los nanotubos pueden soportar tensiones de 60 GPa.
A pesar de todo lo anterior, es en el campo de las propiedades electrónicas donde las predicciones teóricas ofrecen resultados más expectaculares como veremos en el post de la próxima semana.
