![]()
Las velocidades cuánticas de Boltzmann
La última revolución de la Física comenzó en 1870 cuando Ludwig Bolztmann empezó a intentar deducir la fórmula de Maxwell para la distribución estadística de las velocidades moleculares de un gas contenido en un recipiente cerrado y finito. En 1877 publicó el trabajo
Ludwig Boltzmann – Ueber die Beziehung zwischen dem zweiten Hauptsatze der mechanischen Waermetheorie und der Wahrscheinlichkeitsrechnung…}
Sitzungberichte der Kaiserlichen Akademie der Wissenschaften. Mathematisch‑Naturwissen Classe, Abt. II, LXXVI (1877) 373–435 (Wien)
en el que probaba la exactitud de las ideas de Maxwell.
Boltzmann había publicado ya la relación entre la demostración analítica del segundo Principio de la Termodinámica y el cálculo de probabilidades en 1871. En el trabajo de 1877 señala que la idea de tendencia al equilibrio en sistemas separados del mismo implica que el estado de equilibrio tiene una alta probabilidad de alcanzarse en el movimiento aleatorio de las moléculas del gas en el recipiente cerrado.
Pero es preciso establecer con un cierto rigor que se quiere decir al hablar de probabilidad de los estados de un gas, o la probabilidad de una cierta distribución de velocidades moleculares o equivalentemente de sus cuadrados, es decir, de su energía.
Si asumimos que las velocidades moleculares pueden tener cualquier valor en un continuo de números reales, no es posible realizar ningún cálculo de probabilidades, pues entre cada dos números reales hay una cantidad todo lo grande que se quiera de otros números reales. (Avanzando en el tiempo, el principio de incertidumbre de la Mecánica Atómica nos dice que la velocidad de cualquier molécula o átomo de un gas no es un número real concreto, sino que oscila constantemente en un cierto intervalo. Los intervalos son discretos).
Boltzmann introduce la noción de intervalos de velocidades o equivalentemente, de energías (Si las partículas del gas tienen todas la misma masa, podemos normalizar ésta a la unidad, y la energía de cada partícula será v², descartando la posición del recipiente en un campo de fuerzas derivado de un potencial).
Así, podemos partir el espacio de energías en intervalos finitos caracterizados por un único valor epsilon ε, dentro del cual la energía de la partícula puede ser [ ε-Δε, ε+Δε ] con Δε fijo y pequeño, y los valores reales de la energía dentro del intervalo carecen de importancia.
Esta es la hipótesis cuántica que refleja la realidad del mundo, enunciada por Boltzmann 23 años antes de que lo hiciese Planck.
Pero las ideas de Boltzmann se apreciaban poco en el ambiente científico alemán, y la idea pasó desapercibida, al menos hasta 1899.
Una vez que tenemos una colección de intervalos (0, ε, 2ε, …, nε, …) = (0,1,2,3,….,n…), normalizando a ε=1, con n ∈ N, donde N son los números naturales , la derivación de las probabilidades es larga pero directa y se llega a la fórmula de Maxwell:
f(v²) =K1(v²exp(v²))
e introduciendo la temperatura del gas en el recipiente, T, (temperatura proporcional a la energía media de las moléculas del gas):
f(v²,T, m=1) = KT(-3/2)v² exp{-v²/(2kBT)}, v²=nε, n ∈ N
donde he englobado en K todas las constantes que no cambian la forma de la distribución.
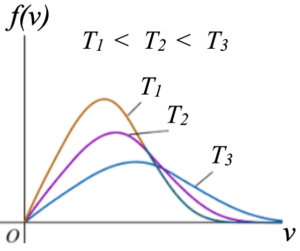
Esta distribución de velocidades de un gas de átomos o moléculas simples indica un número de moléculas igual a 0 para energías nulas, y un número de moléculas tendiendo a cero de forma exponencial cuando las energías son muy altas, dependiendo de la temperatura del gas la posición correspondiente al máximo número de moléculas con una cierta energía.
Es claro que la gráfica, como cualquier gráfica, es discontinua si la observamos con la amplificación suficiente, por ejemplo, en Photoshop o en Gimp.