Las sugerencias pseudo-cuánticas de Planck y Einstein

Durante todo el siglo XIX la forma del espectro de energías de la radiación del cuerpo negro mantuvo en vilo a los físicos de Alemania e Inglaterra. Un cuerpo negro es una cavidad con paredes ennegrecidas mediante polvo de carbón, que se mantiene a una temperatura dada T, y que solo tiene una pequeña abertura para dejar escapar la radiación electromagnética (EM) que se produce en su interior. La radiación está producida por los saltos de los electrones de los átomos de carbono de su superficie de unos niveles de energía a otros, pero en la época de Planck la idea de átomo era aún una entelequia, y Planck habla en sus trabajos de «resonadores», sin especificar qué puedan ser éstos, pero se deduce que los considera dipolos eléctricos capaces de absorber y emitir esa radiación EM.

En vez de partir de la emisión de radiación EM por átomos de carbono a temperaturas mayores del cero absoluto, supone que esa radiación ya ha sido emitida y llena la cavidad, el «cuerpo negro».  Para Planck, los resonadores absorben y re-emiten la radiación, hasta que se alcanza un equilibrio entre absorción y emisión, equilibrio que depende de la temperatura T.

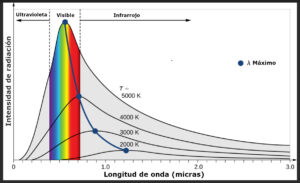
Evidentemente, en el equilibrio, la radiación EM contiene una cantidad enorme de frecuencias, según una curva del tipo de la figura adjunta, que se presenta en función de la longitud de onda que es la velocidad de la luz, c, dividida por la frecuencia ν: λ=c/ν.

Figura 1

Considera -un- único resonador con una frecuencia monocromática, ν, pero en la misma línea de su trabajo afirma que la amplitud A y la fase de esa radiación varían de manera aleatoria. No explica como la radiación del cuerpo negro tiene la dispersion de frecuencia ν.  Afirma que la energía U de cada resonador es la media en el tiempo de su energía real que fluctúa o, equivalentemente, el promedio de la energía  de un número muy grande de resonadores idénticos, cada uno con una energía individual U_i  diferente de la de los demás, y  U =<U_i>, con i perteneciente a un conjunto (1,2,…,M) de resonadores, donde < … > denota el operador promedio.

Así pues, salta de -un- único resonador a una situación real en el cuerpo negro: Un número muy grande de resonadores de frecuencia ν, dentro de otro número aún mucho mayor de resonadores con otras frecuencias, desde casi cero a las frecuencias de los rayos cósmicos. Pero no lo dice.

 Ahora,  la energía total U_M  del conjunto de resonadores con energía media U = <U_i>,  (proporcionada por algún elemento calefactor que mantenga el cuerpo negro a una temperatura T constante) es U_M=MU=M<U_i> , y su entropía  S_M=MS.  Deja en un limbo lo que pueda ser S, aunque la entropía S_M se debe a la aleatoriedad con la cual la energía U_M  se reparte entre los M resonadores. 

Puesto que Planck parte de las ideas expresadas en el artículo de 1877 de Boltzmann, Planck hace, como en el caso de las velocidades moleculares de Boltzmann, la substitución de las energías por intervalos de energía (U-ΔU, U+ΔU) = (U-ε,U+ε), donde ΔU = ε  y esos intervalos son discretos. Así, la energía total es U_M   y  U_M= Jε, donde J es un número natural.  Queremos obtener la entropía en función de U  y ε. 

Ahora Planck citando, aquí sí, a Boltzmann, asume que la entropía es igual a una constante k por el logaritmo de  la probabilidad P de que al mantener el cuerpo negro a una temperatura T  los M resonadores mantengan una  energía total U_M   y   S_M= k ln(P)+ cte.

Ahora, ¿cómo calcular la probabilidad? Siguiendo de forma estricta a Boltzmann, y usando sus mismos símbolos, Planck asume, como no puede asumir otra cosa, y como he señalado más arriba, que la energía   U_M(ε) = Jε, donde ε es una cierta cantidad fija, no variable, de energía, que se puede suponer pequeña respecto de U_M , y J un número natural grande J∈N.  Al hacer esta suposición, Planck está obligando a la energía total de un conjunto de resonadores iguales entre sí, con energía individual U_i a depender de un parámetro ε: U_M= U_M(ε). Si no se hace así, no se puede aplicar el concepto de probabilidad. Pero, la naturaleza ¿elige la distribución de energía en intervalos discretos? ¿O son esos intervalos discretos consecuencia de la estructura de la materia?  Planck no se preocupa de eso. 

La probabilidad es el número de formas posibles de repartir  la energía Jε  entre  M  resonadores. Es decir, las combinaciones con repetición de como repartir   J   energías  ε  entre   M resonadores. Usando, como Boltzmann, la combinatoria, y tras un razonamiento mucho más corto que el de éste,  obtiene la fórmula

es decir, la entropía de los M resonadores es una función exclusivamente de (<U_i>/ε), el cociente entre la energía media de M resonadores cuya energía   U_i  es variable en el intervalo (U-ε, U+ε)

Puesto que ya Wien había formulado que la entropía de un resonador, o más bien, de un conjunto de resonadores de la misma frecuencia, en un campo de radiación EM tenía que ser de la forma  S=f(U/ν), deduce Planck que la cantidad ε tiene que ser igual a una constante, cuyo símbolo elige como h, multiplicada por ν :

ε = hν

Para cada frecuencia ν, ε es fija pero diferente de unas frecuencias a otras. 

Puesto que por la Termodinámica sabemos que  1/T = dS_M/dU, derivando arriba podemos encontrar que 

1/T = [k/(hν)] ln (1+hν/U)

y de aquí

U(ν,T) = ε/(exp(ε/kT) – 1) = hν /(exp(hν/kT)-1)

que con los ajustes de las constantes necesarios coincide con la distribución de la energía con la frecuencia y la temperatura de la figura 1, y donde las frecuencias ν = ε/h son discretas como lo es ε.

Recordemos que ε es una cantidad fija, cuyo múltiplo entero Jε es la energía total de M resonadores de frecuencia ν.

Planck consigue encontrar la distribución buscada de la energía de la radiación EM introduciendo tres suposiciones: a) Que los resonadores individuales, y por tanto, la radiación que emiten tienen entropía, b) Que la energía (constante) de un único resonador es el valor medio en el tiempo de esa misma energía variable del mismo resonador, y es equivalente a la energía media de un número grande de resonadores exactamente iguales  y c) Que la energía total de un conjunto de M resonadores de frecuencia ν es Jε, donde J es un número natural. 

Recordemos que U es la energía media en el tiempo de un resonador, o el promedio de energías de M resonadores idénticos, que por hipótesis varían de resonador a resonador. ε no puede ser el mismo número para resonadores de frecuencias distintas, o bien existe un ε₀  del cual son múltiplos todos los ε.  Por lo tanto, si ε es una cantidad fija y no variable de energía,  las frecuencias ν del conjunto de resonadores del cuerpo negro tienen que ser discretas. 

De esta manera Planck debería haber sacado una conclusion clara:  Los componentes del cuerpo negro (hoy átomos de carbono) no emiten ni absorben radiación de frecuencia continua, sino discreta.  La radiación está cuantizada porque la materia es discreta, tanto como entidad física como en su capacidad de producción de energía.  De cualquier forma, y cómo veremos en otro post, la curva de radiación no exige, para su determinación, la hipótesis de cuanticidad. 

Einstein analiza la emisión de electrones de un cátodo cuando este recibe luz de alta o baja energía total siempre que la frecuencia de la luz supere un valor crítico dependiente del metal de que esta hecho el cátodo. Es claro que la frecuencia crítica depende de los átomos del metal, y no de la radiación. Si se denomina «cuanto de luz» a la cantidad hν, cuando la frecuencia es la correcta la incidencia de un cuanto de luz sobre un metal hace que un electron escape de la superficie del metal sin energía cinética.  Ahora, si iluminamos ese mismo metal con luz de frecuencia 2ν, se extrae el mismo electron pero con energía cinética hν.  En un metal cuya energía de extracción sea Φ, si hν es menor que Φ, el electron no sale, solo sale si hν es mayor que Φ. 

Los efectos son cuánticos, la radiación no lo es. 

Como veremos, la cuantización deriva de la ecuación de Shroedinger, no de los valores de ε, o equivalentemente, de hν.