Escher y la banda de Moebius. Antonio Córdoba.

Enlace a La banda de Moebius benedettina y a La botella de Klein de Antonio Córdoba Barba en poesía y ciencia

El pasado 30 de septiembre en La noche europea de los investigadores tuvo lugar en Espacio Fundación Telefónica la actividad titulada La alegría de las musas. Poesía y ciencia.

Pretendíamos realizar un encuentro entre poetas-científicos y el público para reflexionar y debatir sobre la conexión existente entre poesía y ciencia. Además, hubo un recital de poemas sobre ciencia escritos por científicos  y se entregó el premio del I Certamen de poesía y ciencia para jóvenes estudiantes de la Comunidad de Madrid celebrado durante los meses de mayo y junio de 2016. El coloquio contó con la presencia de los poetas y a la vez científicos (o viceversa), que había sido jurados del Certamen.

Entre los jurados se encontraba Antonio Córdoba Barba, ilustre matemático  y poeta que,  didáctico,  en el recital de poemas, sacó de un bolsón una banda de papel y relató las características geométricas de la cinta de  Moebius, recitando a continuación su magnífico poema homónimo. Luego con un tubo explicó y nos hizo imaginar esa figura mágica que es la botella de Klein.

Antonio Córdoba explicando la botella de  Klein

El público, embobado,  no daba crédito,  y escuchó sonriente el poema: “El círculo más vicioso / y la recta más coqueta, / se enrollaron    en     un tubo….” Fue un momento verdaderamente inolvidable para todos los que asistimos al acto.

Con motivo de la exposición actual sobre  Escher que se está realizando en Madrid,  Antonio Córdoba nos ha enviado una crónica de la misma en que recuerda la acto celebrado en septiembre y glosa y comenta sus poemas  Banda de Moebius benedettina y La botella de Klein, poemas ambos que se incluyen a partir de hoy en la sección poesía y ciencia. A continuación transcribimos el texto que nos ha enviado.

Escher y la Banda de Moebius

En La obra de Maurits Cornelius  Escher está de nuevo de moda  en Madrid debido a su exposición   en el palacio de Gaviria que, en cierto modo, es continuación de la que  tuvo lugar en las salas del Canal en el año 2012. La prensa se ha hecho eco  publicando las reflexiones y las impresiones que esos grabados de tan clara inspiración  geométrica han inducido en diversos autores.

Ahí tenemos las teselaciones (ángeles-demonios, cielo-infierno) que tan bien ilustran la geometría hiperbólica en ese modelo maravilloso que debemos al genio de Poincarè; las geometrías imposibles con sus bucles de escaleras, o canales acuáticos, que bajan y suben desafiando a la lógica y a la gravedad; sus intrigantes anamorfosis o esa espléndida galería de grabados, donde  podemos encontrar desde la acción de una transformación conforme hasta, sin forzar demasiado, la presencia de una curva elíptica.

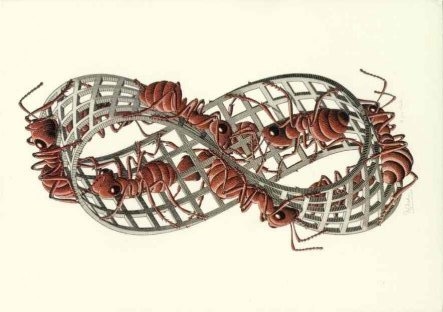
El universo plástico de Escher ha dado lugar a varias publicaciones en las que se ha analizado en profundidad su biografía y sus técnicas. Es pues muy difícil aportar una pizca de originalidad a un tema tan profusamente tratado. En nuestro caso vamos a intentarlo centrándonos en la banda de  Moebius, una superficie que fascinó a Escher y de la que nos legó varias imágenes, siendo quizás la más espectacular aquella en la que la banda es una rejilla por la que circula una fila de hormigas.

Supongamos que disponemos de una tira de papel (digamos que en forma de rectángulo cuyo lado mayor (horizontal) supera con creces al menor (vertical)), si ahora pegamos los lados menores sin someter el rectángulo a torsión alguna,  haciendo coincidir los vértices que están a la misma altura,  obtendremos un cilindro que tiene dos caras: exterior e interior.  Con un poco de imaginación podemos situar a unos seres bidimensionales, planitos, que vivan en esas caras, dando lugar a dos tribus distintas sin contacto posible: la única manera de pasar de una a la otra es algo traumática, practicando una perforación, ya que el borde del cilindro es impracticable para nuestros planitos. No obstante ambos mundos son orientables: un planito que disponga de un reloj (también planito ¡claro!) y que se mueva por la cara exterior verá siempre girar en el mismo sentido las agujas de su reloj. Y así ocurre también en la cara interior.

Peguemos ahora esos mismos lados pero haciendo la torsión necesaria para que el vértice superior de un lado se acople con el inferior del otro. La superficie que resulta es la célebre banda de Möbius y tiene una sola cara, como bien ilustra el grabado de Escher: las hormigas pueden recorrer todos sus puntos. No hay dos, sino una sola tribu: ¡fantástico, abajo fronteras y nacionalismos! No obstante, lo que se gana en unificación se pierde ahora en orientabilidad: un planito que siga el camino de las hormigas verá como el giro de las agujas de su reloj cambia a lo largo del recorrido. La banda de Möbius no es orientable. Esto da que pensar, pero mejor hacerlo en verso:

Banda de Moebius benedettina

Ya ves que ando escaso de dinero,
y nadie en el barrio me conoce.
Transparente resulto a las miradas
de las bellas que pasan junto a mí.

Pero ven, deja que te muestre,
mira y verás:

Si cortamos una cinta bien larga,
y pegamos sus bordes con cuidado,
surgirá un mundo de una sola cara,
donde alegres vivir desorientados.

Cuando el círculo se desliza en contacto con la recta, o cuando la recta se contonea abrazando al círculo, generan un cilindro. Si ahora pegamos los dos bordes circulares de ese cilindro (imaginemos que es un tubo de caucho, o de plomo, que podemos flexionar sin problemas) obtendremos una especie de “donut” o neumático, una superficie que los matemáticos llamamos “toro”.  Cabría hacer esa unión de manera algo más complicada dando lugar a diversos nudos. Pero si ese es nuestro proceder, conseguiremos siempre superficies que dividen al espacio en dos regiones, o mundos distintos, los de dentro y los de fuera.

Siguiendo la analogía con la cinta de Moebius  cabe preguntarse si hubiera una manera de pegar los dos círculos frontera del cilindro de manera que la superficie resultante tenga una sola cara, en otras palabras, que no divida al espacio en dos regiones separadas. Una posibilidad consiste en taladrar un orificio en el cilindro e introducir a su través uno de sus extremos  para unirlo luego por dentro con el otro. Se obtiene así un objeto curioso, una especie de botella compacta que carece de interior y que, como le ocurre a la banda de  Moebius, tampoco permite ser orientada.

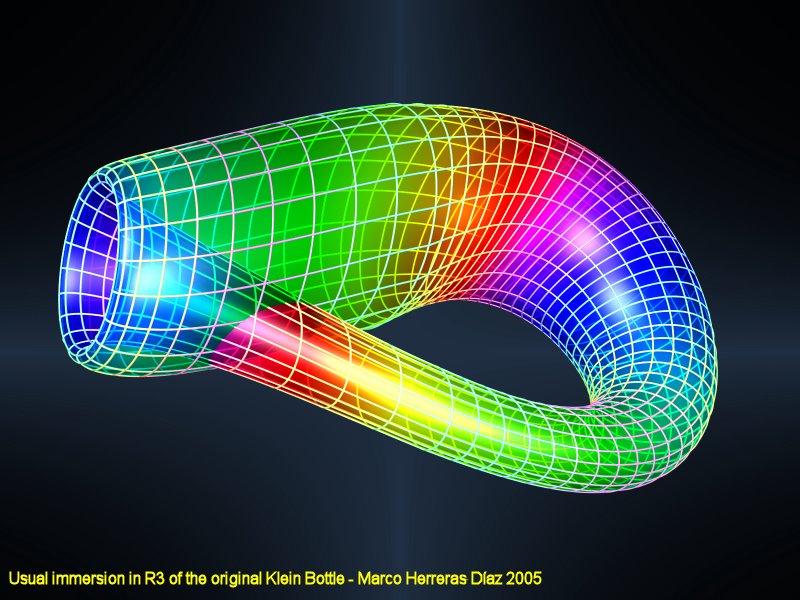
Una botella de Klein

Hay, no obstante, una pega que atañe a nuestra noción de superficie: cerca de cada punto el espacio tiene que parecer plano. Eso ocurre en casi todos los puntos de la botella, pero falla estrepitosamente en la cicatriz del orificio que hemos practicado, allí, por pequeño que sea el entorno que consideremos, el espacio no se parece (no es homeomorfo) a un plano. En realidad ese empeño es imposible dentro del espacio tridimensional, pero el gran Felix Klein se dio cuenta de que en 4 dimensiones sí podemos hacerlo.  El resultado es conocido como “La botella de Klein”.

La botella de Klein

El círculo más vicioso,
Y la recta más coqueta,
Se enrollaron en un tubo,
Embrión de la botella.

Compactos, sin penetrarse,
En una dimensión extra,
Confunden a quien desea,
Estar dentro, o quedar fuera

Antonio Córdoba Barba

Excelencia y pasión,  y entusiasmo y alegría como matemático,  como poeta y como gran divulgador de la ciencia.

Nuestro agradecimiento más sincero a Antonio Córdoba Barba.