![]()
Las Incertidumbres de la Ciencia: Ajustes a los Modelos de Regresión Estadística
El otro día, una carta en Nature Physics me llamó mucho la atención: “Laws, Power laws and Statistics” (por Mark Buchanan). La verdad me quedé un tanto sorprendido, debido a que era un mero resumen de otro trabajo publicado en abierto, que llevaba el titulo: de “Power-laws with empirical data”. Al parecer, a algunos redactores de esta prestigiosa revista les faltan las ideas. Eso sí, Mark especulaba con tal entusiasmo como el que descubre la dinamita. Sin embargo el problema existe, es muy serio y la solución difícil. Se trata de las conclusiones de estudios de investigación obtenidas cuando se ajustan datos a modelos de regresión. En este caso se hablaba tan solo de leyes potenciales, pero lo mismo podría decirse de todos los demás. El autor defiende que, a menudo una misma distribución se ajusta bien a varios modelos de regresión (lineales, exponenciales, logarítmicos, polinomiales, etc.). Generalmente no se testan todos (con frecuencia solo uno), por lo que se nos dice en muchísimas publicaciones debe ponerse en tela de juicio. Es cierto, no le en este sentido. Llevo analizando el problema desde hace muchos años, por cuanto trabajo con tales distribuciones estadísticas. Y nos relataba otra gran verdad: el problema estriba en que un buen ajuste requiere miles de datos empíricos, los cuales raramente suelen ser proporcionados por estudios empíricos. ¿Qué hacer en estas situaciones harto frecuentes? ¡He aquí el dilema!
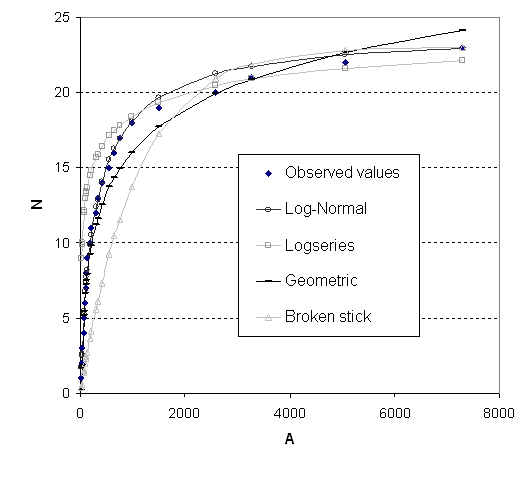
Ambigüedad de los datos de edafodiversidad de las
Islas del Egeo al ajustarse a 4 modelos de
distribución estadística. Los datos reales son los puntos
Fuente: Ibáñez, Caniego y San José, 2005. (Ecol. Model)
A partir de aquí el autor mencionado desbarra sobremanera. Al centrarse sobre una distribución potencial, lo único que señala es un problema muy concreto y una posible solución: la que ofrecen Clauset et al. (2007) en el último hipervínculo proporcionado. Si tuviera que valorar tan ramplón escrito y análisis, diríase que en Nature puede publicar cualquiera que se encuentre arropado por el establishment. Con toda humildad, he publicado en revistas de impacto sobre esta cuestión en varias ocasiones, escritos mucho mejores (en referencia a la revista mencionada), desconociendo que en Nature tenía una puerta abierta. Jajajaja, ¿alguien se lo cree? Pero vayamos al asunto.
Si usted tiene una base de datos y quiere analizar si se ajusta a un modelo de distribución, lo que demandan los cánones científicos es testar todos ellos. ¿Cuántos? Pues ni más ni menos que centenares, o potencialmente miles. El trabajo es más que ímprobo. De hecho, podríamos construir infinitos modelos de regresión, por lo que jamás sabremos si se ha detectado el mejor ajuste. Existe un programa en la Web (CurveExpert) que permite analizar el ejuste de los datos, simultáneamente, a decenas de estos constructos estadísticos. Se lo pueden bajar libremente. Una experiencia desconcertante para los novicios consiste en correr el modelo y observar que sus datos se ajustan significativamente a muchos de ellos. De hecho, este software nos ofrece un ranking de mejor a peor (dentro de los tipos de distribución estadística que contempla, por supuesto). Ok. Si la base de datos no es muy extensa, modifique un poco los resultados y vuelva probar. A menudo todo cambia. ¿Entonces que hacer?
Los borriquitos de la ciencia señalarían de inmediato que debemos abrazar el mejor ajuste y punto. Ahora bien, hablamos de borriquitos, no lo olvidemos. Resulta que este software utiliza un ajuste de mínimos cuadrados. Sin embargo, existen otros como el de Kolmogorov-Smirnov, que dicen los entendidos ser es más apto que el anterior, con vistas a tratar matemáticamente bases de datos pequeñas. Ahora bien, muy pocos lo utilizan, y si usted lo hace, se reducen drásticamente las posibilidades que tiene de comparar sus estudios con los de otros autores. Sin embargo si se repite el análisis con muchos modelos, el tes del chi-cuadrado y el de Kolmogorov-Smirnov, observará que el ranking cambia otra vez. Más aun existen otras alternativas con vistas a valorar la bondad de los ajustes estadísticos.
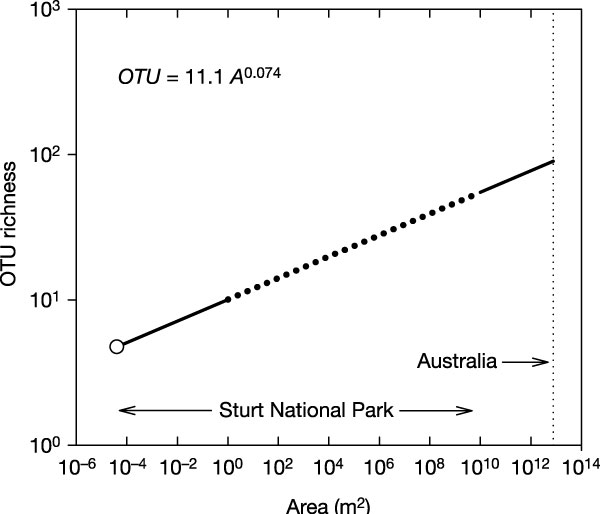
Ajuste ¿apañado? a una potencial de comunidades microbianas
de suelos desérticos de Australia. Fuente: Nature
Por lo tanto, nos encontramos que el investigador se encuentra frente a una tarea de titanes: cotejar su base de datos contra cientos de modelos y repetir tal iniciativa con varios test de ajuste. ¿Cuántos? No lo sé. Empero mañana puede salir al mercado otro test de bondad de ajuste, por lo que habría que retornar sobre sus propios pasos. Sin embargo, pueden también descubrirse las “maravillas” de nuevos modelos de regresión recientemente publicados. Por tanto el buen científico requeriría pasarse la vida ajustando los mismos datos a “tropecientos” productos estadísticos. Amigo Mark, así no funciona la ciencia, ni ahora ni nunca. Y no me digas chaval que el problema es que debemos trabajar con bases de datos enormes porque en la mayoría de los casos es absolutamente imposible obtenerlas. No te pases de listo.
A pesar de todo, permanece otro grave problema por resolver: ¡la calidad de los datos! Cuando se trabaja en un laboratorio el tema puede ser menos complejo, ya que siempre es posible detectar otra manera de acceder a otros mejores. Tan solo basta que mejore la instrumentación, por ejemplo. Ahora bien, los que solemos trabajar con bases de datos institucionales, elaboradas por muchos autores, conocemos bien la “calidad-precariedad” de la información que tenemos entre manos. Nunca es óptima. Por muchos modelos de interpolación que utilicemos, con vistas a mejorar la estructura espacial o el devenir temporal de la información, siempre hay incertidumbres. Y si además al cambiar algunas décimas de unos pocos (en un margen de precisión-incertidumbre aceptable en vista de los protocolos utilizados) nos topamos con que otros modelos se ajustan mejor, sencilla y llanamente lo mejor es pegarse un tiro en la cabeza. Así, conforme a este tipo de justicia divina: ¡todos muertos!
Les pondré tan solo un ejemplo. Por la razón que sea, no es inusual que cuando buscara ajustes a leyes potenciales me apareciera entre otras una distribución llamada Weibull. Mis datos se ajustaban a ella, muchas veces, mejor que a una potencial. Se trata de una ecuación mucho más compleja y difícil de interpretar. Llevemos tal incertidumbre a un Workshop y no se la prestó atención. Casi nadie la menciona cuando se habla de leyes potenciales o fractales. Pero un día se me ocurrió analizar en la Web y en Science Direct, año por año, cuantas veces aparecía en el transcurso del tiempo. Los resultados, según el análisis de la Web en bruto, o de las revistas indexadas, me dejaron atónito, por lo que serán motivo de otro jugoso post.
Resumiendo: Por mucho Nature que sea, Mark desbarra en su nota, mostrando una caricatura grotesca de un problema complejo y multifactorial. Existen incertidumbres intrínsecas a este tipo de análisis que son insoslayables. De hecho, casi todas las que menta este autor y muchas más, por supuesto. Entiendo perfectamente que aplicar el método de Clauset y colaboradores, para lajustar datos a las leyes de escala puede ser la mejor de las soluciones, hoy por hoy. Ahora bien, sigue sin excluirse la posibilidad de que los datos se ajusten bien a estas leyes u otras distribuciones estadísticas, así como que aparezcan en el futuro otros métodos que mejoren o refuten el propuesto por Clauset. Mark ha hecho una montaña de un grano de arena. ¿Por qué? Simplemente todo es debido a que a la hora de publicar no se dice todo lo que los investigadores han realizado, así como las incertidumbres que personalmente sufran ellos mismos. De hacerlo el artículo sería excluido, y aquellos castigados por ser honestos. Lo veremos en un post posterior.
Ahora bien, sí que entre tanto embrollo, están los que utilizan la estrategia de “a río revuelto ganancia de pescadores”. Desde luego, algo de orden si puede y debe ponerse en los siguientes casos.
1. Los resultados son muy diferentes si en una misma bases de datos utilizamos estos por individual (uno por uno) o acumuladamente (acumulando sus frecuencias paso a paso). Mi experiencia me dicta que, a menudo, datos de frecuencias acumuladas se ajustan mejor a una potencial que al tratarlos por separado. El investigador jamás debe escoger la forma de analizar los datos matemáticamente que le proporcionen los ajustes que más le convengan a la hora de corroborar su hipótesis de trabajo (cuando la tienen).
2. Agrupaciones de los datos empíricos de una base de datos en categorías o clases. Por ejemplo, si tienes para un archipiélago el número de islas y sus respectivas áreas, puedes analizarlos estadísticamente “individualmente” o agruparlos en unas pocas clases por rangos de tamaño (por ejemplo, menores de 1km2; entre 1 y 10 km2; entre 10 y 100 km2; etc.). Según los criterios de agrupamiento, un mismo grupo de datos puede ajustarse a una ley potencial o no.
3. El fraude científico: amañar la base de datos (eliminar por ejemplo los que “estropean” el ajuste) conforme a nuestros deseos.
Afortunadamente, el movimiento en acceso abierto que nos obligará a colgar de las Web de nuestras instituciones los datos brutos de los proyectos financiados por entidades gubernamentales, ayudará a separar el grano de la paja (aunque no siempre).
¿Cómo deberíamos clasificar este post? Miro las categorías y no se me “escurre nada”. Se admiten ideas que no sean ofensivas.
Juan José Ibáñez

Error de ortografía -> "¿Qué hacer en estas situaciones arto frecuentes? ¡He aquí el dilema!"
Debería ser:
"¿Qué hacer en estas situaciones harto frecuentes? ¡He aquí el dilema!"
Claudio, gracias. Luego hablo yo de borriquitos. Jajajaja.
Cordiales saludos
Juanjo
estoy justamente tratando de construir un modelo de correlación múltiple para tratar de medir el precio catastral en la ciudad de Ibarra, lugar de mi residencia de los bienes inmuebles, como un mejoramiento de la fórmula aplicada por el municipio, siendo las variables nuevas: nivel de ruido y contaminación del aire el método se llama precios hedónicos, como una tesis de grado para obtener el Ph.D, en Proyect Management en Atlantic International University, me gustaría oir sus consejos para tratar de hacer un trabajo científico de calidad. He realizado 730 mediciones en puntos seleccionados de la ciudad que se sectorizó en 25 lugares distintos, tengo la documentación respectiva que avala la información catastral real.