![]()
El Crecimiento de las Redes Sociales y su Estructura en Relación con las Redes Biológicas
Continuamos en este post analizando las redes complejas con especial énfasis en las sociales y las ecológicas. Hasta ahora nos hemos centrado esencialmente en sus estructuras y propiedades. Hoy hablaremos del crecimiento de Internet, así como en su resistencia a las perturbaciones. No obstante, como ya hemos mostrado, lo mismo ocurre con las redes biológicas (por ejemplo las metabólicas) y la estructura de los artefactos tecnológicos, entre otros muchos sistemas complejos, tal como el funcionamiento del cerebro. Os recordamos que, aunque cada post pretende ser un bloque de información individualizado, conviene leer los anteriores (ver al final del texto) con vistas a obtener una panorámica más completa. Comenzaremos hoy analizando la noticia aparecida en su día en El Mundo Digital y que llevaba por título: “El insaciable apetito de las redes sociales”. Seguidamente, analizaremos otras aun más interesantes. Iremos comentando una a una tras exponerlas. Iremos viendo como de la arquitectura y las formas de crecimiento de las redes complejas podemos extraer lecciones desconocidas por los ingenieros y científicos hasta fechas recientes.

Valerie Beller: Pintura sobre cluster de mundos pequeños
El insaciable apetito de las redes sociales
Más que una predicción, es un hecho. Las redes sociales en Internet han estallado y su inmensa popularidad hace que cada vez crezcan más, a pesar de las voces que alertan sobre ciertos problemas de privacidad para los usuarios.
FUENTE | El Mundo Digital; 27/01/2008
(…) Un informe de la compañía Experian sobre el impacto de las redes sociales, citado en el diario The Guardian, augura que este año las redes sociales se especializarán aún más -con ejemplos como SagaZone, de una aseguradora especializada en mayores- y comenzarán a desarrollarse herramientas para sacarles partido económico.
Según este informe, las empresas deben apresurarse a comprender y utilizar bien las herramientas de la llamada Web 2.0, ya que tienen capacidad de generar usuarios muy fieles.
Mientras tanto, esas herramientas van evolucionando. El informe predice que los sitios líderes o de referencia, como MySpace (alrededor de 300 millones de cuentas, y subiendo), Facebook (más de 52 millones de perfiles, y subiendo) o Bebo (más de 40 millones de usuarios, y creciendo) realizarán este año mejoras significativas en la búsqueda y organización, mientras (…).
POCAS REDES GRANDES, MUCHAS ESPECIALIZADAS
José Antonio del Moral, director de Alianzo y experto en redes sociales, predice un futuro inmediato con «cada vez más redes sociales temáticas y más interacción entre las redes sociales que ya existen«. Algo que, de hecho, ya está sucediendo.
«Al final, calculo que habrá dos o tres grandes redes sociales en todo el mundo», afirma. Una será de Google, otra en torno a Microsoft (probablemente con Facebook) y una tercera aún por determinar. Según Del Moral, en España, MySpace, la red más grande del mundo, «lo tiene muy difícil por la creciente presión que están ejerciendo los medios de comunicación, que tienen una gran capacidad (hasta ahora infrautilizada) para generar redes sociales con sus lectores/usuarios».
INVESTIGACIÓN
La mina que suponen las redes sociales va más allá del puro marketing, y suponen un material muy valioso para la investigación académica. Sociólogos de la Universidad de California (UCLA) y Harvard utilizan información de Facebook para diferentes análisis.
Las amistades que cada perfil genera, y las relaciones entre sí, se reflejan de una forma que no tiene precedentes, según Andreas Wimmer, profesor de Sociología en la UCLA. «Comparado con los datos de una investigación usual, es un paso adelante gigantesco en lo que respecta a la precisión en que las relaciones están registradas», comentó a la BBC. La recolección de este tipo de datos es, pues, más fácil que nunca (…).
VOCES DE ALARMA
No obstante, crece el número de voces de alarma sobre la peligrosidad de estas herramientas para la privacidad de los usuarios. La popular red Facebook se enfrentó hace un mes a las protestas de decenas de miles de usuarios al lanzar su herramienta publicitaria hace apenas un mes.
Bautizada ‘Beacon’, la herramienta enviaba mensajes a los ‘amigos’ de los usuarios en los que informaba acerca de sus compras ‘online’. La protesta de los usuarios hizo que la compañía ‘rectificase’ (…). Por su parte, la UE ya ha anunciado que vigilará con lupa las actividades publicitarias en la Red para preservar la privacidad. (..) José Antonio del Moral cree que el equilibrio entre privacidad y publicidad está en «respetar a las personas, sin olvidar tampoco que los gestores de redes sociales son empresas que también deben obtener beneficios económicos (…).Pero la privacidad depende también de uno mismo (…).
Autor: Pablo Romero
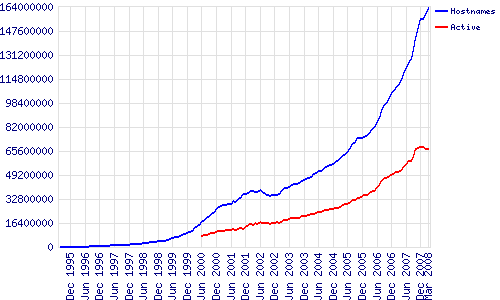
Crecimiento de Internet. Fuente: Tu función
Nodos activos en rojo y totales en azul
Un aspecto de la noticia a resaltar: por mucho que pretendamos generar un mundo igualitario, los sistemas complejos se rigen por una estructura y dinámica concretas. Ya cometamos en uno de los post precedentes que se ajustan a las denominadas curvas de Willis. Como ha indicado otro blogger, podría interpretarse recurriendo a la metáfora de la Ley de San Mateo: Quien más tiene más tendrá y a los más desheredados se les secuestrará. En otras palabras, Internet tiende a crecer conforme a la estructura de los mundos pequeños, pero también al seguir la susodicha ley, existirán muy pocas Webs súper-vinculadas y un número apabullante de otras cuya conectividad decrece de forma potencial. Volvemos a reiterar que lo mismo ocurre en las redes biológicas, por citar tan solo algunas, y no hablar por ejemplo de la emergencia de los ensamblajes de suelos etc. Pero veamos ahora que se nos dice en este enlace sobre el crecimiento de Internet. Del mismo modo, las Web super-vinculadas y de información general podrían asimilarse en ecología a las especies generalistas, mientras que las menos conectadas a las especialistas. Notad que utilizo el vocablo “podría”, ya que se trata de una mera conjetura sobre la que debemos reflexionar.
En la siguiente gráfica podemos ver el gran crecimiento pero también se aprecia el estancamiento de las denominadas «web activas» (se actualizan a diario), estas webs activas ya representan únicamente un 48% del total de sitios, lo que indica el gran número de sitios webs abandonados o que se utilizan únicamente porque aún generan ingresos publicitarios.
El crecimiento de Internet como se puede ver en las gráficas es imparable y en estos últimos años se duplica cada trienio:
2002 – 40 millones de sitios
2005 – 80 millones de sitios
2008 – 160 millones de sitios
Cierto es que el crecimiento en este último trienio ha sido debido en gran medida a la aparición de los blogs y redes sociales, que ponen al alcance de cualquiera la posibilidad de crear un sitio web

Interconectividad: Nodos hiperconectados y Hubs
Como ya avisa el autor, debemos tener cuidado con las cifras, ya que muchos nodos han desaparecido mientras que otros se encuentran en vías de extinción. Como en la evolución biológica, unas especies se extinguen (nodos) y otras aparecen. Debido a ello, podríamos obtener un exponente de crecimiento menor que el que se desprende de los datos de arriba y valores fraccionales. Ahora bien, continuando con el paralelismo evolucionista, cabe preguntarse si la emergencia de nuevos soportes y/o diseños en el ciberespacio (como blogs y wikis) equivaldría a los periodos o épocas geológicas en donde se produjeron irradiaciones explosivas de especies (generalmente tras otros que han padecido extinciones masivas como resultado de grandes perturbaciones o catástrofes. Pero si este fuera el caso, ¿Qué analogía en Internet debemos buscar para dar cuenta de estas últimas? Postulo que la Web es demasiado joven (un bebé), por lo que debe esperarse a que sufra perturbaciones e innovaciones de muy variable magnitud y frecuencia, con vistas a ue nos permitan precisar la existencia o no de tales singularidades. Pero sigamos, buscando más detenidamente. Hemos topado con un post clásico, escrito por David Ugarte en su blog Bitácora de las Indias. Nos referimos al titulado: “El Gran Apagón: El terrorista son las matemáticas. Con el entramos ya en materias más serias.
Gran apagón: el terrorista son las matemáticas
Martes, 19 de Agosto de 2003 – por David de Ugarte
El gran apagón norteamericano ha sido recibido con regocijo por la debilidad imperial entre la prensa española en papel y por reclamos de seguridad entre la liberal. Ambos se equivocan. ¡¡Son las matemáticas, estúpido!!
Tres líneas eléctricas en Ohio dejan de funcionar. En unas horas el sistema eléctrico de la región más rica del mundo colapsa. Cincuenta millones de personas se quedan a oscuras. Un escalofrío: ¿Terrorismo? No, ningún grupo terrorista hubiera podido saber dónde golpear para producir un efecto tan amplio. Ni siquiera lo sabían los responsables de la red eléctrica norteamericana. Lo que si sabían, al menos desde 1996, es que un apagón en cadena podría volver a ocurrir. La robustez y la vulnerabilidad de una red no dependen del equipamiento tecnológico sino de su arquitectura y ni siquiera son contradictorias. Robustez y vulnerabilidad son propiedades simultáneas en las redes complejas. El terrorista son las matemáticas.
En general, la forma en que la naturaleza obtiene robustez en un sistema es maximizando la interconectividad. También nosotros: basta echar un vistazo a la topología de internet. Cuando una red crece líbremente -como Internet, los enlaces en la web, el sistema aéreo o la red eléctrica- dejando que los nuevos nodos se conecten al nodo anterior que deseen, inevitablemente aparecen hubs, conectores que atraen a un mayor número de conexiones por el hecho de estar allí. Su efecto es minimizar grados de separación entre nodos, el número de pasos que hay que seguir para ir de una parte a otra de la red siguiendo las conexiones. Por ello, los conectores, al crecer tienen cada vez más atractivo sobre los recién llegados. Es el fenómeno conocido como conexión preferente. Si abro un aeropuerto en Cuenca lógicamente será más útil que los vuelos vayan a Madrid o Londres que a Reus, porque desde ahí los viajeros tendrán que hacer menos escalas para llegar a cualquier lado. Las redes de crecimiento libre (free scale networks), por este motivo funcionan de acuerdo a leyes potenciales cualquiera sea su tamaño.
¿Qué quiere decir ley potencial? Pues que si relacionamos el número de nodos (y) con el de enlaces que soporta cada nodo (x), nos encontramos con funciones del tipo y= k* x-n. Es decir, que el número de nodos que sólo tienen un enlace será una potencia del número de enlaces que soporta el nodo más conectado. Al exponente n se le llama el grado de la función.
Permítanme que haga un inciso. Ya hemos hablado en el post sobre la configuración de los mundos pequeños acerca de la robustez-fragilidad de las redes con tales características. Una frase de Ugarte (dentro de su excelente narración) puede y debe ser cuestionada.” la forma en que la naturaleza obtiene robustez en un sistema es maximizando la interconectividad”. Como ya hemos comentado en el post de nuestra propia cosecha al que he hecho referencia, la conectividad total torna a las redes complejas sumamente frágiles frente a perturbaciones aleatorias. La conectividad (interrelaciones) entre las especies de un ecosistema decrece conforme aumenta su biodiversidad. De no ser así. las comunidades biológicas colapsarían frente al menor impacto ambiental. Ahora bien las especies clave suelen estar muy conectadas con otras ¿Serían equivalentes a los hubs? En Internet ocurre lo mismo. De ahí que las topologías de los mundos pequeños desplazan a las de tipo aleatorio. ¡Cuidado!. Sin embargo tal topología no induce una tendencia a interconectarse al azar de sus nodos constitutivos, sino todo lo contrario. De ahí que algunos de estos últimos estén hiper-conectados, mientas que su número aumenta conforme desciende la cantidad de enlaces que atesoran. Preguntémonos de nuevo, ¿equivalen tales “hubs” a las especies clave de las que hablamos en un post anterior?
Pues bien, el profesor Shlomo Havlin, de la Universidad de Bar-Ilan, demostró en el 2000 que las redes con un grado menor de tres no pueden caerse (hay que retirar todos los nodos para que la red colapse). El dato es relevante: Estudios empíricos sitúan por ejemplo entre 2.1 y 2.6 el grado de la red de hiperenlaces de la WWW, por eso al retirarse los dos principales nodos de la web española (las versiones web de los dos mayores periódicos), las páginas web españolas sufrieron en su valoración por Google, pero no desaparecieron: la red española perdía valoración en conjunto porque tendía a convertirse en una isla dentro de la web global, aunque no se desintegrara interiormente.
Y es que la robustez no sólo es la propiedad de evitar una caída general. También es la medida de la resistencia local a un fallo. En este sentido, la robustez de las redes complejas en buena parte se debe a que si los errores afectan por igual a todos los nodos, como los conectores son pocos, las probabilidades de que un error afecte gravemente a un número amplio de nodos en una región determinada son también pocas. Esa es parte de la filosofía de la Internet original por ejemplo.
Sin embargo, como comentaba el Profesor Barabasi, de la Universiedad de Notre Dame (Estados Unidos), eliminar un cierto número de nodos puede convertir Internet en un conjunto de piezas aisladas (…) no es una consecuencia del mal diseño o de fallos en los protocolos de Internet, la vulnerabilidad a ese tipo de ataques es una propiedad inherente a las redes de libre crecimiento El profesor Duncan Watts de la Universidad de Columbia demostró que el punto crítico necesario para alcanzar el nivel en que una red se rompe es fácilmente alcanzable. Resultados similares se obtuvieron en la Universidad de Barcelona cuando los profesores Solé y Montoya estudiaron por primera vez en el 2000 la fragilidad de las redes ecológicas en un paper que es hoy referencia en todas las bibliografías científicas. Es decir, todos los estudios prácticos y estudios topológicos demuestran que en las redes complejas vulnerabilidad y robustez son dos propiedades inseparables.
En otras palabras, Ugarte nos advierte (como ya lo hicieron Montoya y Solé), y vimos al hablar de los mundos pequeños que la configuración de las redes complejas es resistente a los ataques aleatorios pero no a los que van dirigidos a los nodos hiperconectados.
¿Por qué ocurrió el gran apagón? ¿Pudo haberse evitado?
La red eléctrica es una red compleja en la que funcionan todas las observaciones de la teoría de redes. Tiene sin embargo una diferencia con otras redes: cuando un nodo cae, su carga se redirige automáticamente hacia otros nodos cercanos. Si estos tienen capacidad no usada podrán absorberlo sin problemas y el apagón será local, sólo perceptible por aquellos que tomen electricidad directamente del nodo caído. Si no es así se producirá un fallo en cascada que sólo terminará cuando los nodos receptores tengan capacidad excedente suficiente. Un fenómeno así fue exactamente lo que ocurrió a partir del fallo en Ohio.
Demos por hecho que los fallos locales son inevitables. El objetivo sería reducir las caídas en cascada. El último fallo en cascada del sistema eléctrico norteamericano fue en 1996, se originó en Denver y afectó al mediooeste americano. Entonces, como ahora, los políticos y los creadores de opinión intentaron sacar lecciones. Se redobló la inversión en infraestructuras aumentando el margen de carga no utilizada por las líneas. Pero las caídas en cascada son también un viejo amigo de la teoría de sistemas dinámicos: desde la economía a la memética, la magia del Tipping point fascina. Sabemos que los procesos que llevan a un fenómeno de cascada son durante cierto tiempo invisibles. Un tiempo que es proporcional al margen de sobrecarga de la red.
Pero vayamos por partes: El Tipping point es el punto en el que se inicia un proceso de cascada. Una explosión nuclear por ejemplo un proceso de cascada que inicia con un tipping point (el momento en el que se alcanza la masa crítica). El proceso mediante el que se llega a un tipping point sigue en si mismo la estructura de una red en crecimiento y por tanto se somete a una ley potencial.
Una nueva venganza de las matemáticas: al incrementar proporcionalmente los márgenes de resistencia, las sobrecargas transferidas aumentan potencialmente al ganar la cadena nodos equivalentes: una vez alcancemos el Tipping point las sobrecargas que enviemos al resto de la red serán mucho mayores y el proceso por tanto más rápido.
Por ejemplo, imaginemos que el problema se origina en una subred formada por nodos que soportan flujos de hasta 5 unidades y que habitualmente soporta 3 en el que cada nodo se conecta con otros tres iguales antes de salir a la red nacional. Un nodo de repente soporta 6 (un incremento del 20% sobre el máximo) quedará anulado y transferirá sus 6 unidades de carga a los otros tres, que la absorberán sin que se inicie un proceso de cascada. Estamos en el límite, una pequeña diferencia en la sobrecarga (de 6 a 7) y se caerán todos los nodos, enviando a la red nacional 16 unidades de carga (7+3+3+3). Ahora subamos el margen medio no utilizado de la subred hasta un 100% de la carga media soportada, cada nodo soportará un máximo de 6 unidades de carga. Un nodo tirará la red a partir de saturarse con más de 9 unidades de carga, por lo que cuando nuestra subred caiga lanzará a la red 19 unidades de carga.
No es difícil, a partir de este ejemplo entender las consecuencias. Caídas en las subredes locales cuyos márgenes se han ampliado producen efectos más que proporcionalmente mayores al salir a la red nacional. Si no se hubiesen aumentado los márgenes de resistencia individual de algunas subredes, pequeñas sobrecargas harían saltar los plomos localmente y hubieran permitido gestionar la crisis. Si este apagón ha tenido mayor amplitud y duración que el de 1996 ha sido precisamente por las medidas que entonces se tomaron para evitarlo. Al aumentar los márgenes de sobrecarga de las zonas más pobladas aumentaron el nivel de error necesario para alcanzar un Tipping point y en consecuencia hicieron crecer más que proporcionalmente el número de clientes finales afectados y el espacio físico cubierto por la red. Pero sobre todo el tiempo durante el cual el problema fue invisible a los técnicos. Y es que cuando no se las tiene en cuenta, las matemáticas pueden ser el peor terrorista.
Nada que objetar, dentro de lo que puedo discutir, por cuanto no he leído parte de los textos que cita Ugarte. Cuando se refiere a que “las matemáticas pueden ser el peor terrorista, nos indica que los ingenieros deben aprender mucho de los análisis de las redes ecológicas y sociales a la hora de diseñar sistemas robustos. La ingeniería clásica ofrece mucho menos. Las investigaciones sobre redes complejas ayudarán a formular nuevas teorías de diseño, no lo duden. Terminemos remarcando que si la magnitud-frecuencia de los fallos en una red se ajustan a una ley potencial, entramos en otro ámbito de las ciencias de la complejidad denominado “Teoría de la Criticalidad Autoorganizada”. Sin embargo, reconozco que encuentro problemas para encontrar analogías entre ciertos aspectos de las estructuras de Internet y las redes biológicas. Por ejemplo, ¿a que equivalen las hubs en una red ecológica? Os lo pregunto a vosotros. Veamos si hay interactividad entre este blogger y los pocos sufridores que le leen.
Material relacionado
Crecimiento de Internet
http://www.tufuncion.com/crecimiento-internet
Crecimiento de Internet, Leyes potenciales y el gran apagón
http://www.lasindias.com/articulos/network_theory_agosto.html
http://www.eduteka.org/Web20Ideas.php
Crecimiento de Internet y fractales (14.000 citas en Google)
http://elnido.ech.es/N23/mundocuantico.htm
La ‘edad de oro’ de las redes sociales en la Red
Sobre el artículo de Barabasi, las Hubs y los ataques de Internet
Sobre los Hubs y los ranking en Internet
Otros post Previos Relacionados con el Tema
Redes Complejas: Redes Sociales y Redes Ecológicas (Los Mundos Pequeños)
Conectividad, Redes Sociales y Redes Ecológicas
Especies Clave y Nodos Clave: Redes Ecológicas, Redes Sociales
Continuará…………
Juan José Ibáñez

[…] El Crecimiento de las Redes Sociales y su Estructura en Relación con las Redes Biológicas […]