![]()
Textura del Paisaje y Lagunaridad (Lacunarity)
En un post previo, al hablar de la aplicación de los fractales al estudio de la distribución de tipos de suelos en Europa (mediante el uso de tecnologías SIG), detectamos para nuestra sorpresa que todos ellos se dispersaban por el continente de acuerdo a una estructura fractal. Sin embargo, ya una rápida inspección visual de los mapas de cada taxa mostraba que existían diferencias conspicuas de sus patrones espaciales. El trabajo ya se encuentra en vías de publicación, pero los autores (este impresentable administrador, Rufino Pérez y Fernando San José, ambos de la UPM), nos quedamos con un sabor agridulce. Buscando las razones de aquellos resultados topé con el concepto e índices para estimar la lacunaridad. Obviamente, todo aquello era muy reciente y yo me había quedado obsoleto con mis conocimientos de la ecología del paisaje de finales de los ochenta y principios de los noventa. Al parecer, vamos a retomar los análisis y, en consecuencia os escribo un post explicando el interés de estimar la lacunaridad, en los estudios sobre fractales, análisis de imágenes y ecología del paisaje y geografía de suelos. Por lo que podréis leer abajo, el propio Mandelbrot detectó esta falta de sensibilidad de los análisis fractales e inició esta línea de investigación. Estos índices resultan ser muy útiles con vistas a determinar la porosidad de los paisajes (heterogeneidad o discontinuidad de la estructura), siendo un buen complemento de los de fractalidad, aunque puede emplearse también en ausencia de las invarianzas a los cambios de escala.
Efectivamente, la lacunaridad (o lagunaridad) cuantifica la estructura espacial de los espacios vacíos de una imagen, ya sea fotográfica o de un mapa, bidimensional o tridimensional, según sea el caso.

Análisis de la lagunaridad de un bosque con especies
arbóreas que se distribuyen diferencialmente: Fuente Match Análisis
for ARC/GIS; Young forest is yellow, mature conifer green, mature
mixedwood brown, and water is blue (Classified Landsat image-
Northwest Ontario, in an area north of active logging).
Como se dice más concretamente en el primer enlace de abajo puede usarse para determinar las diferencias en la textura de los objetos de estudio que atesoran idénticas o parecidas dimensiones fractales. Pero también con otros motivos, como os exponemos en las ilustraciones de análisis demográficos y urbanísticos. Cuando se aplican herramientas SIG habrá que recorrer la imagen con ventanas móviles y hacerlo (como en el caso de los fractales) estimando cuadrículas a diferentes niveles de resolución. Personalmente, recomiendo tres órdenes de magnitud si lo que se intenta es averiguar también la posible invarianza de escala. Como veréis en los fragmentos de textos que recojo abajo, conviene acotar muy bien el área de estudio. Por ejemplo, si en un mapa o una imagen “lo que” pretendemos estudiar se centra en una parte de la misma y no se halla dispersada por toda, debe acotarse la primera y eliminar todo lo sobrante, so pena de obtener datos sin sentido. Para los interesados que teman las matemáticas tan solo señalar que muchos de los SIG actuales o disponen de operadores concretos para su cuantificación o es sumamente sencillo introducirlo haciendo uso de otros que ya existen en el software. En la Web inglesa se ofrecen muchos ejemplos (pero no por desgracia en la española).
Aunque el tipo de generalizaciones que voy a realizar debe tomarse con precaución, digamos que la lacunaridad indica si una imagen (paisaje, mapa) es más heterogenea a una escalas que a otras. Del mismo modo, un fractal tiende a ser más lagunar (poroso) que otro si alberga mayores espacios vacíos. Por esta misma razón, puede ser una herramienta muy útil para analizar la porosidad de un suelo y por tanto su comportamiento hidrológico, como podéis observar en la foto de la Universidad de Tennessee de Edmund Perfect, muy conocido por Fernando San José y este impresentable administrador, debido a que es uno de los científicos que suele editar los artículos que se publican tras los Workshop que realiza sobre temas fractales Miguel Ángel Martín y colaboradores de la UPM (Pedofract, y a los que por supuesto Don Edmundo también asiste). Os dejo pues con mas información, tanto en inglés, como en castellano. Buena parte de la primera procede de un artículo del geógrafo Severino Escolano de la Universidad de Zaragoza. Más concretamente se trata de este, cuyo enlace ya lo hemos colocado en el texto.
La medida de la segregación residencial urbana: análisis multiescala mediante índices de lagunaridad
Severino Escolano Utrilla
Departamento de Geografía y Ordenación del Territorio. Universidad de Zaragoza
C/ Pedro Cerbuna, 12. 50009 Zaragoza. España
Análisis de las Texturas: Un aspecto importante del estudio de imágenes son los análisis de texturas. El análisis de imágenes reporta (….) que sólo con un parámetro no es posible diferenciar bien las texturas, pues diversas texturas con igual dimensión fractal tienen distinta apariencia. Algunos autores han desarrollado el concepto de lacunaridad para complementar el cálculo de dimensión. (…). Posteriores algoritmos se han desarrollado para mejorar los cálculos con ahorro de tiempo y mas casos diferentes abordados. ( ….).
La lagunaridad es una medida analítica multiescala de la heterogeneidad de una textura espacial. La propiedad multiescala y la capacidad para retener los patrones espaciales la convierten en una técnica alternativa útil para trazar la trayectoria temporal y espacial de la segregación, y relacionar sus valores con otros procesos sociales, económicos, culturales y espaciales. (…) Los resultados muestran que la lagunaridad es una medida consistente que refleja la variedad de patrones espaciales a todas las escalas, incluso aunque cambien las unidades espaciales de análisis.
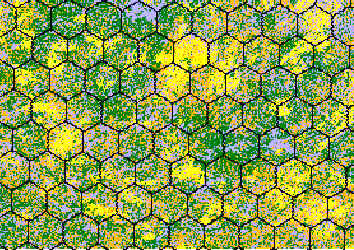

Análisis de la lagunaridad de un bosque con especies
Arbóreas que se distribuyen diferencialmente: Fuente Match Análisis
for ARC/GIS: Observar el las ventanas con polígonos de tamaño dispar
He traducido, de forma directa y rupestre, el término inglés “lacunarity” por el vocablo lagunaridad, que no existe en español. He preferido hacerlo así puesto que el resultado guarda gran parecido en su grafía y sonido con el inglés, que ya tiene carta de naturaleza en la bibliografía científica. En su lugar, tal vez se podrían utilizar sustantivos como discontinuidad o porosidad, aunque este último no parece adecuado para describir los vacíos de los objetos dispuestos en una línea.
Los índices de lagunaridad pueden constituir un método alternativo para medir la heterogeneidad de la textura de las distribuciones espaciales a varias escalas.
La noción de lagunaridad fue propuesta por Mandelbrot (1982) como una medida complementaria para caracterizar estructuras geométricas con la misma dimensión fractal, pero con diferente textura. La lagunaridad, que deriva del vocablo latino “lacuna”, es una medida de la distribución de los espacios vacíos en una estructura geométrica; en términos más precisos: la lagunaridad mide la desviación de una estructura geométrica de una invarianza traslacional (Gefen et al., 1983). El uso de ésta medida ha desbordado su marco original y se utiliza también para describir estructuras no fractales. En términos generales la lagunaridad es una medida analítica multiescala de la heterogeneidad o textura de una distribución espacial (Plornick et al., 1993).
En efecto, los índices de lagunaridad se han empleado para caracterizar configuraciones espaciales en diferentes disciplinas, como la biología y la medicina (Losa et al., 2005), y especialmente en ecología del paisaje, en cuyo ámbito además se ha realizado evaluaciones metodológicas de la lagunaridad y otras medidas multiescala (Plotnick et al., 1996; Dale, 2000; Peralta y Mather, 2000; Saunders, 2005).
Más fundamentales son las variaciones de la lagunaridad causadas por los componentes y relaciones que intervienen en su cálculo. La lagunaridad es una función de la distribución geométrica de los objetos en el espacio, de la fracción ocupada de un espacio dado, y de la escala en que se mida (Plotnick et al., 1993 y 1996; Dale, 2000).
Es lógico suponer que la resolución de las unidades espaciales de análisis influirá en las variaciones de la lagunaridad, en tanto que puede modificar la geometría de los objetos, una de las fuentes de variación de esta medida. No se han llevado a cabo aún investigaciones para conocer la dirección y alcance de esta influencia en el tema que nos ocupa.

Análisis de lagunaridad de espacios urbanos.
Metodología y datos
Se han desarrollado varios métodos para calcular la lagunaridad de la textura de un objeto, tanto si se trata de elementos distribuidos en un transepto, en una superficie o son de naturaleza volumétrica (Mandelbrot, 1982; Gefen et al., 1983; Lin y Yang, 1986; Tolle et al., 2003). Desde el punto de vista operativo el algoritmo más utilizado es el de “ventanas móviles”, propuesto por Allain y Cloitre (1991) y difundido a partir del trabajo de Plotnick et al., (1993). Por lo demás, este procedimiento está implementado en la mayoría de los programas informáticos dedicados al análisis de imágenes, y en los sistemas de información geográfica (SIG).
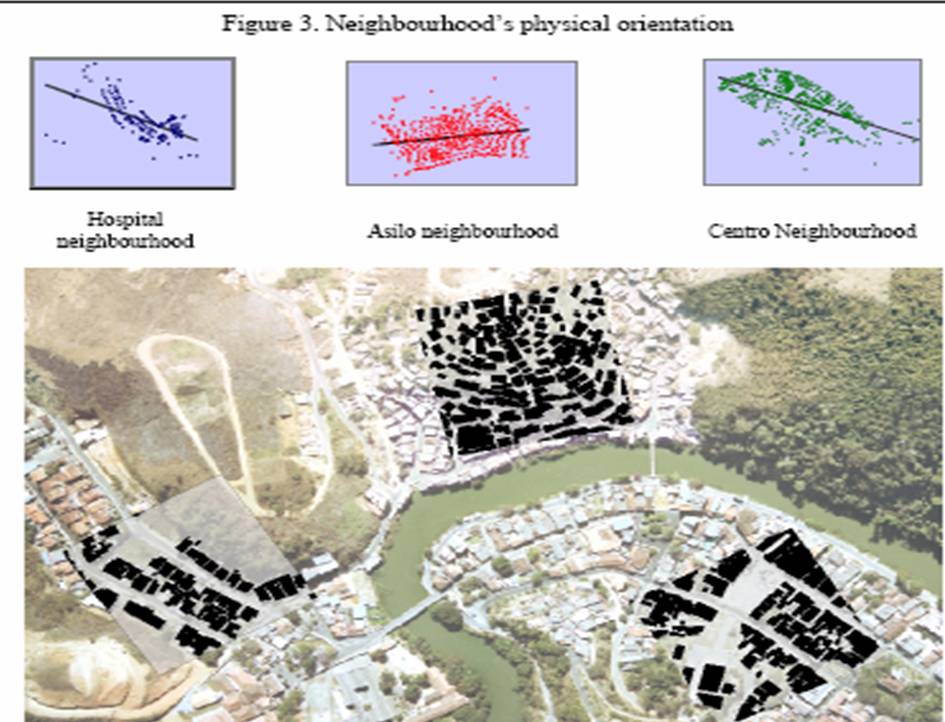
Análisis de lagunaridad de espacios urbanos.
Fuente: extraido del pdf a final de la página CASA
El método consiste en situar una ventana de dimensiones r x r (r=2) en el píxel superior izquierdo de una imagen de tamaño M, y obtener la “masa” (S) correspondiente a esa ventana. Si se trata de una imagen binaria la masa equivale al número de píxeles ocupados, es decir los que tienen valor 1; si es una variable continua, la masa se puede obtener con la suma de los valores. A continuación la ventana se mueve a la siguiente columna de la primera fila y se calcula de nuevo la masa de la ventana para esa posición. La operación se repite para todas las filas y columnas de la imagen. Con los datos registrados se construye la distribución de frecuencias de las masas de la ventana n(S,r); esta distribución de frecuencias se transforma en una distribución de probabilidad Q(S,r) dividiendo cada valor de frecuencia por el número de ventanas N(r).
Q (S,r) = n(S,r) / N(r) N(r) = (M – r+1)2
El primer y el segundo momento, Z(1) y Z(2), de esta distribución se definen:
Z(1) = S SQ (S,r)
Z(2) = S S2Q(S,r)
La lagunaridad expresa la relación entre estas dos magnitudes:
?(r) = Z(2) / Z2 (1)
El primer momento se puede describir también por la media aritmética, E(s), y el segundo por la varianza, Var(S), de las masas:
Z(1) = E(S) Z(2) = Var (S) + E2(S)
Como resultado la lagunaridad se expresa (Plotnick et al., 1993, 202-204):
?(r) = 1 + (Var (S) / E2(S)
Sin embargo, una sola medida de la lagunaridad obtenida a partir de una ventana móvil de un único tamaño es insuficiente para retener las variaciones multiescala de la textura de un objeto, y carece de valor para comparar diferentes configuraciones espaciales. Precisamente, una de las ventajas de esta medida se encuentra en la posibilidad de tener una colección de índices calculados para ventanas de varios tamaños con el mismo método antes descrito (Plotnick et al., 1993, 204).
Analisis de la Porosidad del Suelo mediante índices de lacunaridad
Fuente: Universidad de Tennessee (Edmund Perfect studies)
Es importante advertir que para obtener datos correctos es necesario delimitar el área de trabajo mediante un polígono o una hoja raster cuando se aplican las funciones de vecindad, o de lo contrario las ventanas móviles extienden los valores calculados más allá de la zona original de estudio, lo que produce resultados inconsistentes en los índices de lagunaridad. Por la misma razón es conveniente minimizar las áreas “sin datos” dentro de los límites del estudio. Esta restricción no se explicita en el citado artículo de Wu y Sui.
De acuerdo con la definición matemática de Lagunaridad, la cual es proporcional a la razón de la varianza respecto al promedio al cuadrado de un conjunto de datos (…) resultó apropiado para estimar la homogeneidad de la distribución espacial de la porosidad (…) así también la amplitud de lagunaridad varía según la resolución de cada fuente de datos geofísico y se manifiesta como una herramienta complementaria a las estimaciones de la dimensión fractal en los problemas de caracterización estática de yacimientos.
El movimiento y la distribución de fluidos a través de los medios porosos están determinados por su geometría. La naturaleza autosimilar de la estructura de estos medios ha sido el objeto de numerosos estudios que han documentado las relaciones de potencia (‘power law’) entre las principales medidas de poros y sólidos, y la resolución del método utilizado para su análisis. En la presente investigación se introduce un esquema fractal para clasificar los yacimientos naturalmente fracturados (YNF) a partir de imágenes de tomografía computarizada de rayos X. Esta clasificación tiene como propósito extraer y medir algunos rasgos geométricos de los poros tanto a nivel global (firmagrama), como local (líneas de referencia) vía los clasificadores fractales. Los clasificadores fractales, extraídos de las imágenes digitales, fueron útiles para hacer un diagnóstico simple y rápido del tipo de porosidad de un núcleo a partir de su imagen. La dimensión fractal de masa (Dm), la dimensión espectral o fractón (.d), el exponente de Hurst (H) y la lagunaridad ( Ë) de los YNF del sureste de México, son estadísticamente diferentes para los tres patrones de porosidad representativos de estos materiales: fracturas, cavidades y porosidad mixta. Para estimar los primeros dos (Dm y .d), es necesario presegmentar la imagen en conjuntos de poros y sólidos, creando una imagen binaria, previo a la cuantificación fractal. En los últimos (H y Ë), la extracción de los parámetros se realiza directamente a partir de las imágenes originales evitando el proceso de segmentación, lo que permite proponer a los clasificadores H y Ë como estimadores más confiables de la porosidad de los YNF. Todos los clasificadores fractales, y en especial la dimensión fractal de masa y la lagunaridad de los tres patrones de porosidad arriba especificados, mostraron una correlación estadísticamente significativa con la porosidad (medida con técnicas tradicionales) de las capas geológicas con distinta capacidad productora de hidrocarburos. Este hecho abre un nuevo panorama para la modelación y pronóstico de la geometría de los YNF
Página Web sobre lagunaridad de Eric Rauch
Chris Butson’s Lacunarity Page
Lacunarity is a counterpart to the fractal dimension that describes the texture of a fractal. It has to do with the size distribution of the holes. Roughly speaking, if a fractal has large gaps or holes, it has high lacunarity; on the other hand, if a fractal is almost translationally invariant, it has low lacunarity. Different fractals can be constructed that have the same dimension but that look widely different because they have different lacunarity. There are applications of lacunarity in image processing, ecology, medicine, and other fields.
(…) Lacunarity is a notion distinct and independent from D; it is not related with the topology of the fractal and needs more than one numerical variable to be fully determined. Lacunarity is strongly related with the size distribution of the holes on the fractal and with its deviation from translational invariance; roughly speaking, a fractal is very lacunar if its holes tend to be large, in the sense that they include large regions of space
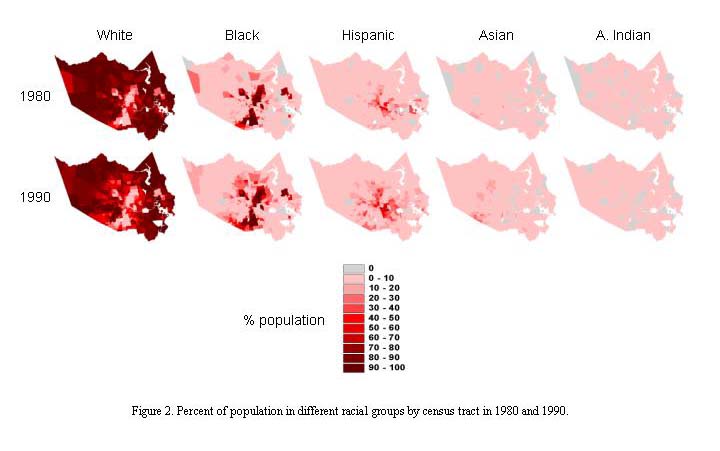
Análisis de la procedencia de la población en una ciudad
Mediante índices de lacunaridad y GIS. Fuente: ESRI
Lacunarity analysis is a multiscaled method for describing patterns of spatial dispersion. It can be used with both binary and quantitative data in one, two, and three dimensions. Although originally developed for fractal objects, the method is more general and can be readily used to describe nonfractal and multifractal patterns. Lacunarity analysis is broadly applicable to many data sets used in the natural sciences; we illustrate its application to both geological and ecological data. © 1996 The American Physical Society.
Lacunarity: Lacunarity is a multiscale metric describing the texture of spatial patterns. It is applied to a binary description of the landscape, such as forest/non-forest or conifer/non-conifer. In terms of ecological significance, lacunarity relates strongly to dispersal processes, in which the ability to move among habitats is related to the distribution and size of habitat and non-habitat patches. It is also important for describing the availability of ‘interior’ habitat across spatial scales.
The lacunarity metric essentially describes the distribution of gap sizes, with a landscape being more lacunar if gap sizes are distributed over a broad range (e.g., containing both large and small gaps). Lacunarity is low when gaps are distributed over a narrow range of values -i.e. gaps are of similar size. It thus measures the ‘gappiness’ or ‘hole-iness’ of a geometric structure (Plotkin et al. 1993). Gaps are assessed by using a ‘moving window’ that quantifies the relative amount of habitat within a window of fixed size moved systematically across the map.
It is useful, however, to assess lacunarity across a range of scales, by using analyzing the landscape with a series of windows of progressively larger sizes. The shape of lacunarity curves across a range of scales provides insight as to whether a landscape is more heterogeneous at fine scales, coarse scales, or if the landscape structure is independent of scale. Plotkin et al. (1993) point out that the shape of lacunarity curves are relatively insensitive to the number or density of gaps in the landscape; given the same basic size distribution of gaps, sparsely occupied landscapes will have similar curves to densely occupied ones.
In our analysis, we assessed lacunarity in three categories: forest/non-forest, conifer/non-conifer, and deciduous/non-deciduous. Window sizes began at 2×2 pixels (30 m pixels from Landsat classification), and were increased across 9 powers of 2 (4×4, 8×8, 16×16¼) to a maximum of 512×512 (29) pixels. In terms of hectares, box sizes ranged from 0.3 ha to approximately 21,300 ha. Lacunarity was assessed for each of the 9 subsections.
Because of the wide range of sizes used in lacunarity analyses, results are typically presented as logrithmic graphs, specifically ln lacunarity vs ln box size. This simply makes the curves more linear, and aids in visual interpretation of the graph.
The relationships between forest and deciduous lacunarity were very similar across all subsections; they differed in that deciduous lacunarity values were slightly higher than those for forest (Figure 9). Both were significantly lower than lacunarity based on conifer/non-conifer comparisons. In both forest and deciduous, the
(…)The patch size distribution and lacunarity analysis show that there are strong differences among subsections in terms of the ‘grain’ of the landscape. “Grain’ of course, is quite species specific – what is fine-grained to one species might be quite coarse-grained to another. Furthermore, grain as reported in this study is closely related to the source data – the minimum mapping resolution of Landsat data is 30 m, and these pixels were aggregated during the smoothing operations – there are likely very few polygons smaller than 1 ha.
Conclusions on landscape grain or texture need to be considered in light of these qualifications. Given these caveats, the study revealed differences in spatial structure among subsections.

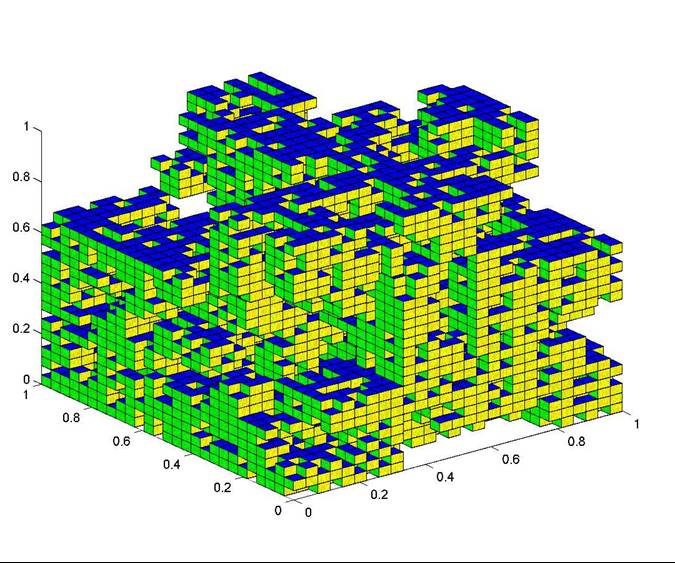
Tres cubos con ligeras diferencias en lacunaridad
Fuente: Universidad de Arizona
Lacunarity analysis is a multiscaled method for describing patterns of spatial dispersion. It can be used with both binary and quantitative data in one, two, and three dimensions. Although originally developed for fractal objects, the method is more general and can be readily used to describe nonfractal and multifractal patterns. Lacunarity analysis is broadly applicable to many data sets used in the natural sciences; we illustrate its application to both geological and ecological data. © 1996 The American Physical Society.
Juan José Ibáñez

[…] la distribución espacial de todos los edafotaxa presentes en Europa, con vistas a analizar si los índices de lacunaridad aportaban información relevante a la hora de caracterizar las texturas de sus respectivos […]
[…] Textura del Paisaje y Lagunaridad (Lacunarity) […]