![]()
El Dudoso Estatus de los Modelos de Simulación Predictivos en la Filosofía de la Ciencia
Un día, hace muchos años, leyendo un libro divulgativo sobre teoría de catástrofes, se me quedó grabada una frase del autor, que venía más o menos a decir: “El problema no es que los científicos experimentales jueguen con los modelos matemáticos, y aún que los construyan, sino que se los terminan creyendo”. El autor defendía la práctica de formalizar los conocimientos rigurosamente, para lo cual son de suma importancia, ahora bien, luego se intentan vender sus resultados como “veraces” cuando en la mayoría de los casos distan mucho de representar lo que realmente ocurre en la naturaleza. He intentado esquivar escribir este post por razones obvias. Cuando actualmente se habla de modelos de simulación predictivos, a todos se nos vienen a la cabeza los referentes al cambio climático. Sin embargo existen similares problemas en los elaborados por expertos de otras muchas otras disciplinas, como ocurre en edafología. Existen muchas razones palmarias para evitar a toda costa no confundir los hechos con los resultados de las predicciones. Sin embargo, numerosos de sus arquitectos, la prensa, e incluso las revistas científicas parecen preferirlos a los estudios que se realizan con datos de campo, “están más de moda”. En este post abordaré el tema, si bien existen muchas clases de modelos y cada uno con sus respectivos problemas. En consecuencia no podré más que plantear el tema con algunos ejemplos. Ya veremos vuestra reacción.

Rene Thom: Padre de la
Teoría de Catástrofes
Cuando uno comienza a hablar de modelos (algún día entraré a fondo en el tema) los oyentes siempre suelen asociarlo a complejas ecuaciones y constructos matemáticos que intentan predecir como se comportará determinado objeto o recurso, ya sea natural o artificial, en un futuro más o menos próximo. Sin embargo una hipótesis o un teoría ya son en si mismas modelos “conceptuales” pero modelos al fin al cabo. Y sobre ellas se ha edificado la ciencia durante siglos. Estos constructos no resultan ser más que simplificaciones de la realidad que intentan emularla haciendo uso de unas pocas variables entre el marasmo de todas aquellas que pueden afectar al objeto o proceso de estudio. Por tanto, son las premisas de sus arquitectos y no el “batiburrillo” del desarrollo matemático a que dan lugar la clave de su éxito o fracaso. Existen una enorme variedad de modelos, como por ejemplo: cualitativos, cuantitativos, deterministas, probabilísticos, predictivos, posdictivos, (…).
Desde un punto de vista formal, se considera que los deterministas, es decir los basados en sistemas de ecuaciones diferenciales, son los más elegantes y sofisticados. Sin embargo, en la naturaleza, a menudo resulta imposible aplicarlos, por los que se acude a los probabilistas. En la práctica, numerosos constructos de esta catadura son mixtos, por lo que no tienen cabida en el grosero bosquejo de clasificación al que aludí en el párrafo anterior. Pero ya es hora de entrar en materia.
Cuando más complejo es un problema a modelizar, generalmente porque intervienen muchas variables, y a menudo interaccionan entre ellas, tanto más difícil resulta que el constructo tenga éxito. Acertar con las variables clave puede terminar siendo en la práctica como buscar una aguja en un pajar. Digamos que los modelos reflejan el estado de conocimiento de una comunidad científica en un momento dado, por lo cual, desde el punto de vista de la filosofía de la ciencia, queda implícito que en el mejor de los casos podría refutarse, pero no decir que representan fielmente la “realidad”. Ahora bien, más tarde o más temprano se constatará que “fallan” (a no ser que formalicen triviales), siendo sustituidos por otros, y así ad nausean. La cuestión estriba en que una y otra vez, durante un lapso de tiempo concreto, ayuden a predecir algo “adecuadamente”.
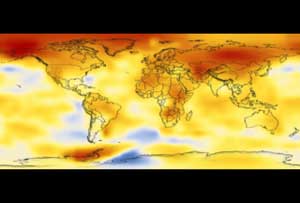
Salida de un modelo de circulación general de la atmósfera
Sin embargo, ya en primera instancia aparecen dos tipos de problemas, al menos en recursos naturales. El primero es la universalidad del producto y el segundo si se pueden corroborar o refutar en la práctica, de tal modo que cumplan su propósito. Así por ejemplo, de un modelo que realice predicciones a 40 años dudosamente puede decirse que es refutable o corroborable (soslayando los problemas que muchas escuelas filosóficas han detectados en estos conceptos poperianos). La razón estriba en que cuando se alcanza el umbral temporal de la predicción, ya se han elaborado otro sinfín de ellos más refinados, por cuanto la ciencia ha progresado desde su formulación. De esta forma, en ciertas especialidades abundan publicaciones que presentan estos productos sin que se pueda decir nada al respecto sobre sus bondades o debilidades, con la excepción de que existan problemas formales detectables e intrínsecos a los mismos. Muchas veces los más verosímiles fracasarían pero son aceptados por entrar en resonancia con lo que una comunidad científica considera como válido en un momento dado. Otros por el contrario, podrán ser más acertados, pero son rechazados (incluso su publicación) al no cumplir los requisitos anteriores, calificándoseles de disparatados o simplemente de erróneos. ¿Entrarán en esta tesitura los actuales modelos de circulación general de la atmósfera o de la atmósfera-océano? El tiempo dictará sentencia. Pasemos ahora al primer tipo de dificultades comentado.
Abundan os modelos, como por ejemplo los que intentan predecir la erosión o la hidrología de una ladera” cuyo principal obstáculo a sortear resulta ser su universalidad. He visto y leído muchos. Sin embargo, tras años de experiencia puedo decir sin temor a equivocarme que fallan como una “escopeta de ferias”. Generalmente, sus arquitectos comienzan a estudiar un ladera concreta (nunca hay dos iguales), bajo una vegetación o usos del suelo determinados y un clima específico, acumulando datos durante un lapso breve de tiempo (los proyectos de investigación no dan para más). Después intentan detectar las variables que rigen el problema, elaboran matemáticamente una formulación y proponen su producto al público. Obviamente en su lugar de estudio podrán predecir más o menos bien, aunque incluso a menudo ni allí. Luego, en el mejor de los casos, intentan (ellos u otros investigadores) testarlos en otros ambientes y aquí comienza el problema. Lo que en un lugar funciona en otro no. Empero la mayoría de ellos admiten parametrizaciones, es decir ciertas constantes deben calibrarse en el nuevo sitio antes de correr el producto. Resulta que esta última operación también requiere años de recogida de datos, por lo que estos suelen ser insuficientes, so pena que resulte más viable hacer otro modelo nuevo, lo cual a veces es más económico. Me explico, para los casos de la erosión y la hidrología de laderas, dada la enorme variabilidad climática de muchos ambientes, como lo es el mediterráneo, se necesitan muchos años con vistas a obtener un cuadro sinóptico aceptable. Pero en muchas disciplinas se presentan problemas similares o equivalentes. Lo mismo ocurre con las funciones de edafotransferencia y los índices de calidad del suelo (que no dejan de ser modelos, aunque muy simples), que tan solo son válidas a nivel local. Sin embargo se persevera en buscar el Santo Grial: su universalidad.
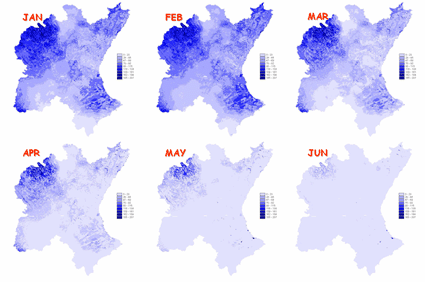
Humedad del suelo en la Cuenca del rió Jucar
Salida de un modelo de simulación
En otras ocasiones, como es el caso de la USLE (Ecuación Universal de perdida de suelos), se sabe desde hace tiempo que no funcionan y también las razones. Sin embargo, debido a que los gestores medioambientales derrochan enormes cantidades de dinero para ofrecer al público (de poco más sirven) mapas de riesgos erosivos, y hablar después sin conocimiento de causa de las toneladas de suelo que perdemos, etc., etc., sigue aplicándose con preocupante asiduidad Me comentaba un día Carlos Roquero (antiguo Catedrático de edafología de la ETSI Agrónomos de la UPM) que uno de los padres de la USLE se lamentaba que su fracaso era debido a que no se aplicaba correctamente. Don Carlos acertadamente le respondió que la culpa era suya por haberla etiquetado cono “Universal”, cuando había sido testado en estaciones experimentales de EE.UU., bajo condiciones muy concretas: suelos profundos, escasa pendiente, sin pedregosidad, etc.
No existe un único proceso erosivo, sino múltiples, y cada uno regido por variables diferentes. Sin embargo, lo que se le pide a los investigadores es una estima global, lo cual es imposible. Pero de algún sitio hay que sacar dinero. En consecuencia, muchos expertos aplican la USLE y “a tomar vientos”. Eso sí, la mayoría de ellos saben sobradamente que es dinero malgastado. Otro producto basura en el marcado. En otras palabras, se sigue trabajando a sabiendas de que la USLE ni es universal ni funciona.
Del mismo modo, los modelizadores intentan demostrar desesperadamente que su modelo funciona, realizando cualquier maniobra “ad hoc” para conseguirlo. Permitirme que os comente una historia que me narró mi amigo Juan Sánchez, Catedrático de la UV y exdirector del CIDE. En un macroproyecto europeo sobre cambio climático, unos participantes holandeses habían desarrollado un modelo hidrológico. Este debía ser testado en una de las zonas de estudio, que resultó ser la tierra de Don Quijote (La Mancha). Pues bien, cuando fueron a validarlo se toparon con que había “horizontes petrocálcicos o calicretas”, es decir capas del suelo subsuperficiales que pueden llegar a estar tan endurecidas como una roca. Sin embargo bajo ellas generalmente se sigue extendiendo suelo deleznable. Como no habían considerado tal eventualidad (es decir, no se habían preocupado por profundizar en conocer las características edáficas de la zona de estudio) aquello no funcionaba. Enojados, recogieron sus enseres y se fueron a Chipre a probar suerte (creo recordar que por allí también abundan este tipo de horizontes). Dicho de otro modo: “si la naturaleza no se acomoda al modelo, busquemos en donde esto ocurra con vistas a demostrar sus bondades.
Pues a lo que vemos: ¿Podemos decir que en todos estos casos (y en otros muchos) los modelizadores cumplen con los cánones de la ciencia? Sinceramente pienso que no. Si un modelo falla, o si no es corroborable-refutable en un plazo razonable de tiempo, no puede considerase un producto científico en el sentido estricto del término. Sin embargo la literatura científica contemporánea se encuentra repleta de publicaciones de esta guisa. Lamentablemente resulta más difícil publicar trabajo con datos de campo que proponer un modelo, y cuanto más elegante y complejo (personalmente considero que se trata de dos conceptos que se pegan de patadas) mejor. ¿Y funcionará? Eso que lo hagan otros. Nosotros ya hemos cumplido, también lo he escuchado.
No he encontrado libros de filosofía de la ciencia (pero puede haberlos) que hablen del dudoso status epistemológico de los modelos numéricos de simulación predictivos. Personalmente considero que en muchos casos son necesarios pero: (i) no hay que confundir predicciones con la realidad (por ejemplo no disponemos de datos fiables sobre pérdida de suelo por erosión a escalas geográficas amplias) y (ii) hay que poner coto y orden a tanta publicación sobre nuevos modelos, muchos de los cuales no son corroborables ni refutables en la práctica so pena de gastarse enormes cantidades de dinero y tiempo para testar cada uno de ellos y mostrar su validez, universalidad o “rango geográfico de pertinencia”. Nos faltan datos de campo, no modelos a la hora de realizar muchos estudios. Esta sí que es la pura realidad. Finalmente mentar que, obviamente existen modelizaciones numéricas que sí cumplen con los cánones científicos, por supuesto. Obviamente otras no.
Rhené Thom, padre de la Teoría de Catástrofes, tras ver como se creaba un centro de aplicaciones de su criatura en UK, en el que se intentaban predecir con ella los más disparatados temas, espantado, decidió enterrarla. A la postre, fue de facto uno de los principales responsables de su olvido, cuando “aparentemente” tenía un futuro mucho más prometedor. Vamos que hizo lo que Popper habría aplaudido con entusiasmo.
La naturaleza es muy compleja, nuestros conocimientos precarios y los modelos muy simples
Pero que más da que fallen o no: para cuando no se pueden corroborar (….)
Juan José Ibáñez
Sumario de los post editados en “Curso Básico sobre Filosofía y Sociología de la Ciencia hasta este post (pinchar en los números para desplegar los post)
¿Qué es esa cosa llamada Ciencia?
Curso Básico sobre Filosofía y Sociología de la Ciencia
Ciencia e Inducción [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13,]
El Círculo de Viena y el Positivismo Lógico [41]
Filosofía de Karl Poper: El Falsacionismo [14, 15, 16, 19, 20, 21, 23, 24, 25, 26]
Filosofía de la Teoría de la Evolución y Sociedad [17, 18],
Naturaleza y enseñanza de la Ciencia [22]
Las Teorías Científicas Como Estructuras Complejas
La Filosofía de Imre Lakatos [28, 29, 30, 31, 32]
La Filosofía de Thomás Kuhn [33, 34, 35, 36, 37]
Filosofías Radicales de la Ciencia: Feyerabend y más [38]
Filosofía de la Ciencia versus filosofías científicas [39]
¿Es la mente fractal? [40]
¿Filosofía Cuántica? [42]
Seredipidad o Serendipia y la Lógica de los Descubrimientos Científicos [43]
El Dudoso Estatus de los Ciencia Modelos de Simulación Predicativos [43]

Más sobre esto, visto desde diferentes perspectivas en:
http://golemp.blogspot.com/2007/01/modelos-realidad-incertidumbre-y-turing.html
http://malaciencia.blogspot.com/2006/12/simulaciones-y-modelos-informticos.html
http://curiosoperoinutil.com/2006/12/15/el-efecto-mariposa/
Una buena referencia sobre la reciente discusión de los modelos y las simulaciones en la filosofía de la ciencia
http://www.tilburguniversity.nl/faculties/humanities/tilps/MS2/
Hola,
Hace un tiempo inicié un blog, llamado TemaTerra [1] en el que me propongo tratar temas de hidrología, clima y meteorología. Precisamente, he querido empezar tratando el tema de la modelización por la simple razón que creo, en esto estamos de acuerdo, que se abusa de ellos (yo trabajo en modelización).
Te dejo el enlace a los apuntes (tengo previsto publicar uno sobre hidrología en los próximos días), creo que te pueden interesar.
http://blog.tematerra.info/search/label/modelos»>http://blog.tematerra.info/search/label/modelos
Me ha gustado mucho leer el mismo tema desde el punto de vista de la edafología.
Te seguiré leyendo.
[1]: http://blog.tematerra.info
Angel, Jesus y PQS muechas gracias por la información y esyoy ya leyendo parte de los contenidos que citáis.
Cordiales saludos
Juanjo Ibáñez
no encuentro que es ecuacion aqui sale pero en matematica y yo la quiero de biologia