Las Leyes Fractales de los Procesos Superficiales terrestres (Terremotos, Deslizamientos, Avalanchas, Aludes, Lluvias Torrenciales, Inundaciones, etc.)

Como comentábamos el otro día en el post sobre terremotos y procesos superficiales terrestres, tanto la magnitud- frecuencia de terremotos (sismos), deslizamientos, avalanchas y aludes siguen leyes de escala, es decir se ajustan a distribuciones potenciales. Resulta sumamente interesante que todos estos eventos catastróficos se comporten de la misma forma. Recordemos que las estructuras fractales son huellas de lo que denominamos sistemas complejos o no lineales. Básicamente, podemos decir que el número de acontecimientos de escasa magnitud son muy numerosos y decrecen rápidamente conforme aumenta aquella. En otras palabras los terremotos, deslizamientos, avalanchas, aludes, lluvias torrenciales, inundaciones, etc.,  de escasa magnitud son muy abundantes, mientras los que llegan a generar verdaderas catástrofes muy raros o poco numerosos. ¡Menos mal!, ¿Verdad? Lo realmente intrigante es que los procesos superficiales terrestres y los que acaecen en el interior de la tierra (aunque se manifiesten en superficie) sigan el mismo comportamiento aunque sean producto de causas muy diferentes. Veamos cual es la razón.

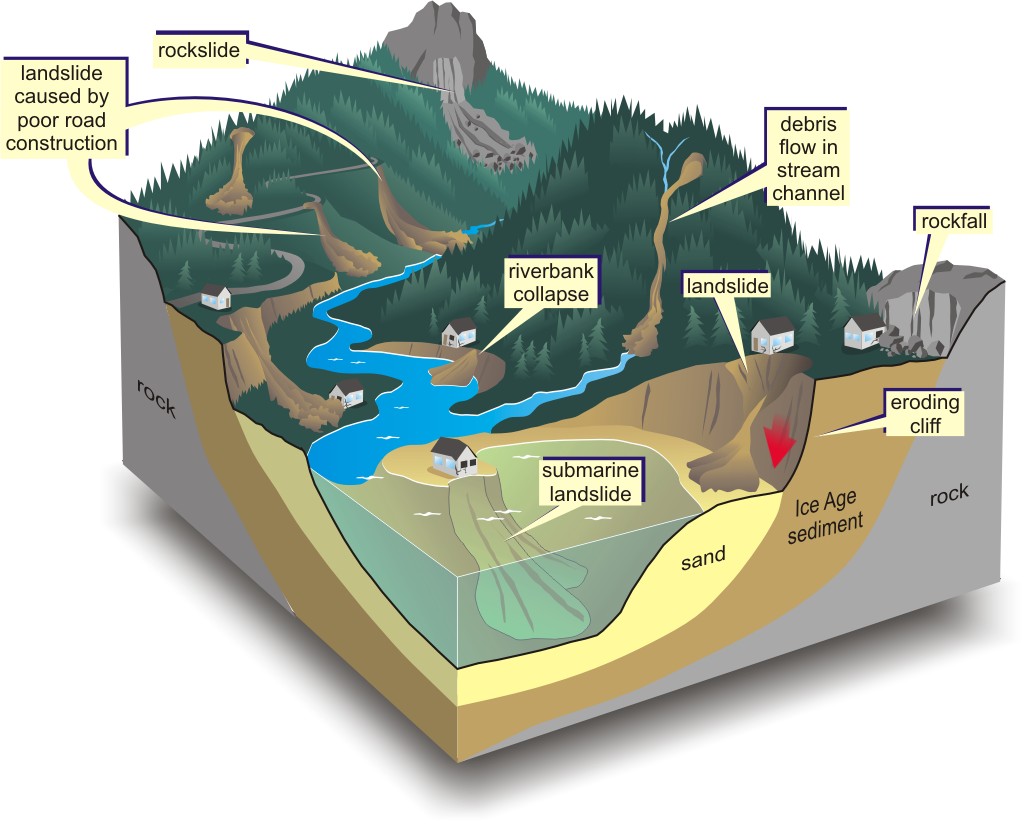
Tipos de Deslizamientos, aludes

y avalanchas Fuente: aquí

Ya hemos hablado en numerosas ocasiones de las leyes de escala, distribuciones potenciales y fractales. Todos esos post están incluidos en las categorías sobre diversidad y taxonomía. Recordemos de una forma sencilla como puede detectarse una ley potencial. Si disponemos en coordenadas cartesianas el logaritmo del número de eventos (en un eje) respecto al logaritmo de su magnitud (el otro eje) los datos se ajustan a una línea recta. En una distribución lineal obtendríamos la misma estructura sin tales trasformaciones logarítmicas. Del mismo modo, sin las mentadas transformaciones una distribución potencial daría lugar a una curva que crece hacia primero rápidamente, para decaer después hacia una asíntota que jamás termina de alcanzar. Por tanto una ley potencial nos predice por ejemplo, que el número de eventos de una determinada magnitud es igual a una constante por la magnitud del evento elevada a un exponente, siendo este último la pendiente de la recta en su representación logarítmica. El exponente está relacionado (e incluso puede ser identificado) con la dimensión fractal de la estructura estudiada.  Obviamente, la constante y el exponente no son los mismos para cada uno de los eventos descritos.

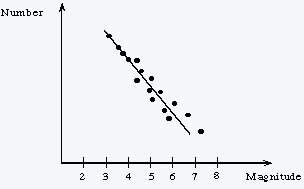
Ley Potencial para la magnitud frecuencia de terremotos

Lo realmente fascinante e incluso intrigante, resulta ser, que procesos tan dispares, inducidos por mecanismos tan diferentes obedezcan a las mismas leyes, tanto en la superficie terrestre (geodinámica externa), como en el motor de la tectónica de placas (geodinámica interna).

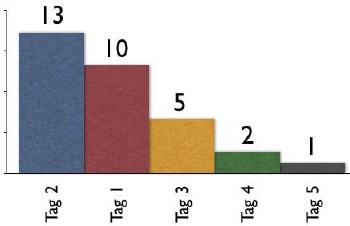
Estructura numérica de una ley potencial en las folksonomías

de internet: los grandes números corresponderían al número

de eventos de escasa magnitud y los pequeños a los grandes

Fuente: Wanderwal Net

Sin embargo, tales similitudes pueden dar lugar a interpretaciones erróneas. Por ejemplo, pudiera pensarse que la magnitud-frecuencia de las avalanchas aludes y deslizamientos causados por terremotos obedecen a leyes potenciales por ser la consecuencia de la magnitud-frecuencia de los terremotos (lo mismo podría decirse de los causados por lluvias torrenciales extremas). Sin embargo no es necesariamente así. Ya explicaremos en otro post, cuando hablemos de la física de los fractales (criticalidad autoorganizada) y los tipos de perturbaciones aludidos, como cada uno de ellos se ajusta a los mismos patrones independientemente. Por ejemplo si observamos un reloj de arena, se puede demostrar que conforme caen los granos sobre la pila inferior, en esta se producen muchos deslizamientos pequeños y muy pocos grandes, ajustándose también experimentalmente a una ley potencial. Empero lo que no cabe duda es que al acoplarse una proceso-causa (por ejemplo un terremoto) que se distribuye a una ley potencial, con un proceso efecto (por ejemplo los movimientos de suelo producidos pos aquel) que sigue el mismo patrón, algún tipo de “digamos” resonancia debe ocurrir. Sin embargo no he logrado encontrar aun bibliografía a este respecto.

Gráfico de una Ley Potencial.

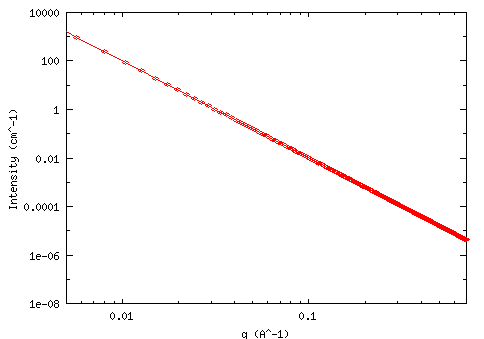
Nótese como en los dos ejes los datos

Han sido transformados logarítmicamente

Desafortunadamente tal comportamiento fractal no nos ayuda a detectar o predecir cuando un evento catastrófico va a suceder. Sin embargo, no todo es negativo. ¿Qué ocurriría si tales eventos fueran conforme a leyes exponenciales, que no potenciales? Pues resulta, como veremos en el siguiente post sobre el tema, que la situación sería mucho peor.

Digamos para finalizar, que en este post hemos hablado de procesos pero ¿Qué ocurre con las estructuras espaciales de la superficie terrestre? (como distribución de masas de tierra emergida en función de su extensión, frecuencia-dimensiones superficiales de las cuencas de drenaje y un largo  etc.). Como veremos en otros post, más de lo mismo. Desconcertante y fascinante ¿no?

Juan José Ibáñez