![]()
Concepto de Complejidad
Con independencia del valor intrínseco de los estudios de diversidad, cada vez son más evidentes las relaciones existentes entre los patrones detectados mediante las herramientas matemáticas que pretenden dar cuenta de ella, con otros descritos acudiendo al auxilio de los recientes avances en las denominadas ciencias de la complejidad (sistemas no-lineales o al borde del caos, fractales, etc.) Pero, ¿que es la Complejidad? ¿Cómo podemos definirla? En este post lo vamos a intentar desde un punto de vista un tanto singular. La idea se me ocurrió para un artículo, que junto a Asunción Saldaña, publicamos el año 2007 en “Ecological Modelling”. Para ello partiremos de tres conceptos centrales y dos, a los que denominaremos conectores. Todos los elementos necesarios están en el gráfico de abajo. Veremos que el concepto que presentamos es sumamente sencillo. No recurriremos a ningún formalismo matemático. No pretendemos en este post analizar las propiedades de los sistemas no lineales, sino de cómo entender la estructura de lo que hoy se entiende por sistema complejo. Os lo prometimos en este post, y seguiremos avanzando en otros que le sigan, con vistas a mostraros la ubicuidad de ciertas estructuras a nuestro alrededor, desde el mundo inanimado, pasando por los seres vivos, artefactos tecnológicos, hasta el propio crecimiento de la Web. Como cualquier concepto sencillo, omite una buena parte de la esencia del tipo de sistemas mentados. Sin embargo, considero que puede ser un buen comienzo.
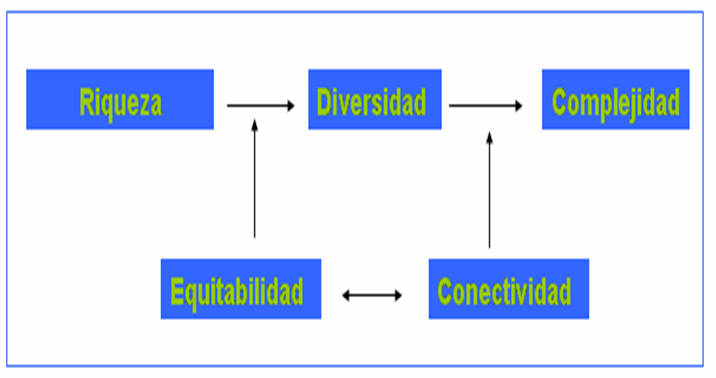
Esquema conceptual de cómo entender un sistema complejo
Fuente: Elaborado y reelaborado por J.J. Ibáñez y Asunción Saldaña
Consideremos un sistema que esta compuesto por una serie de elementos pertenecientes a diferentes clases o categorías. Para los que estéis familiarizados con los estudios de biodiversidad o edafodiversidad, digamos que se trataría de una comunidad (biocenosis) o de un edafopaisaje (ensamblaje de suelos). En cualquier caso vale para cualquier tipo de sistemas.
El numero de clases (por ejemplo especies biológicas o edafotaxa) distintas es denominado “riqueza” (“S”) (primer concepto central). Sin embargo, es obvio que con tal magnitud el sistema queda pobremente definido, digamos que de un modo muy cualitativo. No todas las clases atesoran el mismo número de individuos, teniendo unas más que otras. Pensemos pues en la población de individuos que conforman el sistema como un conjunto. Cuando tenemos en cuenta como los individuos se distribuyen entre las diferentes clases, obtenemos lo que se llama “diversidad” (“H’”) (segundo concepto central). Tanto la termodinámica, como la teoría de la información, nos informan que la mayor diversidad se alcanza cuando cada clase posee el mismo número de individuos. ¿Por qué? Resulta trivial que si un sistema atesora 1000 individuos pertenecientes a cinco clases distintas y uno de ellos acumula 996, mientas los otros cuatro uno cada uno, el sistema será menos diverso que otro en el que se repartan equiprobablemente (200/25). La estimación de la asimetría-simetría acerca de cómo se distribuyen los individuos entre las clases se estima mediante lo que denominamos “equitabilidad” (“E”) (primer concepto conector). La distribución menos equitativa sería la que corresponde al primer ejemplo (E = 0), y la más equitativa la que da cuenta del último (E = 1), entre todo el espectro de posibilidades distintas para un sistema con 1000 individuos y 5 clases. Por lo tanto, la diversidad (segundo concepto central) se alcanza al aplicar el primer concepto conector al primer concepto central. Para un sistema cualquiera, la equitabilidad puede ser cuantificada al dividir la distribución observada de los individuos entre las clases por la máxima posible. Obtenemos así un índice, que como ya esbozamos arriba, fluctuaría entre 0 y 1.
Ahora bien, inmediatamente nos damos cuenta que, si bien el sistema esta mejor caracterizado, aun padece de una carencia esencial. En todos los sistemas las clases interactúan entre sí de alguna manera, y la diversidad no nos dice nada acerca de ello. Tales interacciones pueden representarse mediante flechas que unen las clases, a las que llamaremos nodos. Visto de esta manera, obtenemos un grafo del sistema cuando se representan los nodos y las flechas, como ocurre en la figura de abajo.
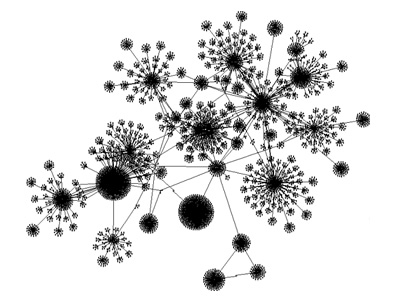
Ejemplo del grafo de un sistema cualquiera
Observar que la racionalidad subyacente a ambos conceptos conectores es idéntica. Tanto la equitabilidad como la conectividad se cuantifican midiendo lo observado por la máxima posible. Se trata pues de razones, en el sentido matemático del término. Para el caso de la riqueza, equitabilidad y diversidad, ya esbozamos en este post las matemáticas subyacentes. En otros muchos post incluidos en la carpeta “Diversidad, Complejidad y Fractales” podréis encontrar abundante información adicional sobre estos temas.
¿A que el modelo es sumamente sencillo e intuitivo? Obviamente en la práctica surgen numerosos problemas a la hora de definir las clases, enumerar el número de individuos y averiguar como interactúan entre sí (no siempre con la misma intensidad y de una manera biunívoca). Se trata de la representación conceptual más sencilla que he visto sobre el tema, o al menos a mi me lo parece. Claro está, que la he elaborado personalmente en colaboración con A. Saldaña (UAH), y eso puede inducir a que me parezca muy elemental, aunque pudiera no serla. Debe quedar claro que no estoy alegando haber realizado innovación alguna en el tema aquí tratado. Simplemente recogí conceptos y magnitudes muy aceptados en la bibliografía y los engarcé en el modelo conceptual más sencillo que me fue posible. Tan solo he pretendido que entendáis como se puede llegar al “concepto de complejidad” de una manera más simple posible. Reitero que en la práctica surgen problemas muy serios, se han propuesto numerosos índices, etc., etc. Pero, ¿Existen regularidades en los patrones de riqueza, diversidad, equitabilidad, conectividad y complejidad, en los sistemas no-lineales? Por supuesto que sí. Ya los iremos viendo.
Juan José Ibáñez
Continuará….

algunas de estas ideas pueden conectarse, si se quiere y desea, con algunas de las que están recogidas en el siguiente artículo, que ya tiene 15 años de vida:
http://arxiv.org/abs/nlin/0205033
"Llueve sobre mojado", espero que tal denominación no implique que he plagiado algo. No es así. He mirado el paper y efectivamente como versa sobre el tema. Yo también he hecho cosas. La cuestión es que utilizamos formulas mucho más complejas y no son aptas para explicar de una forma sencilla el concepto al ciudadano.
En cualquier caso gracias por la información. En mis primeros post y en la galería de diversidad hay formas más sofisticadas para estimar la compejidad pero en el contexto de este post no proceden
Saludos
Juanjo Ibáñez
dios me libre de tal sugerencia.
simplemente decir que todos andais dando vuelta a lo mismo pero en distintos lenguajes, incluido ese paper ahi linkado y que en su campo ha sido bastante citado.
y de paso aprovecho para felicitarte por tu blog, que es magnifico.
Si tienes razón. El problema estriba en que no hay aun una fórmula correcta y sencilla para medir la complejidad, como ocurre con la diversidad. Las del mercado cuando tienen unas decenas de clases son inviables por el gasto de cómputo. Medir mejor la conectividad es también otro dilema ya que las interacciones no incluyen las intensidades y que entre dos elementos pueden ser distintas en una dirección que en la otra. Y aquí se ha topado con una pared que se debe romper.
Cordiales saludos. Reitero que era para los que no supieran que es la complejidad de un sistema ya que paralos que saben…..
Juanjo Ibáñez
Gracias por tu valoración del blog: siemplemente se hace lo que se puede.
[…] milagrosas” para determinar el grado de complejidad, hecho que ya explique al hacer frente al “Concepto de Complejidad”. Pues bien, antes de entrar en más detalles que atañen a la evolución biológica, social, […]
[…] Concepto de Complejidad […]