Cartografías a diferentes escalas, autosimilares y anidadas (Fractales y Mundos Pequeños)

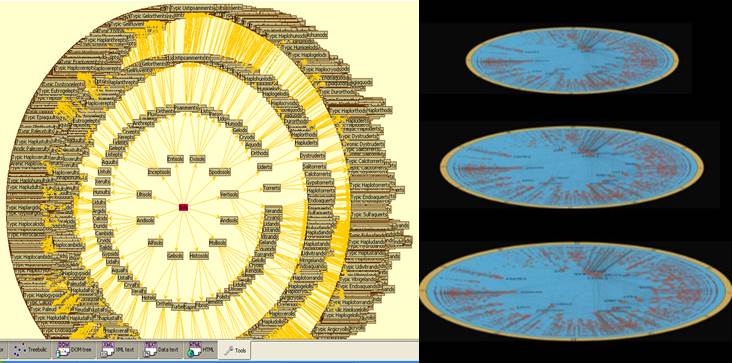
Representaciones cartográficas anidadas hiperbólicas según Juan José Ibáñez para taxonomías de suelos y de la nota de prensa analizada para análisis de redes.

La iniciativa de crear mapas autosimilares anidados a diferentes escalas, se nos antoja de lo más interesante, por cuanto ayudaría a generar bases de datos georreferenciadas anidadas de cada recurso natural (o combinación de algunos de ellos) en donde se contenga su información de una forma más manipulable y eficiente, siendo fácilmente actualizables y no sometidas a la perdida de los detalles/diversidad que surgen en el proceso de generalización cartográfica.

Cuando los autores del estudio que mostramos hoy hablan de; “redes complejas con características similares (…) a diferentes escalas”, sencillamente nos informan de “estructuras fractales”. Y más adelante al hablar de redes mentan: “(…) sistemas son redes multiescalares, es decir, su estructura, o los procesos asociados, son el resultado de mezclas de estructuras y de procesos a escalas diferentes”. Seguidamente continúan afirmando que: estos sistemas se pueden definir como redes complejas porque tienen la propiedad conocida con el nombre de ‘mundo pequeño’, es decir, muchos nodos están conectados entre sí mediante unos pocos pasos. Ya os comentamos que son los mundos pequeños en post precedentes, como también de sus características, relacionadas con lo que hemos venido a denominar “curvas de Willis”, que dan cuenta de las características elementales de sus estructuras. Y por lo tanto: Esta técnica “permite explorar un sistema a diferentes resoluciones espaciales, como una especie de microscopio inverso que nos posibilita hacer un zoom hacia fuera y aumentar la escala a la que lo observamos”.

Dos cuestiones se nos antojan de sumo interés. En primer lugar aunque los autores del estudio, en la nota de prensa, nos informan de que las técnicas de re-normalización que ellos usan fueron desarrolladas para otros fines: ¿Qué nos impide que también sean aplicadas para la representación de información cartográfica? Francamente no veo ninguna aunque hubiera que realizar algunas modificaciones en sus procedimientos matemáticos e informáticos, lo cual desconozco.

¿Se trata de una novedad?. Desde un punto de vista informático sí. Ahora bien, como describimos en post precedentes (almacenados en la categorías: ‘Redes Complejas, Ecológicas, Sociales y el Mundo de Internet’), los cartógrafos de suelos, y posiblemente de otros recursos, tienden a llevar a cabo tales menesteres mediante unos estándares que, “curiosamente”, fueron aceptados por la comunidad científica, sin percatarse de que, al hacerlo, se encontraban ya generando una manera de llevar a cabo planes nacionales de mapeo a diferentes escalas de una forma similar a la que los investigadores pretenden automatizar ahora. Y por ello, hablamos de la “mente fractal” “de los cartógrafos” en otros posts. Pero aquí no paran las coincidencias entre lo que se venía haciendo intuitivamente y lo que ahora se nos muestra como una forma racional y eficiente y estudiar la información espacial de un sistema.

También vimos que las taxonomías de suelos, en general, atesoran unas estructuras que tienden a ser fractales, aunque por ciertos sesgos humanos (cognitivos y de otra índole) terminan siendo multifractales. También os explicamos que las clasificaciones de suelos no dejan de ser redes que por su estructura, atesoran unas propiedades muy concretas y que dan lugar a que podamos considerarlas al menos semejantes a los denominados mundos pequeños, que los investigadores del estudio que analizamos hoy explican en la nota que os reproducimos al final del post.

Como sabéis, en una taxonomía jerárquica, las categorías superiores son agrupaciones o “clusters” de los taxones del rango inmediatamente inferior. Del mismo modo, los estándares cartográficos proponen el uso de leyendas en las cuales cada escala, desde la más detallada a la más grosera, se vinculan con las categorías taxonómicas de rango ascendente, por ejemplo, de series a familias, de estas a subgrupos, grandes grupos, subórdenes y finalmente órdenes, si seguimos la nomenclatura de la USDA ST.

Resulta un tanto sorprendente que este tipo de estructuras que utilizamos en edafología clásica emulen: “Es la primera vez que se ha definido un grupo de renormalización verdaderamente geométrico en redes complejas”. ¿Resulta ser la primera vez?. Pues va a ser que en líneas generales no, aunque fuera de una forma más prosaica”. Lo que parece ocurrir deviene en que los autores de la investigación han logrado racionalizar, demostrar, modelizar y operacionalizar matemáticamente, lo que de forma más intuitiva se lleva a cabo en las representaciones cartográficas y taxonómicas tradicionales. Se trata pues de un estudio muy interesante.

Llevo años investigando en este tema, aunque de forma empírica, las relaciones entre la “realidad de campo”, representaciones cartográficas y taxonomías de suelos, habiendo llegado a conclusiones similares. Resumiendo, aunque no atendemos a estos asuntos, las taxonomías y mapas de los recursos naturales tienen a adoptar estructuras eficientes, debido a que nuestros sistemas cognitivos llevan a cabo tal ordenación de la información “inconscientemente”.

Finalmente, merece la pena mentar, que esos mapitas de la figura, en principio, un tanto extraños, resultan ser lo que se denominan representaciones hiperbólicas, y que nosotros sugerimos ya en 2008, como un sistema muy eficiente de manejar/usar las taxonomías de suelos que es posible y recomendable, con las tecnologías actuales de computación, siendo bastante sencillos de elaborar.

Atando cabos vemos que lo que parece tan especial no lo es cuando llevamos a cabo un metaanálisis de la información.

Juan José Ibáñez

Continua………

Cómo crear mapas ‘cartográficos’ de sistemas reales a diferentes escalas

¿Qué tienen en común internet, la red mundial de aeropuertos, el proteoma humano, la música, El origen de las especies de Darwin, el sistema de correo de una empresa, la red metabólica celular humana y el cerebro de una mosca? Todos son redes complejas con características similares.

Un equipo del Instituto de Sistemas Complejos de la Universidad de Barcelona (UBICS) formado por Mª Ángeles Serrano, Guillermo García Pérez y Marián Boguñá han aplicado a redes reales, como internet o el cerebro, la técnica que en física estadística se conoce como renormalización geométrica. Los detalles los publican en la revista Nature Physics.

«Esta técnica permite explorar un sistema a diferentes resoluciones espaciales, como una especie de microscopio inverso que nos posibilita hacer un zoom hacia fuera y aumentar la escala a la que lo observamos», apunta Serrano, directora del trabajo y profesora de investigación ICREA.

«El hecho de poder moverte por una red a diversas escalas es muy relevante en sistemas en los que tienes muchos elementos que interaccionan, como las redes que hemos estudiado. Estos sistemas son redes multiescalares, es decir, su estructura, o los procesos asociados, son el resultado de mezclas de estructuras y de procesos a escalas diferentes», explica García Pérez, primer autor del trabajo. «Cada escala contiene información específica, pero, por otra parte, las escalas están interrelacionadas entre sí«.

Los investigadores han aplicado la técnica a multitud de sistemas: internet, la red mundial de aeropuertos, el proteoma humano, la música, El origen de las especies de Darwin, el sistema de correo de una empresa, la red metabólica celular humana y el cerebro de la mosca Drosophila.

Aunque aparentemente son muy distintos, todos ellos se pueden definir en forma de nodos y conexiones. En algunos casos, como el de internet, conocemos bien cuáles son; en otros, como en el de la música, los investigadores han considerado los acordes como nodos y las conexiones como la proximidad de dichos acordes en canciones de música moderna.

LA PROPIEDAD DEL ‘MUNDO PEQUEÑO’

En cualquier caso, todos estos sistemas se pueden definir como redes complejas porque tienen la propiedad conocida con el nombre de ‘mundo pequeño’, es decir, los nodos están conectados entre sí mediante pocos pasos.

«Precisamente debido a esta propiedad de mundo pequeño, hasta ahora había sido imposible separar estas escalas estructurales en redes complejas reales y, para hacerlo, primero hemos tenido que desarrollar los mapas geométricos de cada una de ellas con el fin de poder definir distancias entre nodos«, explica el profesor Boguñá.

La técnica se ha aplicado a multitud de sistemas: internet, la red mundial de aeropuertos, el proteoma humano, la música, un libro, la red metabólica celular, el cerebro de una mosca…

Por otra parte, estas redes cumplen dos propiedades más: por un lado, tienen una conectividad heterogénea, es decir, que hay elementos con mucha conectividad y otros con poca; y, por otro, presentan muchas agrupaciones de nodos en forma de triángulo (clusterización).

«Es la primera vez que se ha definido un grupo de renormalización verdaderamente geométrico en redes complejas«, apunta Serrano, quien añade: «Ahora podemos construir mapas de redes complejas en el sentido más cartográfico de la palabra, verdaderos mapas en que los elementos o nodos de las redes tienen unas posiciones y unas distancias entre ellos. Estos mapas no son solo representaciones visuales atractivas, sino que están cargados de significado y permiten descubrir mucha información sobre los sistemas y navegar por ellos«.

En ese sentido, «podemos incrementar la navegabilidad de los sistemas si tenemos en cuenta la información que nos da el grupo de renormalización», que permite desplegar las redes en las distintas escalas estructurales que las componen, que además resultan ser autosimilares entre ellas, es decir, que tienen la misma organización a diferentes escalas.

Este resultado también se puede aplicar para hacer versiones reducidas de las redes originales a escala más pequeña y que tienen exactamente las mismas propiedades. «Esta posibilidad de hacer réplicas reducidas tiene un gran potencial; por ejemplo, se pueden utilizar como banco de pruebas para evaluar procesos computacionalmente muy costosos en las redes originales, como nuevos protocolos de enrutamiento de información en Internet», concluye Serrano.

Referencia bibliográfica:

G. García-Pérez, M. Boguñá y M. Á. Serrano. 2018. Multiscale unfolding of real complex networks by geometric renormalization. Nature Physics. DOI: 10.1038/s41567-018-0072-5

Algunos post Previos sobre Taxonomías y Clasificaciones de Suelos

Levantamentos Pedológicos Detalhados No Brasil (Foro de discusión em Português & Español)

Los Números Mágicos de las Taxonomías y Ciencias Cognitivas: A Meta-Analysis for Enlarging the Scope of a Universal Soil Classification System is coming soon

Categorización, Clasificación y Partición: El Caso de las Taxonomías de Suelos

Clasificando los Suelos Desde la Edafosfera a los Edafotaxa: La Categorización

¿Porqué las Clasificaciones de Suelos Suelen Ser Jerárquicas?

Los Rasgos Matemáticos Elementales de las Clasificaciones de Suelos (y Biológicas): Las Curvas de Willis

Los Sesgos Geográficos de las Taxonomías de Suelos (y las Biológicas)

Las Taxonomías como Sistemas de Información y el Criterio de Ernest Mayr

Taxonomías Edafológicas y Biológicas: Teoría de la Información y Entropía

Taxonomía de Suelos y Sesgos Cognitivos: El Efecto Prototípico de Rosch

Paradojas Taxonómicas: ¿Qué es la Paradoja de Gregg?