![]()
Mikhail Grómov, Premio Abel 2009
El pasado 26 de marzo, la Academia Noruega de las Ciencias y las Letras anunció que se había decidido ortorgar el Premio Abel para el año 2009 a Mikhaíl Leonídovich Grómov, por “sus contribuciones revolucionarias en la geometría”. El Premio Abel es considerado como el análogo al premio Nobel para las matemáticas. Fue establecido en 2002 por el Niels Henrik Abel Memorial Fund, y se otorga anualmente desde 2003. La selección del premiado se basa en la recomendación de una Comisión formada por cinco matemáticos de reconocido presitigio internacional. El premio lleva asociado un premio en metálico de 6 millones de coronas noruegas, equivalentes a 700,000 euros. Mikhail Grómov recibirá el Premio Abel de manos de Su Majestad el Rey Harald de Noruega en la ceremonia oficial del 19 de Mayo en Oslo (Noruega).

Mikhail Grómov es un matemático ruso-francés, conocido por importantes contribuciones en muy diversas áreas de las matemáticas. Nació el 23 de diciembre de 1943, en una pequeña ciudad llamada Boksitogorsk, cercana a Leningrado (ahora San Petersburgo), en Rusia. Cursó sus estudios universitarios en la Universidad de Leningrado y realizó sus estudios de doctorado como estudiante del eminente topólogo Vladimir A. Rokhlin, obteniendo el título de doctor en 1969 y completando sus tesis post-doctoral en 1973. En 1974, Grómov dejó la Unión Sovietica y se convirtió en Profesor de la Universidad de Stony Brook (Nueva York, US). Desde 1982, es Profesor permanente en el Institut des Hautes Études Scientifiques (I.H.E.S.), en Bures-sur-Yvette, París (Francia). Gromov adquirió la nacionalidad francesa en 1992.
Mikhail Grómov ha recibido numerosos premios internacionales de reconocido prestigio, tales como el Premio Nemmers, el Premio Balzan, el Premio Oswald Veblen en Geometría, o el Premio János Bolyai, entre muchos otros, aunque no recibió la medalla Fields. También ha sido un conferenciante invitado en varios International Congress of Mathematicians: Niza (1970), Helsinki (1978), Varsovia (1982), y Berkeley (1986).
El trabajo de Grómov ha tenido gran impacto en numerosas áreas de las matemáticas, dentro del álgebra, el análisis, y la geometría. Grómov se considera a sí mismo un geómetra. Las técnicas que emplea (e inventa) para atacar los problemas están formuladas en general en un lenguaje geométrico. Ha introducido ideas realmente originales que han dado lugar a nuevos puntos de vista. Sus ideas suelen ser intuitivamente sencillas, pero hacerlas funcionar ha requerido en muchos casos un verdadero tour de force que le ha obligado a desarrollar técnicas completamente novedosas, algo al alcance de pocos matemáticos. El Comité del Premio Abel ha expresado que “Mikhail Grómov siempre está a la búsqueda de nuevas preguntas y constantemente pensando en nuevas ideas para resolver viejos problemas. Ha producido trabajo profundo y original a lo largo de su carrera y se mantiene remarcablemente creativo. El trabajo de Grómov sigue siendo una fuente de inspiración para muchos descubrimientos matemáticos futuros.”
Revisemos brevemente algunas de las áreas en las que Grómov ha dejado su impronta.
Análisis
Grómov ha introducido el sorprendente concepto del h-principio. En su libro Partial Differential Relations, Grómov estudia las relaciones en derivadas parciales, que son ecuaciones en derivadas parciales sobre una variedad diferenciable, de tipo generalizado (se permiten condiciones del tipo de inecuaciones en vez de igualdades). La idea principal de Grómov consiste en dividir el problema en dos: uno de tipo topológico, en el que se encuentran soluciones no ‘geométricas’ a las relaciones en derivadas parciales (esto es, jets que satisfacen la propiedad pero que no vienen de funciones sobre la variedad), y otro de tipo analítico, que consiste en deformar una de estas soluciones formales a una solución efectiva (denominada holónoma). Cuando este segundo paso se puede hacer, decimos que el h-principio se verifica.
Grómov utilizó la geometría asociada a numerosos problemas que se pueden expresar en términos de relaciones en derivadas parciales (tales como la construcción de inmersiones de una variedad en otra, de inmersiones isométricas de una variedad riemanniana en el espacio euclídeo, o de inmersiones simplécticas de una variedad simpléctica) para demostrar el h-principio, inventando técnicas de gran originalidad. Por ejemplo, esto sirvió para entender y generalizar el fenómeno descubierto por Smale de la eversión de la esfera, el resultado de Oka de la existencia de secciones holomorfas de un fibrado sobre una variedad Stein, o el resultado de Nash de la inmersión isométrica de una variedad riemanniana en un espacio euclídeo.

Álgebra
El trabajo de Grómov en Álgebra se centra en el estudio de grupos discretos finitamente generados. Estos grupos aparecen como grupos de transformaciones en varias situaciones: en teoría de números aparece el grupo modular SL(2,Z) actuando sobre el semiplano superior, también son relevantes los grupos discretos actuando en espacios homogéneos, que producen los llamados espacios geométricos. En general, los grupos discretos finitamente generados aparecen como grupos fundamentales de variedades diferenciables compactas. Grómov estudió los grupos de crecimiento polinomial, resolviendo una conjectura de Milnor de 1968. Demostró que cada grupo de tipo finito y crecimiento polinomial contiene un subgrupo de indice finito que es él mismo un subgrupo de un grupo de Lie nilpotente. El crecimiento de un grupo se expresa a través de su grafo de Cayley, que se construye fijando unos generadores del grupo, colocando los elementos del grupo como vértices, y uniendo dos vértices cuando uno se obtiene del otro multiplicando por un generador. La cuestión básica es que, mirando este grafo desde el infinito, el resultado no depende de los generadores elegidos, y parece un espacio continuo.
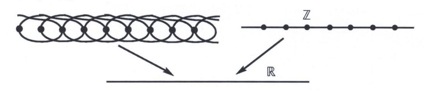
Grupo Z. El primer grafo se corresponde a los generadores {2,3}.
El segundo se corresponde a {1}. Vistos desde el infinito, ambos se convierten en una línea.
El segundo se corresponde a {1}. Vistos desde el infinito, ambos se convierten en una línea.
Para definir el límite al que se aproximaban los espacios al mirarlos desde cada vez más lejos, Grómov introdujo una distancia en el conjunto de todos los espacios métricos completos separables, ahora denominada distancia de Grómov-Hausdorff. Esta noción ha sido usada en numerosas situaciones. Ha tenido especial relevancia en sus aplicaciones a geometría riemanniana, pues formaliza muchas situaciones en las que hay colapsos de espacios.
Otro concepto algebraico de gran impacto introducido por Grómov es el de grupo hiperbólico, en relación con los espacios hiperbólicos, que tienen una gran importancia en geometría.
Geometría Riemanniana
Probablemente el área en el que más repercusión han tenido los trabajos de Grómov es la Geometría Riemanniana. La geometría riemanniana es el estudio de las variedades diferenciales (M,g) dotadas con una métrica g(.,.), es decir, un producto escalar para los vectores del espacio tangente TmM en cada punto. La métrica permite medir longitudes, ángulos y volúmenes, por tanto es uno de los conceptos geométricos que ha tenido más relevancia desde los comienzos de la geometría diferencial. Con la métrica podemos construir los análogos de las líneas rectas en cualquier variedad, que son las curvas que localmente minimizan distancias, y que se denominan geodésicas.
La métrica da una geometría local a la variedad. Esto es, que entornos de puntos distintos en variedades distintas no pueden identificarse con una isometría (una aplicación que preserva las distancias). El invariante local básico de una variedad Riemanniana es el de curvatura. Grómov estudió ampliamente las consecuencias topológicas que se podían extraer de conocer la existencia de una métrica con curvatura prescrita en una variedad compacta. Por ejemplo, demostró que para variedades con curvatura positiva, el número de agujeros de la variedad (la suma de los números de Betti) estaba acotada independientemente de la variedad y la dimensión. Grómov también estudio variedades con curvatura negativa, en relación con los grupos hiperbólicos, así como muchos otros problemas tales como el espectro del laplaciano de una variedad riemanniana, o la distribución de las longitudes de las geodésicas periódicas en una variedad.
Topología Simpléctica
Mikhail Grómov revolucionó el mundo de la geometría simpléctica con la introducción de las curvas pseudo-holomorfas. La geometría simpléctica es el estudio de variedades diferenciables M de dimensión 2n, dotadas de una forma simpléctica, es decir, una forma diferencial ? de grado 2 que es cerrada, d?=0, y no degenerada. Las estructuras simplécticas aparecen en matemáticas en muy diversas situaciones, dos de ellas especialmente importantes. La primera es la geometría Kähler. Una variedad Kähler es una variedad compleja dotada de una métrica hermítica h que oscula con la métrica plana a orden 2. La estructura compleja y la métrica hermítica dan lugar a una 2-forma ? definida como ?(u,v)= Im h(u,v). Los coeficientes de ? en una carta compleja son (salvo un factor) los coeficientes de la métrica h. La no-degeneración de h es equivalente a la no-degeneración de ?. La condición de osculación se traduce por que ? sea cerrada. Por lo tanto, toda variedad Kähler es simpléctica. La segunda situación donde aparece la geometría simpléctica de modo fundamental es la mecánica hamiltoniana, donde la 1-forma canónica del espacio de fases (espacio de posiciones-momentos donde la mecánica se estudia) es la forma de Liouville, y su diferencial exterior es una 2-forma simpléctica.
El teorema de Darboux establece que localmente toda forma simpléctica se puede escribir en algún conjunto de coordenadas (x1, x2, …, x2n) como S dxi ^ dxi+n . Por tanto, no existen invariantes locales en geometría simpléctica, en contraste con la geometría riemanniana, donde la noción de curvatura es el invariante local por excelencia. La topología simpléctica se centra en el estudio de las propiedades globales, o topológicas, de las variedades simplécticas. Sin embargo, Grómov descubrió obstrucciones más allá de la medida en el caso de dimensión 2n = 4. Un resultado paradigmático es la inexistencia de embebimientos simplécticos de una bola B2n(0,R) de radio R (del espacio 2n-dimensional) en un producto B2(0,r) x R2n -2 , con r<R, a pesar que la medida del segundo espacio sea infinita.
La pieza clave para estos resultados de rigidez simpléctica viene de la extensión de la teoría enumerativa de curvas complejas en variedades Kähler a la situación simpléctica. Una estructura casi-compleja en una variedad de dimensión par es un endomorfismo J del espacio tangente cuyo cuadrado es –id, por lo tanto el espacio tangente se convierte en un espacio complejo en el que la multiplicación por i está definida como la acción de J en los vectores. Cada forma simpléctica admite una (de hecho muchas, pero todas ellas deformables entre sí) estructura casi-compleja J compatible.Una curva pseudoholomorfa es una subvariedad real de dimensión 2 cuyos espacios tangentes son subespacios complejos del tangente a la variedad. La clave del trabajo de Grómov estriba en lograr un resultado de estabilidad para la existencia de curvas pseudo-holomorfas cuando variamos J. Uno de los conceptos más conocido es en este campo es el de la compactificación de Grómov del espacio de curvas pseudo-holomorfas, para lo cual se estudian las deformaciones de estas curvas, y como se produce el fenómeno de aparición de burbujas. Asímismo, la teoría de curvas pseudo-holomorfas ha dado lugar a los invariantes de Grómov-Witten y a la cohomología cuántica.
Enlaces
- Marcel Berger, Encounter with a Geometer, Part I, AMS Notices, Volume 47, Number 2
- Marcel Berger, Encounter with a Geometer, Part II, AMS Notices, Volume 47, Number 3
- Premio Abel 2009
Webs
Abel Prize http://www.abelprisen.no/en/
IHES http://www.ihes.fr/jsp/site/Portal.jsp
wikipedia http://es.wikipedia.org/wiki/Mija%C3%ADl_Gr%C3%B3mov
Página personal http://www.ihes.fr/~gromov/
Mathematics Genealogy project
http://genealogy.math.ndsu.nodak.edu/id.php?id=14999
IHES http://www.ihes.fr/jsp/site/Portal.jsp
wikipedia http://es.wikipedia.org/wiki/Mija%C3%ADl_Gr%C3%B3mov
Página personal http://www.ihes.fr/~gromov/
Mathematics Genealogy project
http://genealogy.math.ndsu.nodak.edu/id.php?id=14999
Vicente Muñoz
Investigador Científico
Instituto de Ciencias Matemáticas CSIC-UAM-UC3M-UCM
Investigador Científico
Instituto de Ciencias Matemáticas CSIC-UAM-UC3M-UCM

no silve esta informacion
Gracias por un buen blog. Tu blog es el mejor artículo que leí. Me gusta mucho. Entiendo el artículo fácilmente.