![]()
Invisibilidad Acústica
A continuación recogemos el artículo que Daniel Torrent nos ha enviado explicando los pasos que fueron dando para llegar a este descubrimiento tras su ponencia en la XIII Jornada SIMUMAT: Problemas Inversos, Ondas e Invisibilidad.

La propuesta de Cummer y Schurig tenia una característica que dificultaba seriamente su realización practica, ya que, entre otras propiedades, era necesario que el “manto” estuviera hecho de un material fluido con densidad de masa anisótropa.
Es evidente que este tipo de materiales no existe en la naturaleza, por lo que deben “fabricarse” de forma artificial. Aunque ellos explicaron que un material con densidad de masa anisótropa podía existir, no dieron un modelo analítico que permitiera diseñar dicho material.
Paralelamente mi director de tesis y yo estábamos terminando un artículo en el que, casualmente, demostrábamos que ciertos tipos de estructuras se pueden comportar como materiales con densidad de masa anisótropa y, además, estábamos obteniendo las expresiones analíticas para la densidad de masa (http://www.iop.org/EJ/article/1367-2630/10/2/023004/njp8_2_023004.html).
La propagación del sonido en este tipo de estructuras es compleja y es un campo de estudio muy activo en la actualidad. Sin embargo, cuando la longitud de onda del sonido es grande en relación a la periodicidad de la red, el cristal se comporta como un medio homogéneo. Esto quiere decir que el sonido ya no distingue los centros dispersores como tales, sino que se propaga como si lo hiciera por un fluido homogéneo. Obtener los parámetros efectivos de dicho fluido ha sido el tema central de mi tesis.
Entre otras propiedades, la densidad efectiva de estas estructuras es en general anisótropa, por lo que pensamos que quizá los cristales sónicos eran un buen camino para realizar experimentalmente la invisibilidad acústica.
Como las redes que estábamos estudiando entonces eran redes 2D, estábamos convencidos de que el manto de invisibilidad acústica en dos dimensiones (que era la propuesta original de Cumer y Schurig) podría ser propuesto con este tipo de redes. Sin embargo, estas estructuras presentaban dos características que las hacía incompatibles con el material necesario para lograr la invisibilidad acústica.
En primer lugar, el tensor de masa era un tensor con componentes constantes en coordenadas cartesianas, mientras que la invisibilidad acústica requería un tensor constante en coordenadas polares. Esto quiere decir que nuestras redes tenían una densidad constante si uno se movía en la dirección x o y, mientras que la invisibilidad requería que la densidad fuera constante si uno se movía en la dirección radial o angular. Una forma de resolver esto sería simplemente coger una pieza rectangular de nuestra red y darle forma circular, de modo que lo que antes era la dirección y ahora es la dirección radial, y lo que antes era la dirección x ahora es la dirección angular. Sin embargo esta no fue una buena opción ya que al deformar el material deformábamos también la red periódica y, por lo tanto, las propiedades del medio efectivo también cambiaban. Había que buscar otra solución para “orientar” el tensor.
La otra dificultad que se nos presentaba era, aparentemente, peor todavía. El tensor de densidad que requería el manto de invisibilidad tenía una propiedad muy curiosa: una componente era el recíproco de la otra. Es decir, si en la dirección radial la densidad de masa era, por ejemplo, cien veces la densidad de masa del fluido que contiene el manto (aire o agua), en la dirección perpendicular esta densidad era 1/100, es decir, 0.01 veces la densidad del medio de fondo. Si bien un material con una densidad de masa anisótropa era poco intuitivo, un material con un tensor así nos resultaba realmente difícil de conseguir, ya que nuestras redes presentaban una característica totalmente contradictoria con la que se requería: si la densidad de los cilindros de la red era mayor que la del medio, las componentes del tensor efectivo eran ambas mayores que éste. Y viceversa, si la densidad era menor, las componentes del tensor también lo eran. Parecía que, aunque estábamos en el camino adecuado, éste era largo y más complejo de lo que pensábamos.
La cuestión de la orientación del tensor la resolvimos dando un paso más en la teoría. Tratamos de obtener los parámetros efectivos de redes de “dipolos” (dos cilindros en la celda unidad), en lugar de redes simples. De modo que, para obtener el tensor orientado en la dirección radial y angular, simplemente teníamos que rotar el dipolo. Esta rotación es un cambio mucho menos brusco que la deformación total de la red, y parecía que se mantenían, al menos de forma aproximada, las propiedades del medio efectivo.
Pero esta solución de los dipolos todavía daba un tensor con ambas componentes mayores o menores que la densidad del medio. Esto sucedía porque ambos cilindros en el dipolo eran iguales, ya que la solución de las ecuaciones si los cilindros eran diferentes era muy compleja y no se podía tratar de forma sencilla. Sin embargo, había un caso en el que si que se podía.
Si los dos cilindros del dipolo eran iguales en radio, pero sus densidades relativas a la del medio fluido eran una la recíproca de la otra, las ecuaciones para los parámetros efectivos se podían resolver de forma sencilla y, además, las componentes del tensor efectivo eran una la recíproca de la otra. Por tanto el sistema de dipolos era la solución al problema del tensor de densidad. Cuando ya parecía que el problema estaba resuelto, surgió otro que parecía impedir la realización de la invisibilidad acústica.
Se trataba de una cuestión puramente topológica. Resulta que los parámetros efectivos del manto debían variar radialmente, es decir, a medida que nos acercamos al objeto a ocultar el tensor de densidad debía ser más grande en la dirección radial y más pequeño en la angular, y lo mismo sucedía con la compresibilidad (la otra magnitud acústica definiendo el manto). Esta dependencia radial se puede realizar de forma sencilla: variando el radio de los cilindros para obtener el valor deseado. Es un método que ya habíamos usado en otros trabajos para realizar lentes de gradiente de índice y había funcionado. El problema ahora era que para obtener los valores adecuados de los parámetros efectivos necesitábamos fracciones de llenado más altas de las que los cilindros pueden dar, ya que llega un momento en el que todos los cilindros se están tocando, y entonces quedan huecos por llenar. El valor máximo que de los parámetros efectivos cuando todos los cilindros se estaban tocando era mucho menor del que se necesitaba para conseguir la invisibilidad, por lo que parecía que no lo íbamos a lograr, al menos con este método.
Pensamos en utilizar dipolos de cilindros cuadrados, o formas similares, pero las ecuaciones eran intratables con nuestro método de homogeneización, además de que en ese caso girar el tensor era mucho más difícil. Parecía que nosotros no podíamos llegar más lejos, así que pensamos en escribir un artículo con el tema de los dos cilindros por celda unidad, y seguir probando cosas más adelante. Entonces llegó la solución. Y resultó ser tan sencilla que nos pareció incluso trivial.

Figura 2: Sistema Multicapa de Invisibilidad Acústica.
Es difícil explicar cómo, pero nos dimos cuenta de que los cristales sónicos unidimensionales también tienen una densidad de masa anisótropa. Si construíamos un cilindro mediante capas alternas de un material A y otro B (figura 2), el cilindro efectivo era un cilindro anisótropo con el tensor orientado en coordenadas polares. Además las ecuaciones eran mucho más sencillas y pudimos demostrar que, si la densidad del medio A, relativa al medio de fondo, era la inversa de la densidad del medio B, las componentes del tensor también tenían esa propiedad. Este resultado es un clásico de los sistemas unidimensionales, pero debido a la dificultad de realizar mezclas de distintas capas de fluidos había pasado desapercibido. Sin embargo los cristales sónicos permiten realizar dicha mezcla de fluidos, por lo que pudimos demostrar que el sistema era también realizable1 .
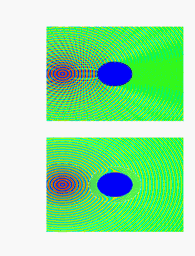
Figura 3: Simulaciones de Dispersión Acústica. Arriba: Cilindro sin «manto» de invisibilidad. Abajo: Cilindro «invisible».
En la figura 3 podemos ver la diferencia que hay entre el campo dispersado por un cilindro cerca de una fuente puntual (arriba) y cómo el cilindro se hace “invisible” cuando lo rodeamos del sistema multicapa de fluidos especialmente diseñado (abajo). Es evidente que la invisibilidad acústica es realizable con materiales isótropos (más fáciles de encontrar en la naturaleza), a pesar de que la propuesta sigue siendo muy teórica. Todavía queda mucho camino por delante para realizar éste dispositivo de forma práctica, pero sin duda alguna es posible.
1 Este trabajo está pendiente de aceptación en New Journal of Physics.
Universidad Politécnica de Valencia
