![]()
Empieza el Workshop «Recent Trends in Algebraic and Geometric Combinatorics» en el ICMAT
El workshop internacional Recent Trends in Algebraic and Geometric Combinatorics se realizará en el ICMAT del 27 al 29 de noviembre, gracias al apoyo del ICMAT, del proyecto de Excelencia en Investigación Severo Ochoa y del proyecto francés del CNRS GDR Renorm. Este encuentro reunirá a unas 40 personas que investigan actualmente en temas dentro de la combinatoria, con el fin de fortalecer la colaboración y fomentar el intercambio de perspectivas en este campo, dentro de Europa. Sus organizadores Kurusch Ebrahimi-Fard (CSIC – España), Vincent Pilaud, (CNRS y LIX, École Polytechnique- Francia) y Juanjo Rué, (Freie Universität y Berlin Mathematical School, Berlin – Alemania) nos presentan esta actividad.
La combinatoria se puede describir como la disciplina de las matemáticas que estudia las estructuras discretas. La magia de este campo es que cada estructura puede (y debe) ser estudiada desde varias perspectivas para obtener un punto de vista global. Por ejemplo, objetos tan elementales como las permutaciones de un conjunto finito o las triangulaciones de un polígono motivan una gran variedad de preguntas combinatorias: su enumeración, su generación, las propiedades del álgebra subyacente, la geometría que se deduce de las reflexiones en el espacio, etc.
Esta área de las matemáticas se ha visto fuertemente influenciada en los últimos años por el desarrollo de la informática. En cierto modo, la combinatoria sirve como puente entre el mundo de las matemáticas puras y el de la computación, pues muchas veces es necesario desarrollar herramientas teóricas con el fin de entender el funcionamiento de grandes estructuras discretas (como podría ser una red social, con millones de usuarios).
Para fortalecer la colaboración y los intercambios existentes entre estos distintos temas y las diferentes escuelas de combinatoria en Europa, el ICMAT acogerá entre día 27 y el 29 de noviembre el workshop Recent trends in algebraic and geometric combinatorics, que reunirá a unas 40 personas que trabajan en temas de investigación actuales en esta disciplina. El workshop se sustentará sobre 12 charlas de investigadores invitados, especialistas mundiales en su disciplina, que representan con sus ocho nacionalidades –principalmente, europeas- la diversidad y el dinamismo de este campo en el horizonte del continente. El workshop se focalizará en tres ejes principales: las aplicaciones de la combinatoria moderna en el álgebra, la combinatoria enumerativa y la geometría combinatoria.
Aplicaciones de la combinatoria moderna en el álgebra
La combinatoria permite interpretar de manera sencilla ciertas estructuras algebraicas, y recíprocamente, objetos algebraicos pueden formularse y estudiarse de manera más sencilla si se codifican usando objetos propios de la matemática discreta (como son, por ejemplo, los grafos y los árboles). La reciente evolución de áreas aparentemente tan dispares como la teoría de control, las ecuaciones en derivadas parciales estocásticas o el enfoque de Connes – Kreimer en relación a la teoría de renormalización en teoría cuántica de campos ha demostrado que muchos campos de las matemáticas comparten estructuras algebraicas comunes, y en el núcleo de este formalismo se hallan las estructuras algebraico-combinatorias de Hopf y de Lie. Han sido los trabajos de Rota y Joni, y posteriormente de Schmitt los que condujeron a la noción que tenemos hoy de Álgebra combinatoria de Hopf.
Combinatoria enumerativa
Otro problema fundamental en combinatoria es el del conteo. El problema de saber contar cuantas estructuras existen cumpliendo unas ciertas propiedades es central no sólo en la combinatoria, sino en distintas áreas de las matemáticas: saber contar bien cuantas permutaciones existen con ciertas obstrucciones, o cuantos diagramas con un número fijado de vértices se pueden dibujar en la esfera tiene implicaciones muy profundas en la teoría de representación de grupos, la teoría de los dessins d’enfants, la teoría de probabilidad, la física estadística y, por supuesto, la teoría de la computación.
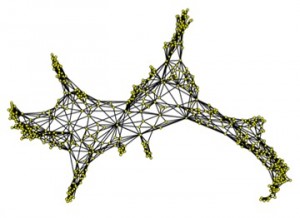
Muy recientemente se han realizado contribuciones muy importantes en esta dirección, y en la mayoría de estos casos la combinación de técnicas algebraicas (especialmente con la utilización de las denominadas funciones generatrices) con técnicas combinatorias han permitido describir con más claridad las estructuras combinatorias subyacentes de grandes objetos discretos. Este es el caso, por ejemplo, de los mapas planos, objetos que sirven de modelos discretos de la esfera
Geometría combinatoria
En el último de los ejes, la geometría combinatoria estudia objetos geométricos, como por ejemplo conjuntos de curvas en el plano. Muchas veces el leitmotiv de la geometría combinatoria está relacionado íntimamente con la combinatoria algebraica. Un ejemplo muy representativo de este paradigma es la teoría de politopos. Un polítopo no es más que la generalización geométrica de lo que habitualmente llamamos poliedro (es decir, un objeto geométrico convexo tridimensional cuyas caras son todas planas).
Uno de los mayores logros en el estudio de los politopos es el denominado f-theorema, que caracteriza los f-vectores de los politopos simpliciales o simples. Este resultado, conjecturado por McMullen in 1970, fue demostrado por Richard Stanley en el año 1980 con técnicas puramente algebraicas. Un ejemplo mas reciente es el estudio del asociaedro generalizado y de los abanicos que se deducen, motivado y relacionado con la teoria reciente de las denominadas algebras amontonadas, introducidas por Fomin y Zelevinsky. El workshop cubrirá estas conexiones entre geometría discreta y combinatoria algebraica.
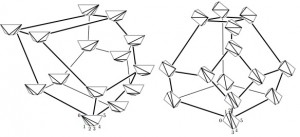
de las triangulaciones de un hexágono
Finalmente, dicha actividad se verá complementada con una charla pública del Profesor Speicher en el colloquio conjunto entre el ICMAT y del Departamento de Matemáticas de la UAM. Dedicaremos otro post en el blog para hablar especialmente de dicha charla y del Profesor Speicher.
Más información
http://www.icmat.es/RTAGC/
—
Kurusch Ebrahimi-Fard es investigador del ICMAT, Vincent Pilaud, es investigador del CNRS y de LIX, École Polytechnique (Francia) y Juanjo Rué es investigador de la Freie Universität Berlin y del Berlin Mathematical School (Alemania)

