Historias de pi: la cuadratura del círculo

Aplicando entonces

Una regla recta, procedo con las medidas

Hasta que el círculo se convierta en un cuadrado;

El centro del cuadrilátero es

La plaza del mercado, y hacia ese centro corren

Caminos rectos centrípetos; como una estrella,

Siendo ella misma por naturaleza circular,

tiene rayos de luz que irradian desde ella

Bastante rectos en todas las direcciones.

ARISTÓFANES: Las aves

 

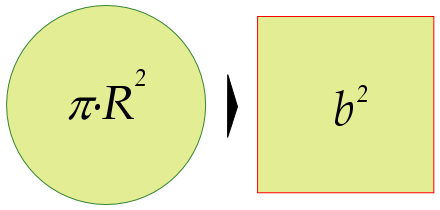
La cuadratura del círculo es un antiguo problema, que tiene sus rígenes en los geómetras de la antigua Grecia. Se trata de, dado un círculo, construir un cuadrado que tenga la misma área. La imposibilidad de hacerlo con regla y compás, lo que fue probado en el siglo XIX habiéndose resistido esa prueba por muchos siglos, llevó a que “lograr la cuadratura del círculo” fuera sinónimo de una tarea imposible.

Anaxágoras

 

En entradas anteriores nos hemos referido a los intentos de calcular el área de un círculo, así como la longitud de una circunferencia. Aquí nos vamos a referir al problema de la cuadratura en sí, que ya el propio Dante en La Divina Comedia daba por imposible

Como el geómetra aplica su mente

Para cuadrar el círculo, ni por todo su ingenio

encuentra la fórmula correcta, por más que lo intente

o Alexander Pope, en su Dunciada:

La locura de Mathesis no tenía límites,

Demasiado loca para que las meras cadenas materiales la aten,

Ahora levanta su mirada extática hacia el espacio puro,

Ahora, corriendo alrededor del círculo, lo encuentra cuadrado.

Según Plutarco, el primero en preocuparse por este problema fue Anaxágoras, durante uan estancia en prisión en Atenas alrededor del 430 a.C., en donde había acabado por impiedad con los dioses (había proclamado que el sol no era un dios, sino una enorme roca incandescente). Otros matemáticos que se ocuparon del problema fueron Hipócrates de Quíos, Antifonte, Bryson de Heraclea e Hipias de Élide. Arquímedes también realizó varios avances importantes intentando una prueba.

En la Edad Media se escribieron varios tratados sobre la cuadratura del círculo, y quizás el más elaboradofue el de Franco de Lieja (canciller y más tarde maestro de la escolanía de la Catedral de Lieja), en 1050, con su obra «De quadratura circuli».

Los intentos de probar la cuadratura del círculo van de la mano del cálculo del número pi, y fueron muchos los matemáticos que se ocuparon de esta tarea. Y también el estudio de la naturaleza del número pi, y es esto lo que condujo a la prueba de la imposibilidad de cuadrar un círculo usando solo regla y compás.

Dios midiendo el mundo con un compás

Hay que explicar lo que entendemos por una regla y como usarla. Esta se supone un segmento que permite extender cualquier otro indefinidamente, no es una regla como las que usamos habitualmente. Y el compás permite trazar circunferencias dados dos puntos, uno de los cuáles será el centro.

Y ahora viene el mayor avance en el problema, la introducción de la geometría analítica por René Descartes, en La Géométrie (1637), un breve tratado incluido en el Discurso del método publicado de forma anónima. La introducción de coordenadas permite construir un puente entre la geometría y el álgebra, de manera que una curva se puede interpretar como el conjunto de puntos que satisface una ecuación algebraica. Así, una recta en el plano se interpreta como una ecuación lineal con dos variables, x e y (ax+by+c=0); y una cicunferencia, como una ecuación de segundo grado (x2+y2+dx+ey+f=0).

Por lo tanto, construir con regla y compás se reduce a calcular intersecciones de rectas, de una recta con una circunferencia, o dos circunferencias. Es decir, a resolver sistemas de ecuaciones algebraicas, y en consecuencia, obtener los puntos correspondientes del plano.

La solución a nuestra historia tiene que esperar todavía más de dos siglos (hasta 1882), hasta que el matemático alemán Carl Louis Ferdinand von Lindemann pudo demostrar que π no es un número algebraico, sino transcendente. Recordemos que hay dos clases de números irracionales, los algebraicos, que son soluciones de ecuaciones algebraicas; y los trascendentes, que no lo son. Así que si pi es trascendente, la cuadratura del círculo no es posible usando solamente regla y compás.

______

Manuel de León (CSIC, Fundador del ICMAT, Real Academia de Ciencias, Real Academia Canaria de Ciencias, Real Academia Galega de Ciencias).

Compartir:

Entradas relacionadas

19 comentarios

  1. Gracias Manuel por esta pequeña reseña de la cuadratura. No conocía el asunto de Anaxagoras, que era amigo de Pericles y por eso le encarcelaron.
    Un abrazo
    Santi

Deja un comentario