![]()
Lecciones del Far East


Cultura y educación matemática
Es verdad que el concepto de Far, de lejano, es ahora muy diferente de que podía tenerse a finales del siglo XIX, durante la colonización del lejano oeste. Es el nuestro un mundo en el que todo está cada día más próximo e interconectado. Pero no es un mundo uniforme. Conviven (e incluso diríamos que se ven cada vez más forzadas a convivir, por la creciente interconexión) diversas culturas, con profundas diferencias en valores, costumbres, normas, estructuras… La convivencia supone, a veces, la convergencia; otras veces, el reforzamiento de la señas de identidad. Sea como sea, el Far East sigue estando muy lejos, culturalmente hablando.
A primera vista, las matemáticas, como creación humana, parecen no verse (o sólo en escasa medida) afectadas por la coexistencia de tan distintas visiones del mundo. Este sería un tema de debate para otro apunte del blog, sobre etnomatemáticas (que es algo que va más allá del estudio anecdótico de la forma de contar de ciertas tribus…). Un aperitivo: la comunicación del prof. B. Barton –uno de los ponentes al próximo Simposio sobre Paradigmas….– en el primer congreso internacional sobre etnomatemática, celebrado en Granada en 1998, y luego publicada en el Zentralblatt fur Didaktik der Mathematik (1999/2, pp. 55-58).
Por el contrario, no hay duda de que la diferencia cultural marca, y mucho, la enseñanza de las matemáticas. El trabajo de Kaiser-Leung-Romberg-Yaschenko en el International Congress of Mathematicians-ICM2002, sobre “International Comparisons in Mathematics Education” y los informes de los grupos de discusión DG11 del International Congress on Mathematical Education-ICME-10 (2004) y DG14, del ICME-11 (2008), sobre el mismo tema, plantean un abanico de temas relacionados con la influencia cultural, que van desde el análisis de los resultados de las distintas pruebas internacionales sobre rendimiento matemático (TIMSS, PISA) hasta la propia concepción del curriculum matemático, un asunto sobre el que se han organizado ya diversas conferencias internacionales en el Center for the Study of Mathematics Curriculum (CSMC), la primera de las cuales, celebrada en Chicago en el año 2005, contó con una nutrida participación de representantes asiáticos.
También influye la cultura en las creencias que subyacen en la elección, énfasis y uso por los profesores de distintas estrategias didácticas –la tradición docente de cada cultura, incluso de cada país–, un tema sobre el que quisiera aportar dos referencias que me son próximas: la reciente tesis de mi antigua alumna de la Universidad de Cantabria, Raquel Vallines Mira, sobre estrategias didácticas en la enseñanza de las matemáticas a los indios norteamericanos; y el proyecto METE (Mathematics Education Traditions of Europe), financiado por la Unión Europea, en el que participa otro antiguo alumno, José Manuel Diego Mantecón, bajo la dirección de Paul Andrews (Facultad de Educación, U. Cambridge).
Como señala el mismo P. Andrews, la influencia cultural se aprecia, incluso, en el diseño de los recursos tecnológicos en la enseñanza de las matemáticas. Así, en una conversación privada con él, tras su conferencia plenaria en CADGME 09, me señalaba cómo hay argumentos culturales (lingüísticos, concepciones diversas de la educación, en general, y de las matemáticas, en particular) que subyacen al hecho de que, en algunos programas de geometría dinámica como Cabri (Cabrilog, creado en la Universidad de Grenoble) o GeoGebra (creado en la Universidad de Salzburgo), primero se selecciona una herramienta (regla, compás, etc.) en el menú y luego esta se aplica a unos elementos geométricos ya creados: por ejemplo, se selecciona “distancia” y, a continuación, se hace click sobre un par de puntos. Sin embargo, en el programa Sketchpad (Key Curriculum Press, USA), primero se ha de seleccionar el par de puntos para acceder luego a la herramienta de medida…
Enseñar en la frontera
Ahora bien, el estudio de las influencias culturales en la educación matemática no es sólo un atractivo tema de investigación para profesionales de la didáctica. Tampoco el conocimiento del medio humano y natural era, para los pioneros del Far West, una materia restringida a antropólogos y naturalistas, sino una cuestión de supervivencia. Ocurre que, en este mundo globalizado, estamos realmente enseñando matemáticas en la frontera, expuestos –en virtud de las distintas pruebas internacionales de rendimiento escolar y por la creciente desaparición de fronteras en la actividad económica—a la comparación con los resultados y métodos de los otros…
Y, en esa frontera metafórica de la que estamos hablando, varios de los países del Far East (China-Taiwan-Macao-Hong Kong, Corea, Japón, Singapur, India, Nueva Zelanda, Australia, etc.). tienen mucho que enseñarnos, al ocupar, de forma reiterada, los primeros puestos en las pruebas TIMMS y PISA, desde hace años.
Así, el Informe Ejecutivo del año 2007 (emitido en Diciembre de 2008) correspondiente al test internacional TIMSS (TIMSS International Mathematics Report 2007), que abarca medio centenar de países y que estudia el conocimiento matemático y científico de los alumnos de 10 y 14 años, respectivamente, desde hace una docena de años, señala lo siguiente:
«Mathematics Achievement
At the fourth grade, Hong Kong SAR and Singapore were the top performing countries. They were followed by Chinese Taipei, that had higher average mathematics achievement than all countries except Hong Kong SAR and Singapore, and, in turn, by Japan, that had higher achievement than all of the remaining countries./….
At the eighth grade, Chinese Taipei, Korea, and Singapore had the highest average mathematics achievement. These three countries were followed by Hong Kong SAR and Japan, also performing similarly and having higher achievement than all the other countries except the top three performers. There was a substantial gap in average mathematics achievement between the five Asian countries and the next group of four similarly performing countries, including Hungary, England, the Russian Federation, and the United States….»
Y, para ilustrar someramente nuestro argumento en el caso de PISA, véase, por ejemplo, la siguiente tabla:
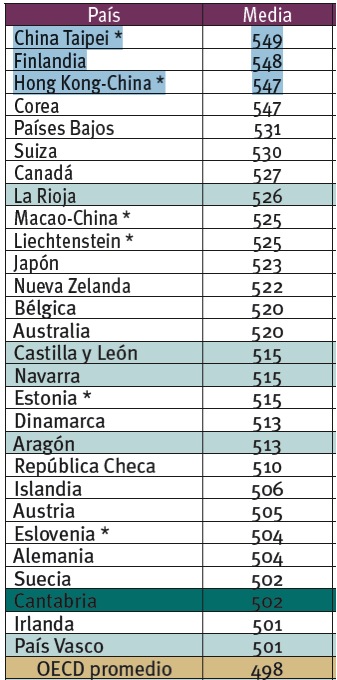
Resultados por encima de la media en competencia matemática, PISA 2006. (Fuente: “Evaluación PISA 2006. Resumen de los primeros resultados en CANTABRIA” Consejería de Educación de Cantabria. 2007).
Estos son, precisamente, algunos de los países cuyas peculiaridades en materia de educación matemática serán expuestas en el Simposio Paradigmas en la educación matemática para el siglo XXI: compartiendo experiencias educativas con Asia (Valencia, 22-24 de octubre de 2009). Junto a ellos, algunos otros países que nos son, culturalmente, más próximos (Portugal, EEUU, Francia, Reino Unido, Hungría, Finlandia), porque las distancias se aprecian mejor desde un paisaje con relieve…
El interés –y en el caso de Estados Unidos, la fascinación—de los países occidentales por la enseñanza de las matemáticas en el lejano oriente viene de lejos, aunque tal vez sea esta la primera ocasión que se materializa en nuestro país. Aportemos algunos datos recientes:
1-La publicación, por parte de la International Commission on Mathematical Instruction (ICMI), del estudio Mathematics Education in Different Cultural Traditions – A Comparative Study of East Asia and the West: The 13th ICMI Study, eds: Frederick K.S. Leung, Klaus-D. Graf and Francis J. Lopez-Real (Springer, 2006).

2-El informe del National Mathematics Advisory Panel, una comisión creada por la administración educativa americana en 2006 (por una orden ejecutiva del Presidente de los EEUU), con el fin de proponer acciones estratégicas para mejorar la enseñanza de las matemáticas en USA. El informe final ha visto la luz en marzo 2008. Es relevante contemplar que en dicho informe final hay 10 referencias elogiosas a los resultados sobre la enseñanza de las matemáticas alcanzados en Singapur, 4 referencias a Japón, 3 a Corea, 5 a China, pero ninguna a Francia, Alemania o Finlandia, por poner ejemplos de países europeos de larga tradición matemática. El modelo educativo asiático suscita más interés en los EEUU que el europeo, en estos momentos.
3-Los Angeles Times, 9 de marzo de 2008: In L.A., Singapore math has added value. El artículo aporta pruebas sobre la mejora en los resultados tras la introducción del modelo Singapur en la enseñanza de las matemáticas en una escuela de Los Angeles.
«….In 2005, just 45% of the fifth-graders at Ramona Elementary School in Hollywood scored at grade level on a standardized state test. In 2006, that figure rose to 76%. What was the difference?
If you answered 31 percentage points, you are correct. You could also express it as a 69% increase. But there is another, more intriguing answer: The difference between the two years may have been Singapore math.
At the start of the 2005-06 school year, Ramona began using textbooks developed for use in Singapore, a Southeast Asian city-state whose pupils consistently rank No. 1 in international math comparisons. Ramona’s math scores soared….»
4-Discurso, publicado en el Denver Post, del (entonces) candidato Obama, pronunciado en Thorton(Colorado), el 28 de mayo de 2008, presentando su programa educativo. Hace referencia específica a la situación de la enseñanza de las matemáticas en USA y a la ventaja potencial de China…
«…In this kind of economy, countries who out-educate us today will out-compete us tomorrow. Already, China is graduating eight times as many engineers as we are. By 12th grade, our children score lower on math and science tests than most other kids in the world. And we now have one of the highest high school dropout rates of any industrialized nation in the world. …»
5-The New York Times, 10 de octubre, 2008: Math Skills Suffer in U.S., Study Finds
El artículo menciona la abrumadora presencia de chicas de origen asiático en el equipo estadounidenses de las olimpíadas matemáticas internacionales.
«….United States girls’ team that began competing in the Girls’ Math Olympiad….Thirteen girls from the United States have competed in the last two years, according to the study, and all are of Asian descent except one,…»
6-Artículo de Le Monde, 11 de diciembre de 2008, como reacción a la publicación de los resultados de TIMSS 2007, titulado: Les élèves asiatiques sont les meilleurs en mathématiques et en sciences.
7- La existencia de revistas de educación matemática especializadas en las relaciones Oriente-Occidente, como el Journal of Mathematics Education (JME), cuyo primer número es de diciembre de 2008.
8- El editorial de la ICMI-News, del pasado junio de 2009, que versa, precisamente, sobre Mathematics Education in East Asian Countries.
Enseñar….y aprender
Posiblemente el sufrido lector que haya consultado los distintos documentos enlazados hasta aquí estará convencido de que en el Simposio Paradigmas en la educación matemática para el siglo XXI: compartiendo experiencias educativas con Asia los países del lejano oriente tendrán mucho que enseñarnos. Pero, ¿tendremos, nosotros, mucho que aprender? ¿Qué podremos aprender, en la práctica, de culturas tan lejanas. ¿Será posible trasladar a nuestro contexto alguna de las cosas que escuchemos en el Simposio? Puedo imaginar varios tipos de obstáculos, pero creo que la asistencia al Simposio será la ocasión de dilucidar esta incógnita.
Sin embargo, no me resisto a terminar este apunte sin una última reflexión. En el editorial de ICMI-News al que me he referido arriba, el profesor Leung (uno de los invitados al Simposio) se refiere a lo que el denomina la Paradoja del estudiante chino. A pesar de los excelentes resultados, las condiciones materiales y pedagógicas en los países de tradición confucionista, comenta el, son malas: las clases tienen demasiados alumnos, la docencia es muy tradicional y apenas permite la participación del alumno. Pero también menciona otros problemas, que no se pueden resolver con medios humanos y materiales.
Por ejemplo, en nuestra sociedad suele ir unido el rendimiento escolar en matemáticas con el aprecio por las matemáticas y con un grado alto de autoconfianza en su dominio. Los alumnos que tienen cierta seguridad y disposición para las matemáticas suelen rendir mejor que aquellos que se consideran con dificultades para las mismas (y recíprocamente). Sin embargo, tanto en ese editorial ICMI-News como en el artículo de Kaiser-Leung-Romberg-Yaschenko citado arriba, y también en los posteriores informes PISA, se aprecia1 que esta correlación no se da en muchos países del Lejano Oriente, en los que parece que la sociedad considera inapropiados ciertos niveles de autoafirmación en el individuo que, por el contrario, son apreciados como positivos en la nuestra. Es curioso constatar que en el informe PISA 2003 (el último en el que las matemáticas eran el tema principal de análisis), eran los estudiantes de los EEUU los que mostraban más seguridad en su capacidad para entender cuestiones difíciles de matemáticas, y los japoneses y coreanos, los que menos (justamente al contrario de lo que mostraba el resultado de las pruebas).
Este tipo de comportamiento, ligado a la cultura, es difícilmente exportable. Se dirá que tampoco es conveniente….Pero, lo que está detrás de la humildad colectiva que describe la Paradoja del estudiante chino es la idea de que el éxito escolar no se debe tanto a la inteligencia, sino a la capacidad de trabajo y, por tanto, al alcance de cualquiera. Las matemáticas son difíciles, pero si trabajamos duramente…
Tal vez esta lección sí que podríamos aprenderla…
____________________________________________________
1 Students’ Attitudes towards Mathematics
… although the TIMSS-R results were consistent with the findings from the literature that students’ positive attitudes towards mathematics was related with higher achievement within a country, the same relationship did not hold across countries. In fact, with the exception of Singapore, all the topperforming countries had relatively negative attitudes towards mathematics.
In particular, across countries, a positive self-concept in mathematics did not seem to be related with higher achievement. It is noticeable that students from all the five top-performing East Asian countries had very low self-image of mathematics. This suggests that self-image of mathematics or confidence in doing mathematics may be related to cultural values and is not necessarily associated with student achievement.
2 …On average across OECD countries, 67 per cent of students disagree or strongly disagree that in their mathematics class, they understand even the most difficult work. Countries vary with respect to the response patterns. For example, for the aforementioned question, percentages disagreeing or strongly disagreeing range from around 84 per cent or more in Japan and Korea to 57 per cent or less in Canada, Mexico, Sweden and the United States. Similarly, on average across OECD countries, roughly half of the students disagree or strongly disagree that they learn mathematics quickly. But while in Japan and Korea, as well as in the partner country Thailand, more than 62 per cent of students disagree or strongly disagree, the proportion is only around 40 per cent of students in Denmark and Sweden…
Nota: Las ilustraciones provienen de
http://www.fotolog.com/farwestrodeo/27779809,
http://www.udc.es/dep/pdce/EdelaTorre.htm,
http://www.casaasia.es/matematicas/esp/index.html,
htpp://books.google.es,
http://geogebra.es/cvg/06/index.html
Tomás Recio, Universidad de Cantabria
