![]()

El procesamiento de imágenes digitales y su relación con la teoría de muestreo y las ecuaciones en derivadas parciales
Uno de los usos más importantes y útiles del procesamiento de imágenes en la tecnología hoy en día puede ilustrarse con los satélites Landsat. Estos son una serie de satélites que orbitan alrededor de la tierra en una órbita circular grabando imágenes del terreno y de las costas de modo que cualquier lugar del planeta se pueda testear con imagenes cada 8 días. Las imágenes obtenidas por estos satélites son útiles para estudiar el ritmo y la dirección del crecimiento urbano por ejemplo. La comunidad agropecuaria las utiliza para analizar la humedad del suelo y clasificar la vegetación. En cuanto a los gobiernos, estos pueden detectar y estimar los daños provocados por desastres naturales; y, los organismos de protección del medio ambiente para identificar la contaminación realizada por chimeneas y medir la temperatura del agua de ríos y lagos cercanos a plantas de energía.
Los sensores que están incorporados en los satélites sacan siete imágenes simultáneamente de una región de la Tierra que se quiera estudiar. Cada imagen se digitaliza y se guarda en una matriz rectangular, donde cada entrada es un número que indica la intensidad de señal de un punto (o pixel) de la imagen.
Dichas imágenes suelen tener mucha información redundante, la cual ocupa espacio y uno trata de comprimirla para que esto no ocurra, pero tal compresión puede provocar que la imagen resulte ilegible. Una de las técnicas más utilizadas hoy en día para este problema de compresión de imágenes es lo que se conoce como descomposición en valores singulares; correspondiente a uno de los tantos estudios que se realiza en lo que se conoce en matemáticas como el álgebra lineal numérica; pero de este tema nos encargaremos en otra entrada para este blog.
El problema del procesamiento de imágenes tuvo un gran auge a fines de los 80′ y hoy es algo que está incorporado a la vida diaria. Uno saca una foto y después procesa la imagen y la modifica. La contrasta, le pone o quita brillo, le quita los ruidos, le cambia el fondo, el color, etc.
Nuestro enfoque tiene sus comienzos a fines de los años 40′ con la teoría de Nyquist-Shannon para el procesamiento de imágenes orientado a la compresión. Luego, Gabor en los años 60′ demostró como la anterior formulación tenia su relación con las ecuaciones en derivadas parciales, mas precisamente, con la ecuación del calor.
Un sensor de captura de imágen es el elemento de una cámara fotográfica digital que capta la luz que compone la fotografía.
Estos chips semiconductores tienen una matriz rectangular de dispositivos (llamados photosites) donde cada uno es sensible a tres colores, rojo, verde y azul (conocidos como colores RGB debido a red, green, blue). La sensibilidad es lograda por solo uno de los colores RGB por filtración. Estos sitios se organizan en la matriz RGB de Bayes.
Observemos que dicha matriz, contiene mas lugares verdes (un 50% del total). Esto se debe a que el ojo humano cuenta con mayor sensibilidad al color verde.
Antes del procesamiento de la imagen la matriz de Bayes se interpola depende el tipo de imagen que queramos (por ejemplo si en nuestro menú de la cámara ponemos imagen natural, o blanco y negro, colores vivos, etc.) y luego se guarda la imagen.
Lo mas común es el balance de grises, mejora del contraste, quitar el ruido y comprimir los datos como mencionamos anteriormente. Por simplicidad nosotros solo comentaremos lo que sucede cuando se trabaja con un solo canal en lugar de tres, es decir, trabajaremos con imágenes en blanco y negro. Y nuestro interés cae precisamente sobre el problema del desenfoque y eliminación de ruido en las imágenes y la compresión, donde el principal problema es que los bordes de las partes que forman la imágenes no sean destruidos por las modificaciones que hagamos.
La figura del bebé nos ilustra como se altera la imagen utilizando la teoría de muestreo (tomando submuestreos) para comprimir la imagen. Se piensa a la imagen como un conjunto de muestras y se toma un submuestreo del mismo donde existe una relacion entre las submuetras que se toman con respecto a la muestra original. Pero se puede observar que cuanto mas se incrementa esa distancia entre las submuestras que se toman del muestreo original la imagen se va desconfigurando y, lo mas importante, los bordes se ven muy afectados! Como observamos en la imagen anterior, por ejemplo la ultima imagen corresponde a tomar 1 punto de cada 35.
Shannon se dió cuenta que antes de tomar el submuestreo de la muestra habia que aplicarle a la imagen lo que se conoce en matemáticas como suavizante gaussiano o smoothing. Para los que estan más familiarizados con las operaciones de funciones en el análisis matemático, Shannon comprendió que convulocionar la imagen original con una función gaussiana y luego tomar el submuestro llebava a un resultado mucho mejor como vemos en la siguiente figura.
La primer parte de la figura corresponde a la imagen original, la segunda al aplicarle el suavizante a la imagen original. La tercera imagen corresponde al tomar un submuestreo de la original y la última a tomarlo en la imagen ya suavizada. Como observamos Shannon estaba en lo correcto. Si suponemos que se aplica un suavizante gaussiano a la imagen original antes del submuestreo los resultados para la compresion de la imagen son mucho mejores.
Esta hipótesis de suavidad es necesaria para la formulación del problema en ecuaciones en derivadas parciales. Mas aún, es la clave de esta formulación dada por Gabor en los 60′. Lo que Gabor demostró fué que la diferencia entre la imagen ya suavizada y la original es rápidamente proporcional al Laplaciano de la imagen original. Es decir, si denotamos por u_0 a la imagen original y k al suavizante gaussiano (como función radial)
Entonces el proceso de suavización se traduce en resolver
Del mismo modo, Gabor dedujo, que en cierta medida se puede «enfocar» la imagen tratando al problema como un problema inverso en el tiempo resolviendo,
La figura muestra la imagen original y la imagen obtenida luego de hacer la convolución de la imagen con el suavizante gaussiano.
Numéricamente el problema inverso puede tratarse como
Esta operación puede repetirse varias veces para h‘s pequeños pero el algoritmo explota rápidamente.
La última imagen muestra el algoritmo de Gabor aplicado a la imagen original para enfocarla. La primera es la original, la segunda luego de cuatro pasos del algoritmo y vemos como queda la imagen (destrozada) luego de 10 pasos del algoritmo. En cambio esto no sucede si aplicamos el suavizante gaussiano k antes de aplicar el algoritmo.
La figura nos muestra el algoritmo de Gabor para 4 y 10 pasos para el enfoque de la imagen cuando la imagen fue suavizada previamente.
Otra cuestión importante es la eliminación del ruido en las imágenes. Para darnos una idea de lo que es el ruido de una imagen observemos la siguiente imagen, la cual se expone con un 75% de ruido y luego la imagen reconstruida al suavizarla.
Las imágenes, digitales en casi todos los casos, tienen ruido. Vamos a considerar acá que el ruido es aditivo y Gaussiano. Cuando se mira el estado de frecuencia de una imagen (si investigan casi todas las cámaras digitales de hoy tienen una función que muestra el ruido de la imagen), el ruido corresponde a altas frecuencias. Para eliminarlo se han usado varias técnicas, pero el inconveniente es que los bordes corresponden a altas frecuencias y es por ello que por lo tanto los bordes también son afectados.
Una idea original fué la introducción de la ecuación del calor para el tratamiento de imágenes. Veamos como el ruido y el calor se asocian en una sola cuestión.
Supongamos que tenemos una habitación con una fuente de calor en el centro. Al pasar el tiempo el calor se propaga por la habitación en círculos concéntricos. Estos círculos van perdiendo magnitud a medida que se propaga el calor. Es decir, el calor avanza alejándose de la fuente y va perdiéndose. Esto se debe a que la temperatura de la habitación tiende a homogeneizarse.
Ahora supongamos que esta fuente de calor existe en un instante puntual y luego de ese instante deja de emitir calor. A medida que la temperatura aumenta hacia afuera, va disminuyendo en el centro. Es decir, el calor tiende a uniformarse, pero esta ves a una temperatura intermedia entre la temperatura original de la habitación y la de la fuente.
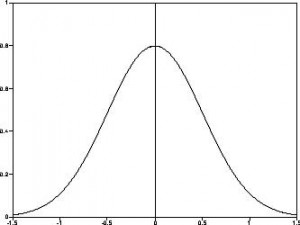
Finalmente, pensemos la habitación como una imagen y que esta fuente puntual e instantánea es un punto originado por un ruido aditivo. Para simplificarlo asumimos también que hay un único punto de ruido. Si aplicamos el mismo concepto de calor al ruido, podemos imaginarnos como este ruido va propagándose y disminuyendo su intensidad . Desde otro punto de vista, si hacemos un corte transversal de la imagen podemos ver el ruido como una Gaussiana. Es decir, si seguimos con la idea de tratar al ruido como un punto de emisión de calor, la evolución a través del tiempo puede verse como la siguiente gráfica de una función
Cuando el tiempo crece la imagen se vuelve poco interesante porque se van uniformizando todas las particularidades. Ese enfoque equivale a hacer la convolución de la imagen con gaussianas de media cero y varianza variable definida en función del tiempo.
Pero, este razonamiento tiene un inconveniente. El ruido se reparte uniformemente en la imagen y los bordes corresponden a la categoría de ruidos. Entonces nos topamos con las mismas dificultades del tratamiento clásico con la teoría de Shannon. Pero todo esto lo podemos extender para aprovechar las propiedades de la ecuación del calor. La idea es manipular los coeficientes que conducen el calor.
Sabemos que el calor no se propaga de la misma manera en distintos medios. Hay materiales que conducen mejor el calor que otros. Volviendo al ejemplo de la habitación, supongamos que dividimos dicha habitación con un panel y que en cada lado hay una fuente que conduce calor y suponemos también que el material NO conduce calor. El calor no se propaga del otro lado de la habitación y cada parte tiende a encontrar un balance térmico independiente del de la otra parte de la habitación. Esto es porque el coeficiente de conducción de calor del panel es cero.
Como uno puede ver, una imagen esta formada por regiones delimitadas por bordes y queremos encontrar un método que difumine el ruido dentro de las regiones sin afectar a los borde. Entonces ya tenemos la solución! Si consideramos que el coeficiente de conducción de calor varia entre 0 y 1; asignándole a las regiones delimitadas por los bordes un 1 y a los bordes un 0 tendríamos el problema solucionado.
Este problema es de gran importancia en el ámbito de las ecuaciones diferenciales parciales, conocido como “difusión” o “difusión anisotrópica”, y comenzó a estudiarse por Pietro Perona y Jintendra Malik en el artículo “Scale-Space and Edge Detection using Anisotropic Diffusion” publicado en 1990.
Ellos proponen la siguiente ecuacion de difusion anisotrópica
donde div indica el operador divergencia,
los operadores gradiente y laplaciano respectivamente en las variables espaciales; g es una función positiva, continua, que en el infinito tiende a cero y en cero tiende a 1.
La función g es escogida tipicamente como las funciones de Lorentz o Leclerc y debido a que
juega el rol de detector de bordes pero este tiende a infinito rapidamente, sumado a las propiedades que debe cumplir esta funcion se expresan como
Para finalizar nuestro estudio quiero destacar que existe una gran diferencia en el tratamiento de imagenes digitales e imagenes artificiales. La principal diferencia se debe a que las imágenes artificiales se realizan con bordes suaves, con lo cual no hay discontinuidades en la derivada, lo cual complica el tratamiento. Esta complicación si pasa con la imagenes digitales naturales. Nuestro estudio combate con esta y la supera.
Para ilustrar esto observemos la diferencia en estas dos imagenes, una artificial y la segunda, correspondiente al cerro Torre en la Patagonia, Argentina, una imagen natural.
____________
Leonardo Colombo es investigador predoctoral del Instituto de Ciencias Matemáticas.





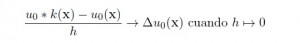
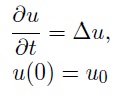
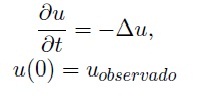

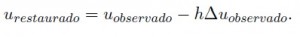








la verdad leo! es que sos un genio!!!! muy buen informe!!!!
Leo! te felicitamos 🙂 sos un capo,
Besos
Los chicos.
Leo….excelente informe!!!! Felicitaciones…
Muy bueno el articulo, felicitaciones Leo. Luis
Muy bueno el articulo, felicitaciones. Luis