![]()
La extinción de los apellidos entre la aristocracia victoriana y el número R
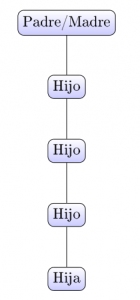
En la segunda mitad del siglo XIX surgió una curiosa preocupación entre la aristocracia victoriana sobre la posible extinción de sus apellidos. Para entender el problema, comencemos recordando que esos apellidos se transmitían desde el padre (no madre) a los hijos, tanto varones como hembras, pero luego eran sólo los hijos varones quienes los volvían a transmitir.
Una representación esquemática de la transmisión de apellidos siguiendo la línea masculina. Sólo los hijos varones transmiten el apellido.
Esta preocupación tuvo eco entre los estadísticos de la época, como muestra el hecho de que sir Francis Galton (Birmingham, 1822 – Haslemere, 1911) propusiera en la revista The Educational Times and Journal of the College of Preceptors, el 1 de marzo de 1873, la siguiente cuestión:
“Question 4001 (Proposed by FRANCIS GALTON) — A large nation, of whom we will only concern ourselves with the adult males, N in number, and who each bear separate surnames, colonise a district. Their law of population is such that, in each generation, a0 per cent. of the adult males have no male children who reach adult life; a1 have one such male child; a2 have two; and so on, up to a5 who have five. Find (1) what proportion of the surnames will have become extinct after r generations; and (2) how many instances there will be of the same surname being held by m persons.
[The Proposer remarks that a general solution of this problem would be of much aid in certain rather important statistical enquiries, and that he finds it a laborious matter to work it out numerically, in even the simplest special cases, and to only a few generations. In reality, the generations would overlap and mix, but it is not necessary to suppose them otherwise than as occurring in successive steps.]”

El reverendo, y matemático, Henry William Watson (Marylebone, 1827 – Berkswell, 1903) aceptó el desafío y propuso una solución en la misma revista el 1 de agosto de 1873. A raíz del intercambio de ideas entre ellos, publicaron un artículo conjunto titulado «On the probability of the extinction of families» en 1875, en la revista Journal of the Royal Anthropological Institute of Great Britain and Ireland, con la solución a la cuestión de Francis Galton. Aunque los autores no eran conscientes de ello, con ese artículo Francis Galton y Henry William Watson habían redescubierto el trabajo previo del estadístico francés Irénée-Jules Bienaymé (París, 1796 – París, 1878) sobre la extinción de familias cerradas (aristocráticas, por ejemplo), motivo por el cual hoy el proceso es conocido como proceso de Galton-Watson, pero también como de Bienaymé-Galton-Watson.

Puede ser interesante construir el proceso en un contexto general para que el lector luego pueda identificar otras aplicaciones que no sean la original de Francis Galton a su problema.
Consideremos una población de individuos que cambia su configuración en instantes discretos de tiempo n = 0, 1, 2, … – denominados generaciones – y que, con independencia de la naturaleza de los individuos – personas, organismos, neutrones, genes – lo hace de la siguiente manera:
- Cada individuo de la generación n produce un número aleatorio de nuevos individuos, denominados descendientes, en la generación n+1.
- La secuencia Xa, Xb, … formada por los números de descendientes para cada individuo a, b, … está formada por variables aleatorias mutuamente independientes, que son también independientes de los números de descendientes de individuos en las generaciones previas.
- Los números Xa, Xb, … también son idénticamente distribuidos con función de masa común F = {Pk: k=0,1, …}, donde Pk = P{ Xa = k }.
Es decir, la ley de probabilidad que determina el tamaño Xa de la descendencia de un individuo – el individuo a – de la generación n es la misma que la correspondiente ley para cualquier otro individuo de esa u otra generación, y su realización – por ejemplo, el individuo a de la generación n genera k descendientes – no depende del número de descendientes generados por el resto de los individuos de la generación n a la que pertenece o de las generaciones previas. Siguiendo esta descripción, el estado Zn del proceso de Galton-Watson en el instante n es el número de individuos en la generación n.
En el problema original de Francis Galton, Zn representa el número de apellidos iguales al del antecesor inicial presentes en la población en la generación n por herencia a lo largo de la línea masculina. En esta contabilidad sólo se contabilizan los apellidos de los varones, no de las hembras, dado que éstas no transmitirán su apellido en generaciones futuras. El hecho de asumir un único antecesor inicial está vinculado a suponer Z0 = 1.
Comenzando desde Z0 = 1, el estado del proceso en la generación n+1 se obtiene desde la recursión
Zn+1 = X1(n+1) + … + XZn(n+1),
que expresa el número de descendientes en la generación n+1 desde la contribución (a esa generación n+1) del i-ésimo individuo – es decir, Xi(n+1) – de la generación n. El número de descendientes en la generación n es una variable aleatoria Zn que podría tomar el valor 0, en cuyo caso Zn+1 = 0 y, como consecuencia, Zm = 0 en cualquier generación posterior m = n, n+1, … Es importante destacar que la independencia de las variables aleatorias Xi(n) garantiza que la sucesión {Zn: n=0,1,…} verifica la propiedad Markoviana.
No todas las elecciones de la distribución de descendencia F conducen a un proceso de Galton-Watson interesante. Por ejemplo, si F está concentrada sobre un único punto (es decir, Pk = 1 para un cierto número k), entonces el proceso es determinista y Zn es el producto de k consigo mismo n veces.
 El proceso de Galton-Watson determinista, cuando el número de hijos varones es siempre igual a 1.No olvidemos que las hijas no influyen en la herencia del apellido.
El proceso de Galton-Watson determinista, cuando el número de hijos varones es siempre igual a 1.No olvidemos que las hijas no influyen en la herencia del apellido.
Otro proceso poco interesante se tiene cuando F está concentrada sobre los puntos k = 0 y 1, de modo que P0, P1 > 0 y P0 + P1 = 1. En este caso, la población permanece en el estado inicial Z0 = 1 durante un cierto número n’ de generaciones – con probabilidad igual al producto de P1 consigo mismo n’ veces – y luego salta al estado 0 en la siguiente generación n’+1 – con probabilidad P0 –, donde permanece indefinidamente. El estado 0 es, entonces, absorbente y refleja la extinción del proceso en la generación n’+1.
Supervivencia de un apellido durante n’ = 3 generaciones (sin incluir la inicial) y extinción en la 4ª generación.
Para evitar estos casos particulares, el análisis del proceso de Galton-Watson está habitualmente asociado a la hipótesis de que la distribución de descendencia no está concentrada sobre un único punto (por ello, Pk < 1 para todo k) y asigna probabilidad estrictamente positiva (Pk > 0), al menos, a algún k > 1. En tal caso, un sencillo cálculo conduce a una expresión para el tamaño medio de la población en la generación n en términos de
E[Zn] = M·…·M,
es decir, el producto del tamaño medio M de la descendencia de un individuo consigo mismo n veces.
El valor de M tiene propiedades interesantes y permite clasificar los procesos de Galton-Watson como supercríticos (M > 1), críticos (M = 1) y subcríticos (M < 1), de manera que la extinción del proceso se observa con seguridad en los casos crítico y subcrítico, mientras que el proceso puede no extinguirse en el caso supercrítico con probabilidad positiva.
Estos últimos comentarios nos llevan a ver una clara similitud entre el tamaño medio M de la descendencia de un individuo en el proceso de Galton-Watson y el factor reproductivo básico R0 de los modelos epidémicos, como puede observar el lector comparando esta entrada con otras entradas recientes sobre las matemáticas del coronavirus, y las matemáticas contra la malaria y el modelo SIR. Esa similitud no es casual, dado que el proceso de Galton-Watson tiene aplicaciones a la trasmisión de enfermedades infecciosas en sus fases iniciales de propagación.
Entre las aplicaciones modernas se encuentra la proliferación de neutrones libres en una reacción de fisión nuclear, desde los trabajos de Leo Szilard a finales de 1930. Pero no hay que olvidar la genética, sin duda la más cercana al trabajo de Francis Galton y Henry William Watson que nos permite explicar por qué un reducido número de individuos, antepasados de Homo sapiens, tienen ahora descendientes sobrevivientes de la línea masculina reflejados en un número bastante pequeño de haplogrupos distintivos de ADN del cromosoma Y humano.
—
Mario Castro Ponce (Universidad Pontificia Comillas), Manuel de León (Instituto de Ciencias Matemáticas CSIC, Real Academia de Ciencias) y Antonio Gómez Corral (Universidad Complutense de Madrid)