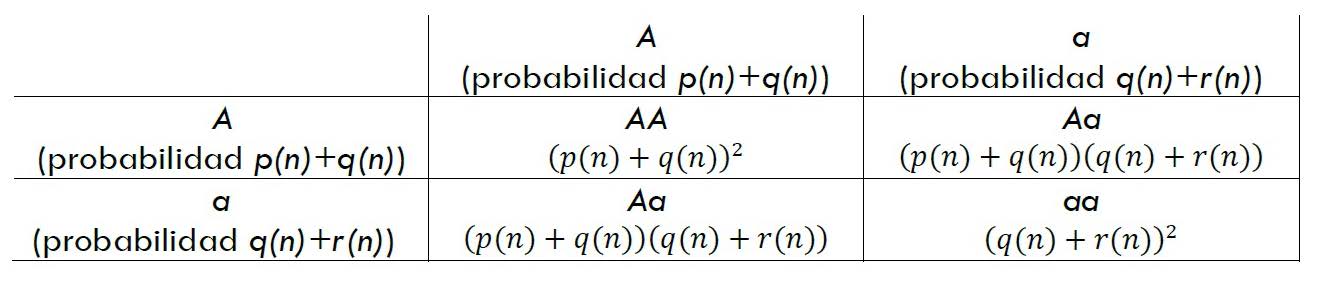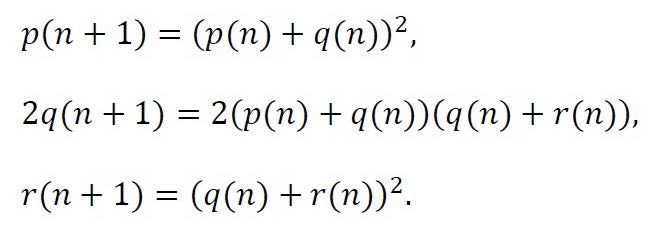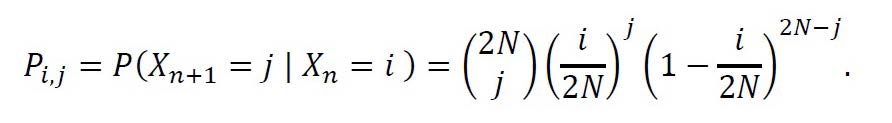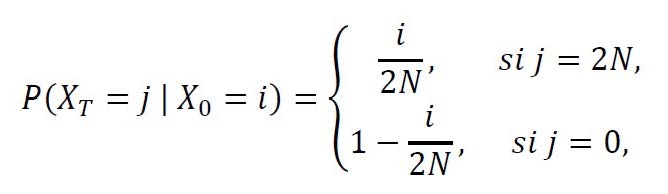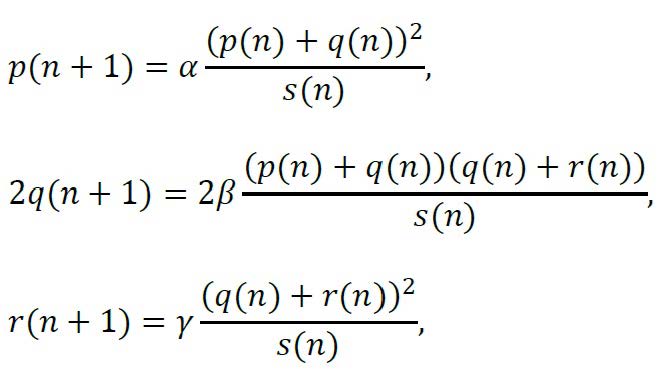![]()
Cadenas de Markov y las leyes de Mendel (II)
En esta entrada, más técnica de lo habitual, vamos a emplear uno de los problemas más clásicos y famosos de la Biología, el descubrimiento de las leyes de la herencia, para explicar a nuestros lectores el uso de las cadenas de Markov en Biología Matemática. En nuestros comentarios aparecerán el monje checo Johann Mendel y otros dos eminentes matemáticos británicos, Godfrey Harold Hardy y Ronald Aylmer Fisher.
Gregor (Johann) Mendel (Heinzendorf, 1822 – Brünn, 1884)
Los guisantes de Johann de Mendel
El término Leyes de Mendel fue por primera vez empleado a raíz de que el holandés Hugo de Vries, el alemán Carl Correns y el austríaco Erich von Tschermak redescubrieran, de manera independiente y casi simultánea en 1900, los postulados del monje agustino sobre la herencia, como ya mostramos en la entrada Mendel, el de los guisantes. Estos postulados están basados en los experimentos realizados entre los años 1856 y 1863 por Johann Mendel sobre la variabilidad de las plantas de guisantes, y aparecen descritos en el artículo titulado “Versuche über pflanzenhybriden” (“Experimentos sobre la hibridación de las plantas”), que presentó en dos sesiones de la Sociedad de Historia Natural de Brno en 1865 y publicó en la revista Verhandlungen des Naturforschenden Vereines in Brünn en 1866. La traducción al inglés de este trabajo forma parte del documento “Mendel’s Principles of Heredity: A Defence” (“Los Principios Mendelianos de la Herencia: Una Defensa”) escrito por el británico William Bateson en 1902 con la intención de clarificar el papel de Johann Mendel como precursor de la Genética moderna.
Johann Mendel explicó sus observaciones y su patrón de la herencia tomando como sistema modelo a los guisantes de jardín (Pisum sativum) y sus características fenotípicas, aprovechando que estas plantas tienen un rápido ciclo de vida, producen un elevado número de semillas – fáciles de catalogar por su forma (en concreto, color y rugosidad) – y se pueden reproducir por autofecundación, además de que también son fáciles de cruzar o aparear de forma controlada. En concreto, al cruzar plantas nacidas de semillas lisas con plantas nacidas de semillas rugosas, observó que las plantas híbridas obtenidas siempre generaban semillas lisas, lo cual le llevó a acuñar los términos dominante y recesivo para referirse a los rasgos “semilla lisa” y “semilla rugosa”, respectivamente. De manera semejante llegó a catalogar el rasgo “semilla amarilla” como dominante y el rasgo “semilla verde” como recesivo.
Desde un primer experimento, Johann Mendel observó que, con independencia del carácter fenotípico en estudio,
la autofecundación de las plantas nacidas desde semillas híbridas producía en la primera generación semillas que tenían bien el rasgo dominante o el rasgo recesivo en proporciones aparentemente aleatorias,
y concluyó que
las semillas con el rasgo dominante eran obtenidas aproximadamente tres veces más frecuentemente que las semillas con el rasgo recesivo.
En un segundo experimento, analizó las semillas generadas por las plantas crecidas desde semillas obtenidas en la primera generación y concluyó que
entre las plantas crecidas desde semillas de la primera generación con el carácter dominante, aquéllas que por autofecundación dieron lugar a semillas con el rasgo dominante o con el rasgo recesivo eran aproximadamente dos veces más que aquéllas que sólo daban lugar a semillas con el rasgo dominante.
Hasta este punto, poco parece haber sobre cadenas de Markov, ni tan siquiera probabilidades en nuestros comentarios sobre los trabajos de Johann Mendel, pero no nos dejemos engañar como ahora veremos.
Para hacer evidente la conexión entre la herencia de los caracteres fenotípicos y las cadenas de Markov, hacemos énfasis primero sobre los dos siguientes postulados hechos por Johann Mendel, donde aparece la noción de probabilidad:
- El carácter o rasgo (dominante o recesivo) de una semilla es la consecuencia de los factores ocultos, denotados por A (dominante) y a (recesivo), de manera que existen tres combinaciones posibles o factores AA, Aa y aa. Las semillas con las combinaciones AA y Aa tienen el rasgo A dominante, mientras que las semillas con la combinación aa tienen el rasgo a recesivo.
- Los granos de polen y los gametos transmiten sólo uno de los dos rasgos con idénticas oportunidades o probabilidades.
Como consecuencia, el cruce de dos linajes puros AA y aa conduce a híbridos con los factores Aa y el rasgo A dominante, mientras que los gametos de híbridos con los factores Aa transmiten el rasgo A con probabilidad ½ y el rasgo a con probabilidad ½.
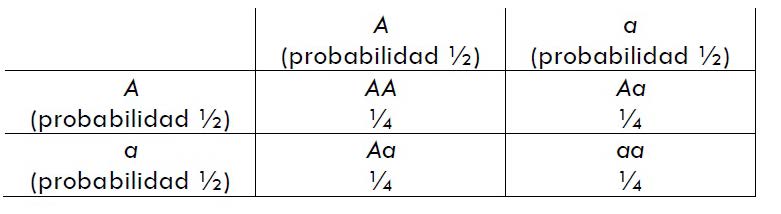
La siguiente tabla resume los posibles resultados del proceso de autofecundación de un híbrido Aa y sus probabilidades, en función de los rasgos A y a transmitidos por los gametos masculinos (fila) y femeninos (columna):
Es sencillo comprobar la propiedad Markoviana en la evolución de los factores AA, Aa y aa en las futuras generaciones. Por ejemplo, comenzando con N semillas híbridas Aa y asumiendo que cada planta da lugar por autofecundación sólo a 4 semillas, los números medios de semillas AA(n+1), Aa(n+1) y aa(n+1) en la generación n+1 pueden evaluarse desde los correspondientes números medios en la generación anterior n:
AA(n+1) = Aa(n) + 4 AA(n),
Aa(n+1) = 2 Aa(n),
aa(n+1) = Aa(n) + 4 aa(n).
En la terminología genética moderna, los rasgos son denominados alelos y los factores son llamados genotipos.
Las mejoras en las leyes de la herencia de Mendel
Los biólogos de la época, recelosos de los resultados de Johann Mendel, se preguntaban por qué el rasgo dominante no se hacía más frecuente de generación en generación. El genetista británico Reginald Punnett formuló esa pregunta a uno de sus compañeros de cricket en Cambridge, el matemático Godfrey Harold Hardy, quien publicó en 1908 el artículo titulado “Mendelian proportions in a mixed population” (“Proporciones Mendelianas en una población mezclada”) con una solución del problema bajo la hipótesis de que, en el caso de una población de tamaño infinito, la elección de la pareja sexual de un individuo sería aleatoria.
Godfrey Harold Hardy (Surrey, 1877 – Cambridge, 1947)
Al igual que Johann Mendel, Godfrey Harold Hardy centró su interés en una población diploide, es decir, con dos alelos, A y a, donde A es dominante y a es recesivo, y se interesó en determinar las frecuencias p(n), 2q(n) y r(n) de los genotipos AA, Aa y aa, respectivamente, en la generación n, con p(n)+2q(n)+r(n)=1. Para ello, asumió que ninguno de los genotipos incrementaba su mortalidad o decrecía su fertilidad en comparación con los otros dos genotipos. Las frecuencias en la generación n+1 pueden computarse desde las frecuencias en la generación n, observando que un individuo elegido aleatoriamente en la generación n transmite el alelo A con probabilidad p(n)+ q(n), bien porque el genotipo es AA y el alelo A se transmite con probabilidad 1, o porque el genotipo es Aa y el alelo A se transmite con probabilidad ½; de manera análoga, el alelo a se transmite con probabilidad q(n)+r(n).
El modelo resultante, conocido como ley de Hardy-Weinberg debido a que los resultados obtenidos por Godfrey Harold Hardy fueron también derivados ese mismo año 1908 por el médico alemán Wilhelm Weinberg (Stuttgart, 1862 – Tübingen, 1937), nos conduce a una actualización de la tabla de Johann Mendel para las frecuencias de los genotipos AA, Aa y aa en la generación n+1 en función de las frecuencias de los alelos A y a transmitidos por el padre (fila) y la madre (columna).
De nuevo, es posible observar la propiedad Markoviana en las expresiones de las frecuencias de los genotipos AA, Aa y aa en la generación n+1, que vienen dadas por
La ley de Hardy-Weinberg falla cuando se pretende capturar el fenómeno de la evolución genética en una población diploide finita, donde la tendencia aleatoria juega un papel relevante.
El modelo de Wright-Fisher
El estadístico y biólogo británico Ronald Aylmer Fisher y el genetista estadounidense Sewall Green Wright (Melrose, 1889 – Madison, 1969) serían los primeros en proponer un modelo matemático que incorporaba aleatoriedad en poblaciones diploides finitas sin mutación.
En el supuesto de una población diploide de tamaño N y genotipos AA, Aa y aa de los alelos A y a, el número Xn de alelos A en la generación n puede ser visto como una variable aleatoria – dado que el número total de alelos es 2N en cualquier generación, el número de alelos a en la generación n es 2N – Xn– y la sucesión de números {Xn : n ∈ {0, 1, … }} resulta ser una cadena de Markov en tiempo-discreto sobre el espacio de estados S = {0, 1, … , 2N } con probabilidades de transición en una etapa homogéneas en el tiempo
Esta expresión es obtenida teniendo en cuenta que los 2N alelos de la generación n+1 son obtenidos desde los 2N alelos de la generación anterior como si desarrollásemos 2N intentos independientes de Bernoulli, donde las respectivas probabilidades de obtener un alelo A (“éxito” en el intento de Bernoulli) y un alelo a (“fracaso”) son i/2N y (2N-i)/2N, en el supuesto Xn = i. Después de un número finito de generaciones, la población termina siendo homocigótica como consecuencia de que la absorción en alguno de los estados {0, 2N} es segura. En el contexto de la cadena de Markov, los estados 0 y 2N son absorbentes y equivalen a una población homocigótica de genotipos aa y AA, respectivamente, y son alcanzados en un número medio finito de generaciones.
Las probabilidades de fijación (absorción) en los alelos a (estado 0) y A (estado 2N) vienen dadas por
donde T = inf {n: Xn∈{0,2N}} equivale a la generación en la que, por primera vez, la población es homocigótica.
En el año 1922, Ronald Aylmer Fisher publicó el artículo titulado “On the dominance ratio” (“Sobre el cociente de dominancia”) donde combinó las leyes de Mendel y el principio de selección natural de la teoría de la evolución de Charles Darwin, explicando entonces las dos situaciones antagónicas de coexistencia de genotipos y de extinción de uno de los genotipos. Su modelo puede ser visto como una evolución del modelo de Godfrey Harold Hardy, donde se asume que los individuos con genotipos AA, Aa y aa tienen diferentes mortalidades antes de alcanzar la edad adulta.
Ronald Aylmer Fisher (Londres, 1890 – Adelaida, 1962)
Tomando p(n), 2q(n) y r(n) como las frecuencias de los genotipos AA, Aa y aa entre los individuos adultos de la generación n, las frecuencias de estos genotipos entre los individuos nacidos en la generación n+1 son (p(n)+q(n))2, 2(p(n)+q(n))(q(n)+r(n)) y (q(n)+r(n))2, de modo que las frecuencias de los genotipos entre los individuos adultos en la generación n+1 tienen la forma
donde s(n)=α(p(n)+q(n))2+2β(p(n)+q(n))(q(n)+r(n))+γ(q(n)+r(n))2, en el supuesto de que α, β y γ representen las probabilidades de que un individuo con los genotipos AA, Aa y aa, respectivamente, complete el proceso de maduración.
La ausencia de selección natural equivale a la elección α=β=γ y nos lleva a las ecuaciones escritas por Godfrey Harold Hardy.
La principal aportación de Ronald Aylmer Fisher se refiere a una expresión para el incremento entre las frecuencias alélicas de A sobre los individuos adultos de dos generaciones sucesivas, que le permitió observar que existen, al menos, dos estados estables donde las frecuencias alélicas del alelo A permanecen constantes: f = 0 (población homocigótica del genotipo aa); y f = 1 (población homocigótica del genotipo AA). Dicho de otra forma,
en una población diploide (con alelos A y a) infinita con apareamiento aleatorio sin mutación y selección natural,
(a) El alelo a desaparecerá progresivamente, en el supuesto de que el genotipo AA tenga mejores oportunidades selectivas para sobrevivir (es decir, α>β y α>γ).
(b) Los tres genotipos AA, Aa y aa podrán coexistir permanentemente en la población cuando el genotipo Aa tenga una ventaja selectiva sobre los genotipos AA y aa (es decir, β>α y β>γ).
En el año 1930, Ronald Aylmer Fisher publicaría el libro “The Genetical Theory of Natural Selection” (“La Teoría Genética de la Selección Natural”) con una amplia repercusión en la comunidad científica. Junto a Sewall Green Wright y el genetista y biólogo evolutivo británico John Burdon Sanderson Haldane (Oxford, 1892 – Bhubaneswar, 1964), Ronald Aylmer Fisher es hoy considerado uno de los fundadores de la Genética de Poblaciones como la corriente científica que concilia la metodología biométrica del matemático y estadístico británico Karl Pearson (Londres, 1857 – Surrey, 1936) con la Genética Mendeliana dirigida por William Bateson. Sin embargo, no hay que olvidar quién y cómo comenzó esta historia, con el monje Johann Mendel experimentando con guisantes en los jardines de su abadía.
Es el momento de concluir esta entrada, atípica por lo denso de sus contenidos, donde las matemáticas se mezclan con la genética. Más detalles matemáticos, todavía a nivel divulgativo, sobre este apasionante recorrido desde las leyes de la herencia de Johann Mendel hasta la actualidad pueden encontrarse en el capítulo 4 del libro Las Matemáticas de la Biología (Editorial Catarata, 2019). El lector ávido de detalles sobre el uso de cadenas de Markov, en particular, en Epidemiología quizá quiera contactar con los autores, quienes estarán encantados de compartir con él materiales sencillos sobre su investigación matemática.
_____
Manuel de León (Instituto de Ciencias Matemáticas CSIC, Real Academia de Ciencias) y Antonio Gómez Corral (Universidad Complutense de Madrid)