![]()
EuroGIGA: geometría, computación y matemática discreta en la base de la innovación tecnológica
Recogemos en Matemáticas y sus fronteras la noticia del próximo inicio de un programa europeo en el que grupos de investigadores de varios países, España entre ellos, van a cooperar de forma intensa y transversal en temas que se hallan en el corazón matemático del avance tecnológico.
El marco europeo del programa
A mediados de 2009 la European Science Foundation recibió 70 propuestas de programas de investigación para que se considerara su realización dentro de las iniciativas EuroCORES, un marco concebido para el desarrollo de investigaciones consideradas prioritarias y difícilmente abordables sin un amplio esfuerzo cooperativo internacional. Tras un extenso proceso de sucesivos arbitrajes por expertos y de valoraciones de financiación e impacto, en 2010 se seleccionaron 7 de las propuestas para que se llevaran a cabo, entre ellas EuroGIGA, la primera de carácter matemático en la historia de EuroCORES. La convocatoria de participación condujo a la formulación de varios proyectos específicos de investigación para el período 2011-2014, inscritos en EuroGIGA, cada uno integrado por equipos de diversos países europeos, en los cuales está prevista la intervención de dos equipos españoles coordinados por el el profesor Alberto Márquez (Universidad de Sevilla ) y el profesor Ferran Hurtado (Universidad Politécnica de Cataluña).
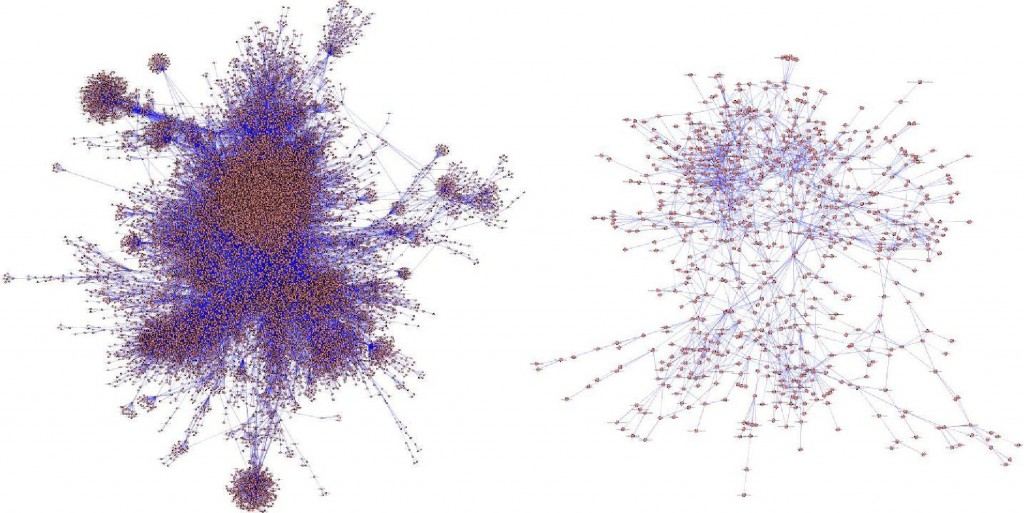
Una de las herramientas para el tratamiento de la información consiste en el uso de grandes grafos geométricos, con un número a menudo enorme de nodos-vértices que se conectan de acuerdo a un determinado significado.
La temática de EuroGIGA
El núcleo central del programa consiste en el estudio de diversos grafos e hipergrafos geométricos que se hallan en el corazón de la geometría discreta y computacional, y son a su vez herramientas básicas en numerosas aplicaciones tecnológicas en el campo de la informática y de las comunicaciones.
El tratamiento automático de la información (es decir, ¡la informática!) y la tecnología digital tienen primordialmente asociada una rama de las matemáticas, la matemática discreta, cuyos pilares básicos son la combinatoria y la teoría de grafos. La combinatoria estudia el recuento y enumeración de objetos, permitiendo estimar la complejidad de un objeto, algoritmo o estructura, y la generación y exploración de sus variantes. Los grafos son estructuras abstractas formadas por unos nodos o vértices, cada dos de los cuales se consideran conectados cuando cumplen cierta propiedad o relación. A menudo los nodos se representan como puntos del plano y las conexiones o aristas por segmentos o arcos de curva que los unen. Podemos imaginarnos un grafo en el que los nodos correspondan a empresas y las conexiones a las relaciones comerciales, otro en que los nodos estén asociados a servidores de internet y las aristas sean los vínculos directos entre ellos, o un tercero en que los vértices sean puntos del plano o del espacio cuyas coordenadas hayan sido capturadas por un cañón láser, unidos por aristas que constituyan una malla que permita representarlos.
La abstracta versatilidad de los grafos como estructura es lo que explica el gran espectro de aplicaciones en que se utilizan hoy en día; lo mismo que sucede -y no es causalidad- en informática, donde vemos, por ejemplo, como música, texto o imagen se trasladan a formatos únicos de codificación de la información. El estudio de los grafos contiene una disciplina matemática intrínseca pero inseparable de otras áreas de la matemática, como el álgebra, el análisis o la geometría.
Muchos grafos son por naturaleza geométricos, como las redes de transporte, las mallas que se utilizan para la representación gráfica de los objetos, o los grafos de proximidad que permiten analizar las nubes de puntos, pero hay muchísimos más, como es el caso de las estructuras moleculares, por ejemplo las proteínas, algunas de cuyas propiedades se estudian en términos de rigidez, plegado y acoplamiento, cuya formulación es claramente geométrica. Es uno de los campos de interacción entre la biología computacional y la geometría computacional.
La imagen de la izquierda es una malla toroidal: un grafo 4-regular trazable sobre el toro. La imagen de la derecha es la de una proteína, que se estudia desde el punto de vista cinemático y de rigidez.
La geometría computacional es una disciplina a caballo entre las matemáticas y la informática teórica. Su objetivo principal es el diseño y análisis de algoritmos para resolver eficazmente problemas geométricos, que típicamente involucran el manejo de datos masivos. Por consiguiente, una tarea fundamental es la identificación de conceptos, propiedades y técnicas que ayuden al descubrimiento e implementación de dichos algoritmos, lo que lleva al estudio de las estructuras de datos geométricos, la complejidad de los algoritmos, la representación y manipulación de figuras y de objetos, la construcción de lugares geométricos y, más en general, al desarrollo de los fundamentos matemáticos correspondientes. En particular, los problemas que se estudian incluyen la búsqueda y el recuento geométricos, la convexidad y sus generalizaciones, la proximidad, la intersección, descomposición y aproximación de formas y la visibilidad. Las áreas principales de aplicación son la informática gráfica, el diseño y fabricación asistidos por ordenador, el reconocimiento automático de formas, el diseño de grandes circuitos integrados, la visión artificial, los sistemas de información geográfica y la robótica.
Una de las características de muchos de los problemas de geometría computacional es la necesidad de manejar cantidades ingentes de datos, lo que hace que problemas aparentemente inocentes dejen de serlo. Por ejemplo, supongamos que nos dan 100.000 puntos del plano, descritos por sus coordenadas, y que necesitamos saber qué par de puntos de entre los dados está a distancia mínima. El problema parece que puede resolverse de manera muy sencilla: calcúlese la distancia entre cada par y tómese el mínimo valor obtenido. Sin embargo, esto es inviable en la práctica, porque hay aproximadamente diez mil millones de distancias que tendrían que ser calculadas. Si, por ejemplo, cada una se calcula en un una milésima de segundo, nos harían falta ¡unos cuatro meses de cálculos! Parece sorprendente, pero el estudio estructural y algorítmico del problema demuestra que basta con evaluar unas 300.000 de esas distancias «adecuadamente escogidas», con lo que, siguiendo con el ejemplo, bastan unos pocos segundos para realizar el cómputo completo. Las «distancias adecuadas» son, precisamente, las aristas de cierto grafo geométrico que se construye tomando los puntos dados como vértices.
La geometría computacional es inseparable de la geometría discreta y combinatoria, que estudia conjuntos discretos o finitos de objetos básicos, particularmente la complejidad combinatoria de los arreglos y de las estructuras que los describen: cómo se cortan, cómo descomponen el espacio, como se pueden formar recubrimientos, etcétera. Esta disciplina tiene también un solapamiento sustancial con otras bien establecidas, como la geometría convexa, o muy recientes, como la geometría digital. Aunque a menudo todas estas disciplinas se usan conjunta e inseparablemente en la resolución de un problema, hay algunos que permiten enfatizar el papel de cada una. Por ejemplo, consideremos un conjunto de n cuerpos convexos en en el espacio tridimensional. Si existe una recta orientada que los corta a todos, una 1-transversal, ésta induce un orden o permutación geométrica de los objetos. Cuántos de estos órdenes distintos pueden generar los mismos n objetos es un problema propio de la geometría combinatoria. Hallar condiciones necesarias y suficientes para que existan 1-transversales, lo es de la geometría discreta. Finalmente, dados n cuerpos específicos, hallar efectivamente sus 1-transversales, si es que existen, corresponde a la geometría computacional. Como el lector sin duda ya adivina, la capacidad de resolver cualquiera de estos problemas exige hacerlo en todas sus facetas.
Diagramas de Voronoi
Uno de los proyectos de EuroGIGA está centrado en el estudio de los diagramas de Voronoi. En el caso más sencillo, se tienen n puntos (o lugares) del plano y a cada uno de ellos se le asocia una región convexa, la región de Voronoi de ese lugar, de forma que los puntos del plano que están dentro de su región están más cerca del lugar que la define que de cualquiera de los restantes. De esta manera se obtiene un complejo celular que captura muy eficazmente la noción de proximidad y, en particular, es un potente modelo para simular el crecimiento competitivo de los organismos, o las áreas de influencia de tiendas y servicios, o calcular la ubicación óptima de cualquiera de ellos. La parte derecha de la figura adjunta muestra el diagrama de Voronoi de un conjunto de puntos no regular pero sí distribuidos con cierta uniformidad, evidenciando el carácter celular de un tejido que se ha formado por propagación simultánea desde unos núcleos iniciales. La figura de la izquierda muestra el diagrama generado por las capitales de provincia sobre un plano euclídeo ideal. Pese al carácter isotrópico del modelo usado, que ignora la influencia de la historia y la de la geografía, es notable la correlación que se observa con la realidad.
Los diagramas de Voronoi se pueden generalizar de muchas maneras, como cambiando el espacio ambiente, tomando otras métricas, o incluyendo obstáculos y zonas en que la propagación de la influencia tenga distintas velocidades. Esto permite una enorme flexibilidad en la modelización de fenómenos, que permite usarlos en áreas muy diversas, desde la arqueología a la zoología, pasando por la cristalografía, el estudio del voto político, los estudios de climatología, y la planificación de trayectorias sin colisión en robótica o de las de menor riesgo en cirugía asistida por ordenador.
Izquierda: Diagrama de Voronoi de las capitales de provincia (sobre un plano ideal dotado de la métrica euclídea). Derecha. diagrama de Voronoi de un conjunto numeroso de puntos.
Si conectamos los lugares que tienen regiones vecinas en un diagrama de Voronoi, se forma el grafo de Delaunay, que en el caso del plano es una triangulación. Este grafo tiene también muchas aplicaciones tecnológicas. Por ejemplo, es el que se usa en los modelos digitales del terreno, tanto en cartografía como en simuladores de vuelo y en juegos de ordenador y consola. También es la herramienta básica en la reconstrucción digital de superficies y sólidos a partir de datos que frecuentemente son puntos muestreados vía láser o secciones obtenidas tomográficamente.
Aunque se ha investigado mucho en estos temas, siguen surgiendo numerosos problemas además, aparte de que otros que siguen sin resolverse por completo. En EuroGIGA se estudiarán varios de ellos, como la complejidad y cálculo de los diagramas de puntos en movimiento, las generalizaciones de los diversos ejes esqueletales que se usan en el reconocimiento automático de formas, o las variantes de las triangulaciones y de los grafos de proximidad, que permiten el análisis de datos discretos espaciales dotándoles de estructura y forma, y permitiendo técnicas de discriminación o agrupamiento.
El tratamiento automático de la información geográfica (GIS) es una de las áreas de aplicación de los temas estudiados en EuroGIGA.
Geometría combinatoria y grafos geométricos
En los apartados anteriores hemos visto varias veces que los datos de partida son en muchas ocasiones conjuntos de puntos discretos, muy numerosos. Para poder analizarlos o desarrollar métodos eficaces que permitan agruparlos, conectarlos o simplificarlos, de cara a las diversas aplicaciones, es necesario entender con profundidad su estructura combinatoria. Imaginemos que trazamos 3 puntos distintos sobre el plano, ¿de cuántas maneras distintas puede hacerse? Si las distancias no son el aspecto más importante, podríamos decir que sólo hay dos maneras, o bien que formen un triángulo, o bien que estén alineados. De acuerdo; pues entonces ¿de cuántas maneras distintas se pueden disponer 7 puntos sobre el plano? ¿Y si son 70.000? Supongamos que estamos en este último caso, y que no hay tres de ellos alineados, ¿será cierto que siempre podremos encontrar una recta por dos de ellos que deje exactamente la mitad (34999) de los restantes a cada lado? Y si es así, ¿cuántas de esas rectas puede haber en un conjunto? La respuesta a la primera pregunta es que sí, que siempre se puede partir equilibradamente con una recta `por dos de los puntos … ¡pero la segunda pregunta es un problema que sigue abierto cuarenta años después de que fuera formulado!
Posiblemente el lector se pregunte qué sentido tiene un problema como el descrito, aparte de la curiosidad matemática. Lo cierto es que muchos algoritmos que han de procesar grandes cantidades de puntos empiezan por dividirlos en dos mitades mediante una recta, y luego procesan los dos subconjuntos de manera recursiva. El análisis completo del comportamiento de estos procedimientos está indisolublemente ligado a la comprensión combinatoria de estructuras como la bipartición que hemos explicado.
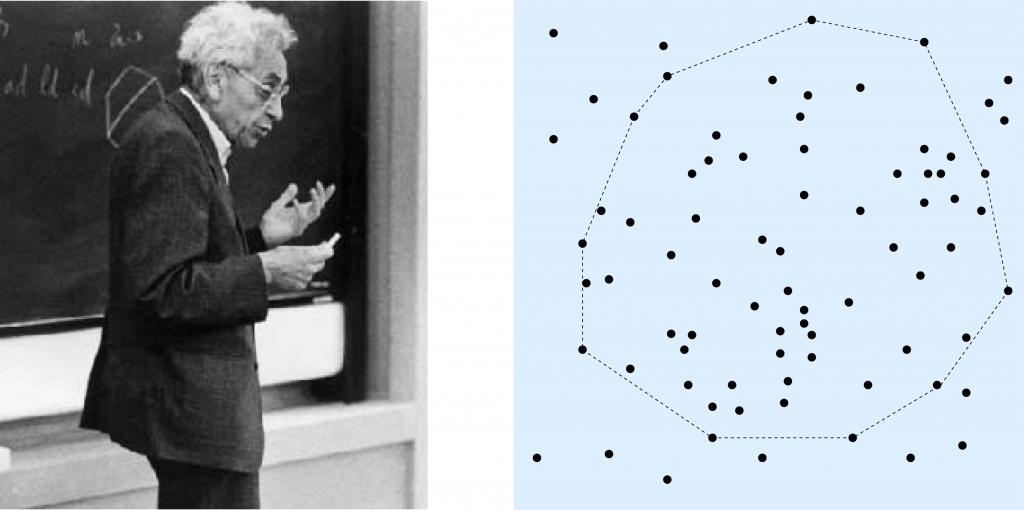
Hay muchos problemas en este campo que pueden formularse de manera muy sencilla y sin embargo ser extremadamente difíciles. Por ejemplo, puede decirse que cuando el número de puntos se hace muy grande, sea cual sea su posición, empiezan a aparecer subconjuntos en posición «bastante regular». En particular, y siendo más precisos, se puede demostrar que para cualquier valor entero n existe otro número f(n) tal que cualquier conjunto que conste de al menos f(n) puntos contiene un subconjunto de n puntos que constituyen los vértices de un polígono convexo (véase figura). Esto es lo que se llama el teorema de Erdős-Szekeres. Sin embargo, se desconoce el valor preciso de f(n), lo que se sabe es que, aproximadamente, 2^n ≤ f(n) ≤ 4^n, y estrechar el margen entre la cota inferior y la cota superior es un problema que lleva abierto muchos años.
El nombre del teorema anterior alude a dos investigadores húngaros, uno de los cuales, Paul Erdős, está considerado como uno de los más grandes matemáticos del siglo XX, y precisamente fue uno de los grandes estudiosos de la geometría combinatoria. Veamos otro problema que planteó él. Supongamos que tenemos dos conjuntos, cada uno con n puntos, y queremos saber si son exactamente el mismo, incluidas las distancias. Es decir, queremos decidir si el segundo conjunto se ha obtenido simplemente trasladando y girando el primero, de forma rígida que no altere las distancias entre cada dos puntos. El enfoque natural de cualquier algoritmo empieza por ver si ciertas distancias que se observan en el primer conjunto entre pares de puntos aparecen también en el segundo; o sea, buscando distancias repetidas.
Para ver si entendemos bien lo que estamos haciendo, podemos empezar por pensar, dado un único conjunto de n puntos, cuántas veces puede aparecer repetida una misma distancia. Por ejemplo, si n=3, podemos conseguir que una misma distancia aparezca tres veces, pues basta formar con los puntos un triángulo equilátero. Sin embargo, ¡de nuevo la respuesta exacta es desconocida para valores generales de n!
Uno de los proyectos de EuroGIGA se dedica especialmente a estudiar este tipo de problemas de geometría combinatoria, incluyendo varias extensiones del teorema de Erdős-Szekeres. Por otra parte, cuando los puntos de un conjunto finito se conectan mediante segmentos se obtiene un grafo geométrico, alguno de los cuales ya hemos mencionado, como las triangulaciones, y en el proyecto se estudiarán sus propiedades, su recuento, sus valores extremos, así como el diseño de algoritmos para la construcción de grafos óptimos según distintos criterios. También es un grafo geométrico el 1-esqueleto de un politopo, que es la envolvente convexa de un conjunto finito de puntos, y por supuesto los politopos son también un tema central de estudio dentro del proyecto. Un politopo puede definirse también por desigualdades lineales, lo que nos podría llevar a comentar el extensísimo campo de aplicaciones de la programación lineal. Remitimos al lector al artículo ya aparecido en este blog en el que se habló de este tema, con ocasión de la refutación de la conjetura de Hirsch por parte del profesor Francisco Santos, que es uno de los investigadores integrados en el equipo español de este proyecto dentro de EuroGIGA.
Uno de los máximos impulsores de la geometría combinatoria fue el matemático húngaro Paul Erdős (1913-1996). A la derecha, ilustración del teorema de Erdős-Szekeres
Conclusión
El tratamiento automático de información geométrica masiva está presente en la manipulación de imágenes digitales, desde los videojuegos a los métodos de diagnosis médica menos invasiva, pasando por la cirugía moderna, por los procesos industriales que incorporan control de calidad mediante visión artificial o diseño asistido por ordenador, o por los modelos de terrenos que permiten el tratamiento de la información geográfica o la simulación eficaz de fenómenos naturales.
Subyaciendo a toda esta tecnología que evoluciona muy rápidamente se ha generado la necesidad de dar respuesta matemática a muchos interrogantes nuevos. Sólo en el marco de proyectos cooperativos como EuroGIGA, combinando el esfuerzo de muchas instituciones e investigadores europeos, podemos esperar que se produzcan avances no sólo al ritmo de esa demanda, sino también anticipando y creando el futuro.
Nota. Agradecemos la cesión de diversas figuras: terreno triangulado (R. Silveira), proteína (I. Streinu), mapa de España (J. Cáceres), diagrama de Voronoi (K. Sugihara), malla toroidal (S. Kobourov). Los dos grandes grafos que aparecen en la primera figura están tomados del blog AI3 de M.Bergmann (http://www.mkbergman.com/date/2008/02/).
____________________________________________
Ferran Hurtado, Dept. de Matem. Aplicada II, Universitat Politècnica de Catalunya, Barcelona




[…] EuroGIGA: geometría, computación y matemática discreta en la base de la innovación tecnológica http://www.madrimasd.org/blogs/matematicas/2011/04/01/132682 por mezvan hace 2 segundos […]
[…] » noticia original […]
Este comentario es por mi curso propedeutico de la Escuela
[…] Matemáticas y sus fronteras – […]
[…] Matemáticas y sus fronteras – […]