La fascinación de los cristales de nieve

Especial Año Internacional de la Cristalografía (IYrC14)

Este año ha sido declarado como Año Internacional de la Cristalografía (IYrC14). Se conmemora el centenario de la difracción de rayos X como herramienta para el estudio de la materia cristalina, y también el 400 aniversario de la observación de simetría en los cristales de hielo (Kepler,1611), que dio comienzo al estudio profundo de la simetría en los materiales. En esta entrada, Manuel de León habla del trabajo del astrónomo y matemático aleman, Johannes Kepler.

Navidad de 1610, un hombre cruza el Puente de Carlos en Praga, nieva y los copos de nieve caen sobre la solapa de su abrigo. Es Johannes Kepler, pensando en qué regalo de Año Nuevo podría ser el más apropiado para su benefactor y amigo Johannes Matthäus Wäckher von Wackenfelds. Observa los copos de nieve, y en ellos encuentra una extraña regularidad. Como buen científico, no puede evitar preguntarse sobre ello:  ¿por qué todos tienen forma hexagonal?, ¿por qué no tienen cinco lados o siete?  Kepler piensa que este tema podría ser el motivo para un ensayo, un excelente regalo de Año Nuevo para su benefactor. Así escribe su obra «Strena seu de nive sexángula»  (El copo de nieve de seis ángulos), un librito de unas escasas 24 páginas que constituye, sin duda, una obra maestra.

En la introducción Kepler escribe a su amigo:

«Sí, sé bien que tan aficionado es usted a la nada; de seguro no tanto por su mínimo valor, sino por el juego divertido y delicioso que uno puede tener con ella, cual si fuera un gorrión feliz. Por tanto, me imagino que para usted un regalo debe ser mejor, y mejor recibido, cuando más se acerque a la nada”.

Kepler ironiza aquí con su situación en Praga, siempre pendiente de los pagos a destiempo y recortados de Rodolfo II, en cuya corte trabajaba Kepler de astrónomo, porque  ¿qué mejor regalo que dar nada para quién nada recibe? Por otra parte, Kepler hace un juego de palabras con nix (latín) que significa nieve, y nichts (alemán), que significa nada. Kepler piensa además que no habrá mejor regalo en esas fechas que reflexionar sobre algo que cae del cielo.

El astrónomo del rey

Kepler fue Praga en 1600 contratado por Tycho Brahe, el también astrónomo danés, considerado como el «mejor observador del cielo» antes del telescopio, gracias a los ingeniosos aparatos de medición que él mismo construída. Brahe, impresionado por los resultados teóricos de Kepler, estaba dispuesto a darle acceso a sus datos. De esta manera unieron esfuerzos dos personas con conocimientos complementarios – el observador de los cielos que aprovecha sus situación social privilegiada, con el estudioso de la teoría que anhela datos que corroboren sus intuiciones matemáticas -; las suyas fueron dos auténticas vidas paralelas que merecerían su Plutarco particular (en Praga puede contemplarse un monumento en las estatuas de ambos hombres, cada uno con los útiles de trabajo adecuados).

Además Kepler, un hombre errante en aquella Europa convulsionada por las guerras religiosas, había sido expulsado de Graz, Austria, donde había querido echar raíces, por su negativa a convertirse al catolicismo. Una vez en Praga, Kepler comienza su trabajo, que incluye el escribir un tratado en contra del archienemigo de Brahe, el también astrónomo Ursus. Inicia también una colaboración con Brahe para elaborar unas nuevas tablas astronómicas, las denominados posteriormente Tablas Rudolfinas, en honor de Rodolfo II, el emperador. En septiembre de 1601, Brahe muere repentinamente, y unos días después Kepler es nombrado astrónomo real en su sustitución.

Ser astrónomo real en aquella época era un buen empleo, pero exigía realizar trabajos astrológicos para el monarca, lo que no era muy de su gusto. Así y todo, esta época praguense es quizás la más pacífica en su agitada vida. Publicó mas de treinta trabajos, entre ellos la Astronomia Nova, y dos trabajos importantes de óptica, en uno de los cuáles sugirió el telescopio que hoy lleva su nombre. ¡Hasta tuvo la oportunidad de observar una supernova en octubre de 1604! Sin embargo, la muerte de Rodolfo II, las tensiones religiosas crecientes, la muerte de su esposa Barbara y de su hijo Friedrich de seis años, obligaron a Kepler a trasladarse de nuevo, esta vez a Linz, Austria.

¿Por qué la forma hexagonal?

En el ambiente de tranquilidad praguense es cuando Kepler escribe «Strena seu de nive sexángula». El análisis de Kepler es profundo, y deduce que la forma particular de los copos de nieve debe ser consecuencia de la manera en la que se empaquetan las partículas que los constituyen. Kepler unifica así dos conceptos: el mundo geométricamente ordenado y creado por un Dios matemático, con una ciencia que trata de explicar los fenómenos naturales buscando las causas y leyes que los producen.

Se puede pensar en esas partículas como glóbulos, que se apilan ocupando el mínimo espacio posible, y el empaquetamiento hexagonal es el mejor. Basta ver las colmenas de las abejas, o las teselaciones de un plano, que pueden ser de triángulos, cuadrados o hexágonos.

En éste mismo ensayo, Kepler planteó su famosa conjetura de empaquetamiento, resuelta 300 años despues por Thomas Hales. Años antes, Kepler había compartido correspondencia con el astrónomo y matemático inglés Thomas Harriot, acerca de la manera óptima de apilar balas de cañón en la cubierta de un buque. Sir Walter Raleigh, de quién Harriot fue ayudante, le había planteado la cuestión  cuando estaban planificando una expedición en 1585 rumbo a Virginia, a fin de establecer allí la primera colonia británica.

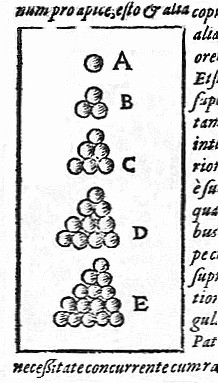
La conjetura de Kepler establece que la mejor manera es la que usan los fruteros para las naranjas, poniendo cada naranja de la siguiente capa apoyada en el hueco de las cuatro naranjas que estrán justo debajo en la primera capa. Este método minimiza el espacio dejado por los huecos entre las naranjas.

Durante siglos, trataron de demostrarla numerosos matemáticos como Gauss, que la probó en el caso regular. En el Congreso Internacional de Matemáticos de 1900, fue incluida por David Hilbert entre su lista de los 23 problemas más importantes para el siglo XX (el problema número 18). Pero el asunto no tuvo mayores avances hasta que el matemático húngaro Laszlo Fejes Toth redujo el problema a un número finito pero enorme de cálculos. Thomas Hales fue capaz de realizar las cuentas en los años 90, ayudado por la potencia del ordenador. El resultando se publicó en Annals of Mathematics, y con ello la conjetura quedó resuelta. Aunque todavía hoy en día no todos los matemáticos aceptan que esto pueda considerarse una auténtica prueba.

Lo que hoy sabemos de la nieve

Kepler no tenía el conocimiento actual de cómo está constituida la materia. No sabía que una molécula de agua está formada por dos átomos de hidrógeno y uno de oxígeno, formando un ángulo de 104,5 grados. Estas moléculas de agua están ligadas con enlaces con sus vecinas, formando tetraedros. Cuando la temperatura baja, se acercan más entre sí y forman esas estructuras de seis lados.

Si esta explicación no resulta satisfactoria, y queremos una más poética, se puede recurrir a la lectura del precioso relato The Queen of the Rain Was in Love with the Prince of the Sky, escrito por Eugene Mirabelli; que también muestra por qué dos copos de nieve nunca son iguales.

—

Manuel de León (CSIC, Real Academia de Ciencias y Academia Canaria de Ciencias) es Director del Instituto de Ciencias Matemáticas (ICMAT) y vocal del Comité Ejecutivo de IMU.

Ágata A. Timón es responsable de Comunicación y Divulgación del ICMAT.