![]()
Instrumentos musicales, animales y las matemáticas
Seguimos en esta nueva entrada hablando de música y matemáticas, hoy con los instrumentos musicales.
Las familias de instrumentos se dividen en tres clases: cuerda, viento y percusión. A su vez, cada una de estas familias se divide en subfamilias: arco, arpa y piano para la primera, madera y metal para la segunda y parches e idiófonos para la última. La característica común de todos estos instrumentos tan distintos en principio, es que su sonido enmascara una ley física y, consecuentemente, una ley matemática.
[youtube]https://www.youtube.com/watch?v=MJvj9C_n1rc&index=12&list=PL55D459D961D83B80[/youtube]
Los Straitjackets – «Yeah Yeah Yeah»
Ya hemos comentado el monocordio de Pitágoras, y es evidente que éste supuso el preludio de los instrumentos de cuerda. El mecanismo de una guitarra es el mismo monocordio multiplicado por seis. También lo es en el caso del piano, cuyo mecanismo, aunque más escondido, también se corresponde con el de la cuerda pulsada.
Para entender el mecanismo de los instrumentos, necesitamos utilizar la física de las ondas. La física de ondas es una materia de estudio desde hace siglos; de hecho, todos hemos disfrutado en nuestra niñez de nuestro primer experimento con la física de ondas: lanzar una piedra al agua y observar la propagación del agua circundante en forma de frente de onda con simetría esférica.
En 1834, John Scott Russell observó por primera vez un caso particular de onda, los denominados solitones. El fenómeno observado por este ingeniero escocés, fue la propagación de una onda surgida en las aguas de un canal como estela de la pieza arrastrada por dos caballos uncidos al yugo.
El solitón se definió en aquel momento como una onda imperturbable, muy localizada, que remontaba su altura y velocidad a pesar de la corriente. Desde entonces, las propiedades de scattering de estas ondas y su presencia en múltiples fenómenos físicos (principalmente a altas energías en las que se ponen de manifiesto los efectos no lineales) son un tema de enorme interés.
Sin embargo, la física de ondas subyacente a los instrumentos es más sencilla que la de los denominados solitones. Para poder entenderlo, conviene revisar cómo se produce el sonido.
De forma muy simplificada, podemos definir la música como un conjunto de sonidos armoniosos que deleitan nuestro sentido auditivo. También de forma muy simplificada, diremos que el sonido es un conjunto de ondas sonoras. Si seguimos concatenando definiciones simplificadas, a su vez las ondas sonoras son un conjunto de vibraciones que alteran el aire en que se propagan, produciendo cambios de presión, que constituyen las ondas sonoras.
Las ondas de sonido son longitudinales, quiere decir que su dirección de vibración y desplazamiento son la misma. Existen ondas transversales, en las que la dirección de desplazamiento de la onda es perpendicular a la dirección de vibración. Este es el caso del ejemplo descrito para las ondas esféricas provocadas al tirar una piedra en un estanque.
Las ondas longitudinales vienen descritas por su longitud de onda que se define como la distancia entre dos crestas o vientres o la distancia entre dos nodos. Se representa mediante la letra griega lambda. En otras palabras, la longitud de onda es distancia entre dos puntos consecutivos de máxima vibración o de mínima, respectivamente. La inversa de la longitud de onda se denomina frecuencia, y así puede entenderse como el número de repeticiones por unidad de tiempo. Se mide en Hertzs en el SI, en honor al físico alemán, premio Nobel en 1925 por sus aportaciones al estudio de la corriente eléctrica.
El tono de nuestro sonido musical se identifica con la frecuencia. Decimos que nuestro sonido es grave si las vibraciones son de baja frecuencia y decimos que sonamos agudo si emitimos vibraciones de alta frecuencia. En el caso de que nuestra frecuencia sonora se duplique, decimos que estamos una octava por encima. El oído humano es capaz de identificar un rango de diez octavas en la escala de frecuencias sonoras, pero muchos animales superan con creces nuestras posibilidades. Por ejemplo, los murciélagos emiten sonidos, cuya onda rebotada contra el entorno, es interpretada por sus sistemas nerviosos. Los delfines proceden de manera similar, lanzando chillidos que rebotan en sus mandíbulas, con lo que consiguen una idea clara de cómo es su entorno.
Los elefantes tienen un oído más agudizado que el humano, siendo capaces de detectar frecuencias veinte veces inferiores a nuestro rango auditivo. Este hecho se debe al fenómeno de propagación de ondas sonoras a través de sus patas y trompas. Las palomas, también son capaces de detectar frecuencias tan bajas que hacen de su sentido de la orientación un paradigma.
El volumen de nuestra música está relacionado con la amplitud de las ondas de sonido. Definimos la amplitud de la onda como la distancia entre el eje de las X y la altura máxima de vibración de la onda.
Sin embargo, nuestra forma de percepción del volumen acústico no es lineal. La escala es logarítmica y sigue la siguiente ecuación matemática.
L= 10 log10 I/I0
donde I es la potencia a estudiar en vatios, I0 es un valor de referencia igual a 10-12 v/m2 (vatios por metro cuadrado) y el logaritmo es el logaritmo en base diez.
El cálculo resultante mide la sensación de un oyente. Es una cantidad de potencia y se mide en decibelios. Un decibelio es la décima parte de un belio, que es el logaritmo de la relación entre la cantidad estudiada y la de referencia. A efectos prácticos, es más cómodo el uso de los decibelios. El nombre belio se acuñó en honor al científico escocés Graham Bell.
El timbre depende de la forma de la onda sonora. Los instrumentos, debido a su construcción y forma, impondrán condiciones de contorno sobre nuestra onda. De ahí que surjan diferentes sonidos, basados en la topología del instrumento.
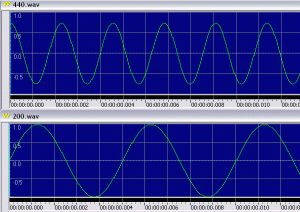
En general, las ondas generadas por los instrumentos son de carácter sinusoidal, es decir, su ecuación descriptiva fundamental es una función seno. Las combinaciones de conjuntos de sinusoides, componen la melodía. A la frecuencia más baja se la denomina frecuencia fundamental, por consiguiente, aquella con longitud de onda mayor (equivalente a no pulsar en ningún punto intermedio la cuerda de una guitarra, por ejemplo). A las frecuencias más altas, correspondientes a longitudes de onda menores, se les denomina armónicos. La generación de armónicos es comparable a pulsar una cuerda en un número determinado de puntos, es decir, dar lugar a la “creación de nodos” o puntos de mínima vibración por efecto de la presión ejercida (con los dedos en los trastes).
En el caso de los instrumentos de viento, la creación de estos nodos es directa, dependiendo del número de orificios que tapemos en una flauta y su disposición conveniente.
De esta manera, la propagación y características de las ondas sonoras son equivalentes en las tres familias de instrumentos, salvo que su forma de fabricación y materiales influyen en el resultado, pero la misma noción física es aplicable a todos ellos.
En el caso del tambor, la onda se propaga en la superficie construida por una membrana denominada parche. Las ondas creadas son tan sensibles que dependen del material del parche y de su grosor, afectando a los armónicos producidos. Por ejemplo, en el caso del jazz se utilizan parches texturizados, o parches con un material adicional que ejerce un efecto de fricción en las escobillas.
La geometría del instrumento también es crucial. En el caso de un tambor con simetría esférica, las ondas tienden a propagarse adecuándose a la forma del instrumento. El sonido resultante será en parte dependiente no sólo de la geometría circular de la membrana, sino también del cilindro que actúa como caja de resonancia del tambor y además de sus bordes. Por todas estas razones, podemos decir que “podemos oír la forma de un tambor”.
—
Manuel de León (CSIC, Fundador del ICMAT, Real Academia de Ciencias, Real Academia Canaria de Ciencias, ICSU) y Cristina Sardón (ICMAT-CSIC).


[…] http://www.madrimasd.org/blogs/matematicas/2016/06/26/141747#403558 Comparte:TwitterFacebookGoogleMe gusta:Me gusta Cargando… Publicado en: Sin categoría […]
Un artículo muy interesante
The Best Apps and Games For Android ·https://clickmodapk.com/la-deportes-apk/