![]()
Lecciones aprendidas en Heidelberg
El pasado 24 de septiembre, la comunidad matemática estaba revolucionada ante el anuncio de que Sir Michael Atiyah presentaría en el Heidelberg Laureate Forum una demostración sencilla de uno de los santos Griales de nuestra disciplina, la hipótesis de Riemann.
Esencialmente, la hipótesis de Rieman nos dice que los ceros no triviales de la función zeta de Riemann tienen todos parte entera ½:
La función zeta de Riemann posee una intrigante conexión con la densidad de números primos, de ahí su gran interés.
Esta imagen tan espectacular de la función zeta fue construida por David Martín de Diego (más detalles en esta entrada de Matemáticas y sus fronteras):
Escribí un artículo sobre el anuncio de Atiyah, publicado el 25 de septiembre en El Mundo, Un alarde de erudición para ‘resolver’ la hipótesis de Riemann que acompañaba a otro de Miguel G. Corral, titulado Anuncian la solución de la hipótesis de Riemann, el enigma matemático que podría revolucionar internet.
No fueron los únicos artículos publicados en medios de comunicación, porque el anuncio estaba hecho por una persona del carisma y la categoría científica del Michael Atiyah, ganador de una medalla Fields en 1966 y del Premio Abel en 2004. Y estamos citando solo las dos más altas distinciones. Si hubiera sido el anuncio de otro matemático (y ha habido unos cuantos anuncios fallidos de la resolución de este problema) nadie le hubiera prestado mucha atención y la respuesta habría sido que no lo había probado.
Atiyah basó su prueba en las propiedades de la función de Todd, y la despachó en muy pocas líneas. No hubo muchos detalles, y los analistas tienen muchas dudas de que exista una función con las propiedades que se le adjudican. El argumento no convenció. Pero la gente no prestó atención a las obras que referenciaba en su anuncio: la de John von Neumann titulada On an algebraic generalization of the quantum mechanical formalism, esencial para la formulación matemática de la mecánica cuántica; una segundo titulada Arithmetic genera and the Theorem of Riemann-Roch, clásico en geomería algebraica, escrito por el matemático alemán Hirzebruch, y cuyo resultado principal está basado en la teoría del cobordismo de René Thom; y otra obra clásica del premio Nobel P.A.M. Dirac, The Quantum Theory of the Electron, en el que introduce la ecuación de onda del electrón unificando la mecánica cuántica y la relatividad especial.
Con estas tres pistas, Atiyah ya nos estaba dando una lección. Hay que seguir leyendo a los clásicos, hay que conectar las matemáticas con la física y el mundo real. Hablaremos en próximas entradas de algunas de estas maravillas que estaban detrás de las ideas de Atiyah para Heidelberg.

La segunda lección que hemos aprendido del Foro de Heidelberg es sobre la edad. Hemos visto en redes sociales algunos comentarios sobre la edad de Atiyah (89 años) y veladas alusiones a su capacidad intelectual. Publicamos hace tiempo una entrada sobre ese mito de la juventud que se ha instalado en las matemáticas, probablemente influenciado por la edad exigida para conseguir una medalla Fields. Atiyah ha dado otra lección, mostrando como a su edad se puede seguir manteniendo la ilusión, las ganas de buscar la verdad matemática allá donde se encuentre. Ojalá todos los matemáticos jóvenes mostraran esa vitalidad.
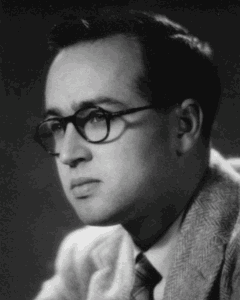
Es muy probable que la Fundación Clay no tenga que emplear ese millón de dólares, pero Sir Michael Atiyah ya tiene un lugar bien ganado en el Olimpo Matemático y de ahí no lo vamos a bajar nunca.
___
Manuel de León (CSIC, Fundador del ICMAT, Real Academia de Ciencias, Real Academia Canaria de Ciencias).

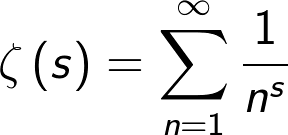

[…] El pasado 24 de septiembre, la comunidad matemática estaba revolucionada ante el anuncio de que Sir Michael Atiyah presentaría en el Heidelberg Laureate Forum una demostración sencilla de uno de los santos Griales de nuestra disciplina, la hipótesis de Riemann. Esencialmente, la hipótesis de Rieman nos dice que los ceros no triviales de la función zeta de Riemann tienen todos parte entera ½: La función zeta de Riemann posee una intrigante conexión con la densidad de números primos, de ahí su gran interés. Esta imagen tan espectacular de la función zeta fue construida por David Martín de Diego (más detalles en esta entrada de Matemáticas y sus fronteras): Escribí un artículo sobre el anuncio de Atiyah, publicado el 25 de septiembre en El Mundo, Un alarde de erudición para 'resolver' la hipótesis de Riemann que acompañaba a otro de Miguel G. Corral, titulado Anuncian la solución de la hipótesis de Riemann, el enigma matemático que podría revolucionar internet. No fueron los únicos […]
You need too take part in a contest for onne of the most useful blogs on the internet.
I’m going to highly recommend this blog!