![]()
¿Ha probado Athanassios Fokas la hipótesis de Lindelöf?
El matemático Athanassios Fokas, ha anunciado en un preprint en arxiv la solución a un antiguo problema matemático, la llamada Hipótesis de Lindelöf.

Fokas está considerado como uno de los matemáticos griegos más importantes, aunque a los 18 años marchó al Reino Unido para estudiar Aeronáutica en el Imperial College en Londres. Su gran amor eran sin embargo las matemáticas, así que hizo su tesis doctoral en este campo en Caltech en 1979. No acabaron ahí sus inquietudes disciplinares, así que también estudió Medicina en la Universidad de Miami, obteniendo su título en 1986.
Desde entonces, ha sido profesor en la Universidad de Clarkson, luego en el Imperial College y finalmente en Universidad de Cambridge.
Fokas ha desarrollado un intenso trabajo de investigación en muchas áreas, especialmente en las ecuaciones en derivadas parciales, con numerosas aplicaciones a la medicina (modelos matemáticos para la leucemia y el plegamiento de proteínas) pero también en relatividad. Es muy famoso el llamado método de Fokas para resolver problemas con frontera, y que se consierda el desarrollo más importante en el tema tras la transformada de Fourier.
Esta diversidad de intereses llevó a Israel M. Gelfand, a decir de Fokas que era un estilo de científico más propio del Renacimiento que de nuetsros días.
El año pasado, Fokas subió un preprint a arxiv en el que afirmaba haber probado la Hipótesis de Lindelöf. No parece que haya consenso sobre el tema, y Fokas ha ido modificando varias veces el preprint sin asegurar ahora que ha probado el resultado; de hecho, la última versión, la cuarta, se titula: A novel approach to the Lindelöf hypothesis.
Este tema resulta interesante porque muestra las dificultades en que un resultado relevante sea aceptado por la comunidad matemáticas, porque ha de pasar muchas “pruebas del algodón”. Incluso un matemático del prestigio de Fokas debe someterse a este escrutinio. Y esta es una de la sgrandes fortalezas de las matemáticas.
Pero es también una buena ocasión para contar en que consiste la Hipótesis de Lindelöf y el porqué de su relevancia.

Ernst Leonard Lindelöf fue un matemático finlandés, dedicado a la topología, quien formuló en 1908 su conjetura sobre el crecimiento de la función zeta de Riemann. Esta hipótesis tenía importantes consecuencias sobre uno de los problemas más relevantes de la matemática actual desde su formulación en el siglo XIX, la llamada hipótesis de Riemann. La relación es que la hipótesis de Riemann implica de la de Lindelöf, de ahí la relevancia de esta hipótesis.
La hipótesis de Riemann está a su vez relacionada con la distribución de los números primos. Estos pueden ir siendo calculados: 2, 3, 5, 7, 11, 13, etc., pero nos gustaría saber como se distribuyen a medida que vamos avanzando. De una manera misteriosa, esta distribución está asociada a los ceros de la función zeta, y en particular, a los llamados ceros no triviales, que según la hipótesis de Riemann están todos en la recta del plano complejo con valor real ½.
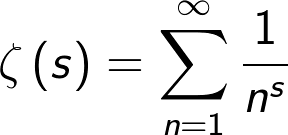
Probar la Hipótesis de Riemann, uno de los Problemas del Milenio, conlleva un premio de un millón de dólares por parte de la Fundación Clay. No sabemos todavía si Fokas ha conseguido iniciar una línea que pueda conducir a esta meta. El tiempo lo dirá.
____
Manuel de León (CSIC, Fundador del ICMAT, Real Academia de Ciencias, Real Academia Canaria de Ciencias, ICSU).

