![]()
¡No diga backgammon, diga Matemáticas!
Una de mis últimas lecturas ha sido la última novela de Jonathan Lethen, titulada “Anatomía de un jugador”. Lethen no es un cualquiera, ha sido Premio Nacional de la Crítica en 1999 en Estados Unidos por su obra “Huérfanos de Brroklyn”. “Anatomía de un jugador” es la historia de Alexander Bruno, un jugador, pero un jugador de backgammon. Va de un lado a otro, con su estuche de backgammon y la funda del esmoquin, dispuesto a jugar sus partidas con gente de dinero dispuestos a apostar grandes sumas. Su habilidad le sirve para que pueda darse una vida lujosa. Un día pasan cosas y aquí me detengo porque no le voy a fastidiar la trama a ningún lector.
Mi interés matemático por la novela se despierta por el juego en sí, el backgammon, que es un auténtico protagonista en la historia. No es un juego tan popular como el ajedrez, y mezcla el azar con la estrategia. La pregunta que me hice fue, ¿cúanto hay de azar y cuánto de estrategia?
En primer lugar, digamos que es un juego muy antiguo, que se emonta a la antigua Babilonia y a unos 5000 años de existencia. De hecho, se le considera el juego de tablero más antiguo del mundo. Se encontró una mesa de juego durante unas excavaciones arqueológicas en la ciudad de Shahr-i Sokhta, en el actual Irán. El juego se conoce en España con nombres como tablas reales, chaquete o chanchullo.
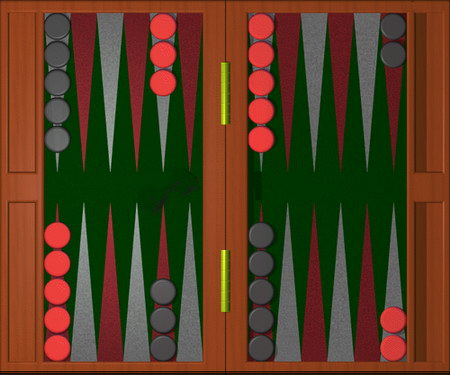
Describamos brevemente el juego (remitimos a esta página web para más detalles) . El backgammon consiste en un tablero dividido en cuatro partes de seis regiones triangulares sobre las que se colocan las piezas o fichas. Los jugadores son dos, y las fichas son de dos colores diferentes, por ejemplo, blancas y marrones, o rojas y negras. Las fichas se colocan en una posición inicial tal y como puede verse en la figura:
Se van tirando dos dados simultáneamente, y las fichas se pueden mover (unas en el sentido de las agujas de un reloj, las otras en el sentido contrario) de acuerdo con los resultados de las tiradas (una de las gracias del juego y que permite acciones estratégicas es que se pueden mover dos fichas según el resultado en cada dado, o una con la suma de ambos dados).
El juego comienza con una tirada de dados para decidir quién comienza el juego, que será el que obtenga mayor puntuación. En este caso, se tira uno solo de los dados y se comienza ya (según el orden) a mover las fichas. Posteriormente, el jugador que tiene el turno tira los dados y mueve las fichas según hemos indicado antes. Hay que recordar que una ficha no se puede mover a una posición bloqueada, es decir, donde se encuentran dos o más fichas contrarias. Si sólo existe una ficha contraria, la ficha es «capturada» y se coloca en la barra vertical (veáse la figura). Otra regla importante es que si el rtival captura una de tus fichas, tienes la obligación de volverla a introducir en cuanto puedas (si no se puede, se perdería el turno de jugada).
Otra característica interesante del backgammon es la doblada. Cuando un jugador en el momento de lanzar consigue un doble (los dos dados con el mismo valor), debe duplicar a su vez el movimiento, es decir, debe realizar cuatro movimientos por el valor que hubiera salido en los dados.
En el backgammon, los jugadores suelen pactar previamente un número de puntos, y vencerá el jugador que antes los alcance. Así que habitualmente son varias las partidas que se juegan. A lo largo de un juego, antes de tirar sus dados, cada jugador tiene la opción de ofrecer doblar la apuesta al contrario. Si en un momento dado un jugador ofrece una apuesta y el contrario no acepta, el que ha realizado la apuesta gana lo apostado hasta entonces y el juego se da por finalizado. El jugador que acepta la apuesta podrá volver a doblarla posteriormente; este mecanismo de doblar la apuesta ambos jugadores alternativamente puede repetirse sucesivas veces. Cuando el jugador que vence un juego queda a un solo punto de ganar la partida, durante el siguiente juego no será posible doblar la apuesta.
Si un jugador consigue sacar todas sus piezas del tablero antes de que el contrario haya conseguido siquiera sacar una sola, el juego es declarado doble o gammon, lo que implica que el valor de lo apostado será computado doble. Si además de no sacar ninguna pieza el contrario todavía tiene alguna de sus piezas capturada o en el primero de los cuadrantes del recorrido, el juego se considera backgammon, y en este caso la apuesta computa el triple.
En su novela, Lethem hace un guiño a la doblada, así que los capítulos se numeran como sigue: Uno, Dos, Cuatro, Ocho, Dieciséis, Treinta y dos, Sesenta y cuatro, Gammon y Backgammon. Y cada uno cuenta con cuatro partes.
Si no ha quedado muy clara la dinámica del juego, este video ayudará mucho (y hay muchos más circulando por la red):
[youtube]https://www.youtube.com/watch?v=7yiGkCFp-Ho[/youtube]
Una de las características de nuestro mundo es que en cualquier tema que te llame la atención, encontrarás multitud de personas que ya han pasado por allí. Así que tras una búsqueda en internet, encontramos libros como este, “The Mathematical Theory Behind Backgammon”, de Ali Khayat,
o este otro, “Luck, Logic, and White Lies: The Mathematics of Games”, de Jörg Bewersdorff, con su capítulo “»Backgammon: To Double or Not to Double»
así como una buena cantidad de artículos en los que se tratan desde diferentes puntos de vista las matemáticas que rigen la dinámica del juego. La teoría de probabilidades es una de las cuestiones a tener en cuenta, ya que conocer las probabilidades de sacar un número, bien en uno de los dados o con la suma, será de gran ayuda.
Esa combinación de azar y estrategia ha llevado también a un interés de los investigadores en las ciencias de la computación, y hoy en día, se ha desarrollado software como el TD-Gammon de IBM, con potencia suficiente para derrotar a jugadores humanos.
En su artículo “It’s All About Math—How I Learned This the Hard Way!”, Phil Simborg cuenta como llegó a la conclusión de que para ser un buen jugador de backgammon, hay que aplicar las matemáticas. Su resumen es aplastante:
Backgammon is Math. If you want to improve your game, work on the math. It’s that simple.
Y es que el backgammon reúne muchos elementos de las matemáticas: Lógica, Combinatoria y Probabilidades. ¡Qué más podíamos pedir! Si están interesados en saber más desde el punto matemático, este es uno de los numerosos artículos que se publican sobre el tema “Estimating Winning Probabilities in Backgammon Races”.
Confieso que hace muchos años jugué al backgammon, no muchas partidas. No recuerdo si ganaba o no, pero en caso de pérdida siempre nos quedará el consuelo de la sabiduría de los jugadores de backgammon que nos recuerda Ali Khayat: “Si pierdes en el backgammon, ganarás en el amor”.
Les dejo con una partida completa de backgammon, y les animo a practicarlo (trataré de seguir mi propio consejo):
[youtube]https://www.youtube.com/watch?v=qpiwSFMLCV4[/youtube]
___
Manuel de León (CSIC, Fundador del ICMAT, Real Academia de Ciencias, Real Academia Canaria de Ciencias).




Saludos. Cuantas veces se pueden tirar los dados para ingresar una ficha capturada de nuevo al tablero, y si hay mas de una capturada con la tirada de un par con los dados esto le da ingreso de nuevo al tablero a las dos fichas o solo a una ?????
Manuel muchas gracias por tu artículo, las entradas que propones son muy buenas
Hasta otro momento
Buscando estrategias para ajedrez en Google aterrizé aquí y me pareció más que interesante. Nunca juegué backgammon. Habrá que aprender. ¡Muy bueno el artículo!