Empaquetando esferas
En su ensayo Strena seu de nive sexángula (El copo de nieve de seis ángulos), Johannes Kepler planteó su famosa conjetura de empaquetamiento, resuelta 300 años después por Thomas Hales. Años antes, Kepler había compartido correspondencia con el astrónomo y matemático inglés Thomas Harriot acerca de la manera óptima de apilar balas de cañón en la cubierta de un buque. Sir Walter Raleigh, de quién Harriot fue ayudante, le había planteado la cuestión cuando estaban planificando una expedición en 1585 rumbo a Virginia, a fin de establecer allí la primera colonia británica.
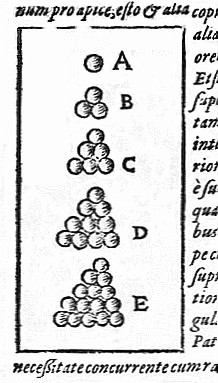
La conjetura de Kepler establece que la mejor manera es la que usan los fruteros para las naranjas, poniendo cada naranja de la siguiente capa apoyada en el hueco de las cuatro naranjas que están justo debajo en la primera capa. Este método minimiza el espacio dejado por los huecos entre las naranjas.
En geometría, un empaquetamiento esférico es una disposición de esferas que no se superponen dentro de un espacio contenedor. Las esferas consideradas suelen ser todas de idéntico tamaño, y el espacio suele ser un espacio euclídeo tridimensional. Sin embargo, los problemas de empaquetamiento de esferas pueden generalizarse para considerar esferas desiguales, espacios de otras dimensiones (donde el problema se convierte en empaquetamiento de círculos en dos dimensiones, o empaquetamiento de hiperesferas en dimensiones superiores) o espacios no euclidianos, como el espacio hiperbólico.
Un problema típico de empaquetamiento de esferas consiste en encontrar una disposición en la que las esferas ocupen la mayor parte posible del espacio. La proporción de espacio ocupado por las esferas se denomina densidad de empaquetamiento de la disposición. Dado que la densidad local de un empaquetamiento en un espacio infinito puede variar en función del volumen sobre el que se mide, el problema suele consistir en maximizar la densidad media o asintótica, medida sobre un volumen suficientemente grande.
Kepler no tenía una prueba de la conjetura, y el siguiente paso lo dio Carl Friedrich Gauss (1831), quien demostró que la conjetura de Kepler es cierta si las esferas se colocan en una red regular. Esto significaba que cualquier disposición de empaquetamiento que refutara la conjetura de Kepler tendría que ser irregular. Pero eliminar todas las disposiciones irregulares posibles es muy difícil, y esto es lo que hacía que la conjetura de Kepler fuera tan difícil de demostrar. Después de Gauss, no se hicieron más progresos para demostrar la conjetura de Kepler en el siglo XIX. En 1900, David Hilbert la incluyó en su lista de veintitrés problemas matemáticos sin resolver, formando parte del decimoctavo problema de Hilbert.
El siguiente paso hacia una solución lo dio László Fejes Tóth, quién, en 1953, demostró que el problema de determinar la densidad máxima de todas las disposiciones (regulares e irregulares) podía reducirse a un número finito (pero muy grande) de cálculos. Esto significaba que, en principio, era posible una prueba por agotamiento. Como se dio cuenta Fejes Tóth, un ordenador lo suficientemente rápido podría convertir este resultado teórico en un enfoque práctico del problema.
En 1990, Wu-Yi Hsiang afirmó haber demostrado la conjetura de Kepler. La demostración fue elogiada por la Encyclopædia Britannica y Science, y Hsiang también fue homenajeado en las reuniones conjuntas de la AMS-MAA. Wu-Yi Hsiang afirmó haber demostrado la conjetura de Kepler utilizando métodos geométricos. Sin embargo, Gábor Fejes Tóth (hijo de László Fejes Tóth) afirmó en su reseña del artículo: «En lo que respecta a los detalles, mi opinión es que muchas de las afirmaciones clave no tienen pruebas aceptables». Hales hizo una crítica detallada del trabajo de Hsiang, a la que Hsiang respondió. El consenso actual es que la prueba de Hsiang es incompleta.
Siguiendo el enfoque sugerido por László Fejes Tóth, Thomas Hales, entonces en la Universidad de Michigan, determinó que la densidad máxima de todas las disposiciones podía encontrarse minimizando una función con 150 variables. En 1992, con la ayuda de su estudiante de posgrado Samuel Ferguson, se embarcó en un programa de investigación para aplicar sistemáticamente métodos de programación lineal con el fin de encontrar un límite inferior en el valor de esta función para cada una de las más de 5000 configuraciones diferentes de esferas. Si se pudiera encontrar un límite inferior (para el valor de la función) para cada una de estas configuraciones que fuera mayor que el valor de la función para la disposición cúbica compacta, entonces se demostraría la conjetura de Kepler. Para encontrar los límites inferiores para todos los casos, fue necesario resolver unos 100.000 problemas de programación lineal.
En 2005, Annals of Mathematics publicó un artículo de 100 páginas de Hales en el que describía detalladamente la parte no informática de su demostración. Hales y Ferguson en varios artículos posteriores describieron las partes computacionales, y recibieron el Premio Fulkerson por sus esos artículos en el área de las matemáticas discretas en 2009.
En enero de 2003, Hales anunció el inicio de un proyecto colaborativo para producir una prueba formal completa de la conjetura de Kepler. El objetivo era eliminar cualquier incertidumbre restante sobre la validez de la prueba mediante la creación de una prueba formal que pudiera verificarse con software de comprobación de pruebas automatizado, como HOL Light e Isabelle. Este proyecto se denominó Flyspeck, una ampliación del acrónimo FPK, que significa «Formal Proof of Kepler» (Prueba formal de Kepler). Al inicio de este proyecto, en 2007, Hales estimó que producir una prueba formal completa llevaría alrededor de 20 años de trabajo. Hales publicó un «plan» para la prueba formal en 2012; la finalización del proyecto se anunció el 10 de agosto de 2014. En enero de 2015, Hales y 21 colaboradores publicaron un artículo titulado «A formal proof of the Kepler conjecture» (Una prueba formal de la conjetura de Kepler) en arXiv, en el que afirmaban haber demostrado la conjetura. En 2017, la prueba formal fue aceptada por la revista Forum of Mathematics.
En dimensiones superiores a tres, se conocen los empaquetamientos reticulares más densos de hiperesferas para 8 y 24 dimensiones. Se sabe muy poco sobre los empaquetamientos irregulares de hiperesferas; es posible que en algunas dimensiones el empaquetamiento más denso sea irregular. Esta conjetura se ve respaldada por el hecho de que, en ciertas dimensiones (por ejemplo, 10), el empaquetamiento irregular más denso conocido es más denso que el empaquetamiento regular más denso conocido.
En 2016, Maryna Viazovska anunció una prueba de que el retículo E8 proporciona el empaquetamiento óptimo (independientemente de la regularidad) en el espacio de ocho dimensiones. Poco después, ella y un grupo de colaboradores anunciaron una prueba similar de que la red de Leech es óptima en 24 dimensiones. Este resultado se basó en métodos anteriores que mejoró y que demostraban que estas dos redes están muy cerca de ser óptimas. Antes de que la prueba fuera revisada y publicada formalmente, el matemático Peter Sarnak la calificó de «sorprendentemente sencilla» y escribió: «Basta con empezar a leer el artículo para saber que es correcta». Maryna Sergiivna Viazovska, nacida el 2 de diciembre de 1984, es una matemática ucraniana, actualmente profesora titular y catedrática de Teoría de Números en el Instituto de Matemáticas de la École Polytechnique Fédérale de Lausanne en Suiza. En 2022 fue galardonada con la Medalla Fields por sus resultados.
Una reciente conferencia sobre este tema puede verse en
_____________
Manuel de León (CSIC, Fundador del ICMAT, Real Academia de Ciencias, Real Academia Canaria de Ciencias, Real Academia Galega de Ciencias, Presidente del ICM2006 Madrid y miembro del Comité Ejecutivo de IMU (2007-2024) y del Comité Ejecutivo del ISC (2014-2018).