![]()
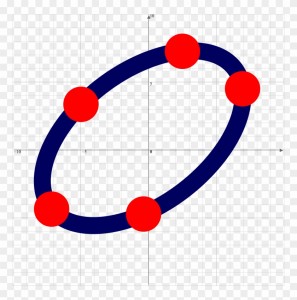
Cinco puntos definen una cónica
Seguimos con nuestro repaso por el mundo de las cónicas y hoy hablaremos de otro de los hitos en su estudio, el Teorema de los cinco puntos, que afirma que cinco puntos de un plano son suficientes para construir una cónica. Afinando más, 3 de esos puntos no pueden ser colineales, porque entonces el resultado sería una cónica degenerada y podría no ser única.
La razón para este resultado es muy simple si consideramos la ecuación general de una cónica:
Ax2 + B xy + Cy2 + D x + Ey + F = 0
entonces, las coordenadas (xi,yi) de los cinco puntos, i = 1, …, 5, deben cumplir la ecuación anterior. Por lo tanto, obtenemos un sistema de cinco ecuaciones con seis incógintas, pero como el sistema es homogéneo, podemos considerar F = 1, y el resultado saldrá de manera inmediata.
La demostración es todavía más evidente cuando se considera la geometría proyectiva, porque en el plano proyectivo RP2 (que se obtiene de R3 identificando todos los puntos de cada recta que pasa por el origen) cada cónica está definida por exactamente cinco números.
Otra cuestión interesante, y que pone de manifiesto esa dualidad entre puntos y rectas, es que se pueden considerar construcciones de cónicas partiendo de m puntos y n rectas, con m+n = 5, donde m y n varían de 0 a 5. En el caso de las rectas, la noción de ser un punto de la cónica se traduce en ser recta tangente a la cónica.
Una de las técnicas modernas más interesantes para estudiar las propiedades de las cónicas consiste en calcular lo que se llama su espacio de moduli. Ya que la ecuación de una cónica incluye 6 coeficientes, A, B, C, D, E, F, y poder eliminar uno, por ejemplo, F, y obtener coordenadas homogéneas (A/F, B/F, C/F, D/F, E/F) (supononiendo, claro está que F no es 0), vemos que existe una correspondencia biyectiva entre cónicas en un plano y puntos del espacio proyectivo RP5 (obtenido de R6 identificando los puntos de las rectas pasando por el origen). Así que RP5 es el espacio de moduli de las cónicas planas. Esto implica que cualquier problema de contar incidencias o tangencias para las cónicas se puede traducir en un problema de intersecciones en el espacio proyectivo RP5 . De hecho, este es el principio en la llamada geometría enumerativa, que tiene en cuenta problemas enumerativos a los que tan aficionados eran los griegos, y es hoy en día una rama muy activa de la geometría algebraica.

Así, podíamos pensar no solo en cuantas cónicas pasan por unos puntos y son tangentes a unas rectas dadas, sino también si son tangentes a unas cónicas prefijadas. Esto enlaza con el famoso problema planteado en 1848 por Jakob Steiner, de la Universidad de Berlín: Dadas cinco cónicas en el plano, ¿cuántas cónicas son tangentes a todas ellas? El propio Steiner dio una respuesta, 7776 = 65, pero estaba equivocado. La respuesta correcta es 3264, como probaron Ernest de Jonquières en 1859, y Chasles en 1864 (aunque el primero no publicó el resultado por respeto a la enorme reputación de Steiner). La geometría enumerativa y la teoría de intersección, dan la respuesta. En el artículo “Enumerative Algebraic Geometry of Conics”, de Andrew Bashelor, Amy Ksir y Will Traves en Amer. Math. Monthly, 115 (8): 701–728, ) se da la respuesta completa a este problema.
Debemos recordar que el llamado Teorema de los cinco puntos tiene una historia antigua. El resultado parece haber sido conocido desde hace mucho, pero no hemos sido capaces de encontrar un autor primero tanto del enunciado como de la prueba. En el artículo “Conic sections through five points classical, projective, conformal”, de Eckhard Matthias Sigurd Hitzer se comenta como en 1844, 200 años después del Teorema de Pascal, el matemático alemán Hermann Grassmann inventósi “Teoría de la extensión”, usó el teorema del francés para encontrar una fórmula explícita de la cónica pasando por cinco puntos.

A medida que se han ido desarrollando las matemáticas, la geometría analítica, la geometría proyectiva, o la moderna geometría algebraica, ha ido proporcionando no solo nuevas demostraciones, sino generalizaciones y nuevos desarrollos matemáticos. Debemos recordar que hay pocos matemáticos relevantes desde los antiguos griegos hasta el sigo XX cuyo nombre no esté asociado de una manera u otra a las cónicas.
Más recientemente, el uso de programas como Geogebra, ha permitido que este y muchos otros resultados puedan ser abordados en el aula de una manera visual, sin que esto suponga ninguna pérdida de rigor matemático. Esto nos lleva a reivindicar la mayor inclusión de contenidos geométricos en los curricula académicos, acompañados de los programas tecnológicos que ayudan a explicarlos y trabajarlos conjuntamente con los alumnos.
—
Agustín Carrillo de Albornoz (Catedrático de Matemáticas y Secretario General de la FESPM y de la FISEM) y Manuel de León (CSIC, Fundador del ICMAT, Real Academia de Ciencias, Real Academia Canaria de Ciencias, Real Academia Galega de Ciencias).

Que recuerdos de cuando estaba en la universidad. Muy buena web.
Buen articulo, me ayudó mucho, gracias!
Muy interesante este artículo. El programa Geogebra no lo conocía.
Interesante, deberían subir más contenido como este.
El mundo de las cónicas… En el cole, que recuerdos!!! De las materias más complejas para mi. Gracias por el contenido.
Es un artículo muy interesante que explica de forma clara y concisa los fundamentos básicos de las matemáticas. Me ha gustado mucho leerlo y me ha ayudado a entender mejor el tema. ¡Gracias por compartirlo!
La publicación es realmente interesante y didáctica. Ha sido un placer leerlo y tomar nota de algunos cálculos, les mandamos cordial saludo.
siempre me ha interesado este tipo de publicaciones matematicas, es la parte del todo!