El Presidente de Estados Unidos que probó el Teorema de Pitágoras

Aprovechando la emisión en Neflix de la miniserie Muerte por una rayo sobre la figura de James Abram Garfield, el vigésimo presidente de los Estados Unidos asesinado por Charles Jules Guiteau, recordamos en esta entrada que fue también un gran aficionado a las matemáticas y publicó una interesante demostración del Teorema de Pitágoras.

En efecto, en 1876, Garfield desarrolló una demostración trapezoidal del teorema de Pitágoras, publicada en el New England Journal of Education. El historiador de las matemáticas William Dunham escribió que el trabajo trapezoidal de Garfield era «realmente una demostración muy ingeniosa». Según el Journal, Garfield llegó a la demostración «en diversiones matemáticas y discusiones con otros miembros del Congreso». La demostración apareció impresa en el New-England Journal of Education (Vol. 3, n.º 14, 1 de abril de 1876).

James A. Garfield (19 de noviembre de 1831 – 19 de septiembre de 1881), fue el vigésimo presidente de los Estados Unidos. En el momento de la publicación de la demostración, Garfield era congresista por Ohio. Garfield tuvo unos orígenes muy humildes, y a base de esfuerzo, logró estudiar Derecho y convertirse en abogado. Fue elegido senador por Ohio y cuando se inicia la guerra de Secesión, desempeña un papel muy destacado en el ejército de la Unión. Al terminar la guerra civil es elegido congresista (siempre militó en el partido republicano) y en la convención de Chicago, es elegido candidato a la presidencia, elecciones que gana. Asumió así el cargo de presidente el 4 de marzo de 1881 y ocupó el cargo hasta su muerte el 19 de septiembre de 1881, tras sucumbir a las heridas sufridas cuando fue tiroteado en un atentado en julio. Como presidente, luchó contra la corrupción de Washington, basada en la concesión de prebendas a cambio de apoyos parlamentarios. Fue precisamente esta lucha lo que llevó a Charles Jules Guiteau, un abogado desequilibrado y buscador de cargos a disparar contra Garfield, quien no le había concedido un puesto consular que había solicitado.

Garfield es, hasta ahora, el único presidente de los Estados Unidos que ha contribuido con algo original a las matemáticas. No parece que el actual ocupante de la Casa Blanca, aunque también republicano, vaya por el mismo camino de la apreciación de la ciencia (señalemos ademas que fue un defensor de la bajada de aranceles, que habían subido mucho debido a la guerra civil).

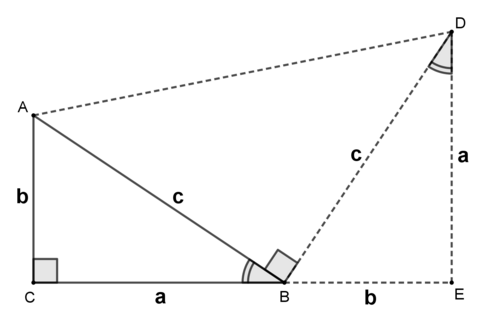
Recordemos su demostración con ayuda de la figura. En ella, ABC es un triángulo rectángulo con el ángulo recto en C. Las longitudes de los lados del triángulo son a, b y c. El teorema de Pitágoras afirma que 

c²=a²+b².

Para demostrar el teorema, Garfield trazó una línea a través de B perpendicular a AB y en esta línea eligió un punto D tal que BD=BA. A continuación, desde D trazó una perpendicular DE sobre la línea extendida CB. A partir de la figura, se puede ver fácilmente que los triángulos ABC y BDE son congruentes (basta calcular los tres ángulos de ambos). Dado que AC y DE son perpendiculares a CE, son paralelos, por lo que el cuadrilátero ACED es un trapecio. El teorema se demuestra calculando el área de este trapecio de dos maneras diferentes. La primera usando la fórmula del área de un trapecio (semisuma de las bases por la altura), y la segunda sumando las áreas de todos los triángulos. De ahí se sigue fácilmente el teorema de Pitágoras.

_____________

Manuel de León (CSIC, Fundador del ICMAT, Real Academia de Ciencias, Real Academia Canaria de Ciencias, Real Academia Galega de Ciencias, Presidente del ICM2006 Madrid y miembro del Comité Ejecutivo de IMU (2007-2024) y del Comité Ejecutivo del ISC (2014-2018).