J.M. Sanz-Serna en Matemáticas en la Residencia

La segunda conferencia del Ciclo “Matemáticas en la Residencia” promete ser de gran interés.  El conferenciante es, sin duda, uno de los mejores matemáticos españoles y un magnífico divulgador. Estamos hablando de J.M. Sanz-Serna, catedrático de la Universidad de Valladolid y Académico de la Real Academia de Ciencias. Ha recibido innumerables premios y reconocimientos a lo largo de su dilatada trayectoria, entre otros, el premio Dahlquist de la Society for Industrial and Applied Mathematics y el premio Iberdrola de Ciencia y Tecnología.

Otro aspecto que merece destacarse,  es que Sanz-Serna fue conferenciante invitado en el Congreso Internacional de Matemáticos de Zurich en 1995, un honor del que muy pocos matemáticos del mundo pueden presumir.

El día 8 de abril a las 19:30, en la Residencia de Estudiantes, J.M. Sanz-Serna nos deleitará con la conferencia

De la piedra al ordenador pasando por la matemática

El tema es bien conocido por el profesor Sanz-Serna, pues su línea de investigación se centra en la Matemática Aplicada y, en concreto, en el campo de la integración numérica de ecuaciones diferenciales,  es decir, en el diseño de métodos que, usando el ordenador, nos permiten resolverlas aproximadamente. Las ecuaciones diferenciales nos ayudan a modelar y entender muchos  procesos naturales y tecnológicos, por lo que constituye un campo de investigación de considerable importancia.  De hecho, Sanz-Serna es reconocido como la gran figura internacional de la Integración Geométrica (término acuñado por él mismo). En dicho campo, se introducen métodos numéricos que, además de aproximar adecuadamente a las ecuaciones diferenciales que se pretende analizar,  comparten con éstas la propiedad de preservar  estructuras geométricas  (constantes del movimiento, formas simplécticas, de Poisson…). Estos métodos han demostrado una extraordinaria eficacia en las simulaciones numéricas tanto en el nivel cuantitativo como cualitativo. Así,  es frecuente utilizar estos métodos numéricos geométricos en simulaciones a tiempos muy largos, millones de años, del sistema solar.

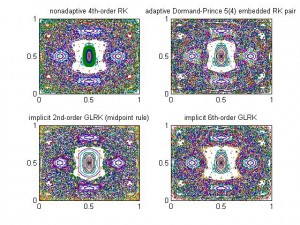
No asustemos más al lector de nuestro blog con tecnicismos, pues la conferencia que impartirá Sanz-Serna, será accesible para todos los públicos. Sólo hará falta una cosa para asistir…  tener  un apasionado interés por la cultura, de la que la ciencia forma una indisoluble parte.

Además, el 8 de abril,  para presentar a nuestro conferenciante, también contaremos con la presencia de un grande la ciencia española, el profesor Amable Liñán, Catedrático de la Universidad Politécnica de Madrid y  Premio Príncipe de Asturias de Investigación Científica y Técnica.

La conferencia se impartirá en español, pero también habrá traducción simultánea al inglés.

Os esperamos a todos el día 8 de abril, en una charla que seguro nos hará disfrutar de una extraordinaria velada.

__________________________________________

David Martín de Diego, Investigador Científico del Instituto de Ciencias Matemáticas (ICMAT)