![]()
La misteriosa ley de Zipf
De este blog y de sus diez años dedicados a las matemáticas, queda claro que las mismas tienen muchas aplicaciones en otros campos: en la biología, medicina, en las finanzas, ymuy especialmente, en la física.
En la biología, por ejemplo, las matemáticas han desarrollado modelos del equilibrio y supervivencia de las especies. Son los llamados modelos de Lotka-Volterra, en los que se predice la coexistencia de dos poblaciones: la de presas y depredadores, o la invasión parasitaria sobre otro organismo. El modelo consiste en dos ecuaciones diferenciales acopladas, regidas por ciertas condiciones iniciales y parámetros que dan cuenta de las condiciones ecológicas del entorno.
En la medicina, las aplicaciones son muy numerosas: desde el cálculo de las dosis de fármaco pertinentes a la explicación de un diagnóstico radiológico. Especialmente, se están desarrollado grandes modelos matemáticos (teoría de grafos, por ejemplo) para la explicación de los procesos neuronales.
En finanzas, existen modelos predictivos del mercado (aún muy poco refinados, de lo contrario la inversión en valores estaría más concurrida que la de los abuelos dirigidos por brokers del mismo banco al que han confiado todos los ahorros de su vida laboral, como hemos visto en la última crisis económica). Por ejemplo, los modelos de Black-Scholes tientan la subida de precio de un activo. Sin embargo, sus redefiniciones son continuas, y su rango de aplicación va a opciones europeas o inversiones con dividendos.
En física, es imposible elegir un ejemplo característico de aplicación entre los centenares de modelos teóricos basados en las matemáticas más formales (invitamos a seguir los que aparecen en el arxiv diariamente). Las aplicaciones a la física pueden dividirse en ramas de las matemáticas con su relación a su rama física correspondiente. Por ejemplo, la geometría diferencial es el punto de partida de la relatividad general, pero también en la termodinámica. El análisis matemático tiene un gran peso en la teoría de fluidos y el álgebra lineal y el análisis funcional son primordiales en mecánica cuántica y sus operadores matriciales.
Sin embargo, las matemáticas parecen no haber llegado a calar tan intensamente en otros campos no científicos, como la biblioteconomía o la lingüística. Para desmentir su carencia de aplicación en el campo de las letras, hoy queremos describir la llamada ley de Zipf.
En los años cuarenta, el lingüista George Zipf se dio cuenta de que las palabras y su número de apariciones en textos, seguían alguna ley especial. La palabra más utilizada ocuparía el número uno en el ranking, el número dos se corresponde con la segunda palabra más veces repetida, etc. Así, se guardaba una estrecha relación entre el número de apariciones de las palabras más populares. La primera palabra más utilizada aparecía el doble de veces que la segunda y tres veces más que la tercera, y sigue el patrón según esta norma. Por ejemplo, en el Mago de Oz, de Franz L. Baum, publicado en 1908, la palabra más frecuente fue “the” con 3137 apariciones, la segunda es “and” con 1544 apariciones, y la tercera “to” aparece 1107 veces. La ley dice que
Pn ≈ 1⁄na
donde P n es la frecuencia de una palabra en el orden n y el exponente a es aproximadamente 1.
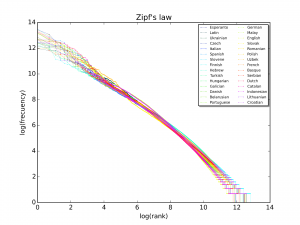
George Kingsley Zipf (1902–1950) fue un lingüista americano, nacido en Freeport, Illinois, que se encontró con este fenómeno en sus estudios estadísticos de filología comparada. Estudió en Harvard, Bonn y Berlin, siendo luego profesor en Harvard. Digamos como curiosidad de que fue Zipf quien popularizó esta ley, la misma parece haber sido descubierta previamente por el estenografo francés Jean-Baptiste Estoup y también por el físico alemán Felix Auerbach en 1913.

Esta ley se convirtió en una ley curiosa que no sólo describe el comportamiento de la redacción y el uso de las palabras, sino que también distribuía, por ejemplo, el salario de los hombres más adinerados del planeta; en efecto, en un mismo país, la persona con mayor sueldo recibía el doble que el siguiente en orden descendente.
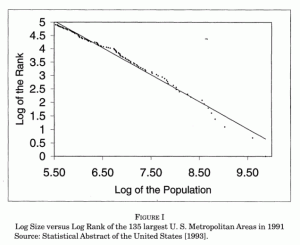
Otro uso de esta ley fue para el cálculo de habitantes en las ciudades más pobladas de un mismo país. También se corroboró que, aproximadamente, el número de personas en la capital más poblada es el doble que en la segunda capital más poblada y el triple que en la tercera, etc. Por ejemplo, los números concuerdan con las capitales estadounidenses: según el censo del 2010, Nueva York tenía una población total de 8.175.133 personas, siendo la siguiente capital más poblada Los Ángeles, con 3,792,621 habitantes y las siguientes capitales en el ranking, respectivamente, Chicago, Houston and Filadelfia con 2,695,598, 2,100,263 y 1,526,006 . Efectivamente, parece que la ley se cumple. En este citadísimo artículo de 1999 el economista Xavier Gabaix describió esta ley para las ciudades como una ley de potencias, y el gráfico sería algo así:
La ley parece cumplirse hasta en el caso de ciudades con crecimiento caótico. Sin embargo, parece que los números no se siguen para ciudades de pequeño tamaño. Se bajara que la ley de Zipf sea un reflejo del crecimiento de ciudades con condiciones económicas similares, como pueden ser las integradas en la Unión Europea.
Otra de las leyes matemáticas aplicadas a la sociología y las poblaciones es la regla de los tres cuartos. Esta regla es aplicable al cálculo de la cantidad de recursos necesarios dependiendo del crecimiento de la ciudad. A primera vista, diríamos que si el número de habitantes de una ciudad es el doble que el otra, el número de gasolineras necesarias sería el doble. Sin embargo, el número de recursos se corresponde con los mencionados ¾, y la eficiencia de la ciudad será la misma con sólo un 77% más de gasolineras.
Existen variaciones de la ley de Zipf e investigaciones recientes concernientes a tal ley. Los investigadores Álvaro Corral, Isabel Moreno García y Francesc Font Clos, del Centro de Recerca Matemática (CRM) de Barcelona, vinculado a la Universidad Autónoma de Barcelona, han completado un análisis a gran escala de miles de textos digitalizados para el primer tratamiento empírico de la ley de Zipf. Su trabajo se basaba en el estudio de más de 30.000 volúmenes en inglés para la formulación clara de la ley desde el punto de vista probabilístico: una que no asocie probabilidad a las palabras, sino variables numéricas.
Se obtuvo una ley equivalente de contar el número de apariciones de una palabra, y una segunda estadística que de cuenta del número de palabras diferentes que aparecen un número dado de veces. Así, el número de palabras que aparecen una única vez es el cuádruplo del número de palabras que aparecen dos veces, el nónuplo del número que aparecen tres veces, y sucesivamente. Las dos leyes de las frecuencias se han considerado hasta ahora quasiequivalentes, salvo porque la frecuencia de las palabras no es una variable continua.
La falta de empiricidad había derrotado muchas de estas teorías. Sin embargo, los nuevos métodos computacionales pueden simplificarnos mucho su corroboración. Como hemos visto, el estudio relatado anteriormente es muy reciente, del 2015, y se ha llevado a cabo gracias al software accesible del siglo XXI.
Sin embargo, todavía no está muy clara la explicación de la ley de Zipf, una ley empírica. Aparte de las explicaciones estadísticas, se habla por ejemplo de una ley del mínimo esfuerzo por parte de los que hablan, escriben o escuchan que para simplificar sus frases elijen las palabras mas corrientes, o el principio de que el éxito atrae el éxito. El tema es intrigante y requerirá mas y mas interés en el futuro inmediato.

Gracias a a revolución informática y su crecimiento exponencial, con la creación diaria de nuevas apps, estamos viviendo la era del Big Data. Esta ciencia se dedica a la clasificación y almacenamiento de volúmenes de datos que no pueden ser tratados normalmente, debido su ingente cantidad. Para ello, se están desarrollando nuevas herramientas en software y nuevas modas estadísticas. El concepto engloba infraestructuras, tecnologías y servicios creados para el procesamiento de estos conjuntos de datos estructurados, no estructurados o semi-estructurados (mensajes en redes sociales, señales de móvil, archivos de audio, sensores, imágenes digitales, datos de formularios, emails, datos de encuestas, logs etc,) que pueden provenir de sensores, micrófonos, cámaras, escáneres médicos, etc.
En el ICMAT se ha puesto en marcha el Laboratorio Robert Grossman, en el que este experto mundial que trabaja en la Universidad de Chicago colaborará con investigadores del instituto en estos temas. A la vez, la recientemente lanzada Fundación CorBI (Coruña Biomedical Institute) tiene entre sus objetivos el desarrollo de proyectos relacionados con Big Data y está cerrando importantes colaboraciones en los Estados Unidos.
Les dejamos con este video que explica con detalle la ley de Zipf:
[youtube]https://www.youtube.com/watch?v=fCn8zs912OE[/youtube]
—
Manuel de León (CSIC, Fundador del ICMAT, Real Academia de Ciencias, Real Academia Canaria de Ciencias, ICSU) y Cristina Sardón (ICMAT-CSIC).


[…] superior a 1. Revisitamos en esta entrada este tema, que ya fue objeto de varias más en el pasado: La misteriosa ley de Zipf y La ley de Zipf para la seña, esta última en la que analizamos si la ley se cumplía para el […]