![]()
La conjetura del girasol
Los matemáticos han mostrado siempre una gran prelidección por los girasoles, no olvidemos la relación entre las espirales a izquierda y derecha de sus semillas, siguiendo siempre el patrón marcado por la sucesión de Fibonacci. No es pues de extrañar que Paul Erdős y Richard Rado conjeturaran en 1960 un excitante problema sobre estas plantas, que acaba de tener un avance muy importante.

El problema que plantearon Erdös y Rado preguntaba con que frecuencia uno esperaría entontrar patrones que se asemejaran a los girasoles el analizar una colección muy grande de objetos. Intentaremos en los párrafos que siguen dar una explicación más detallada del problema.


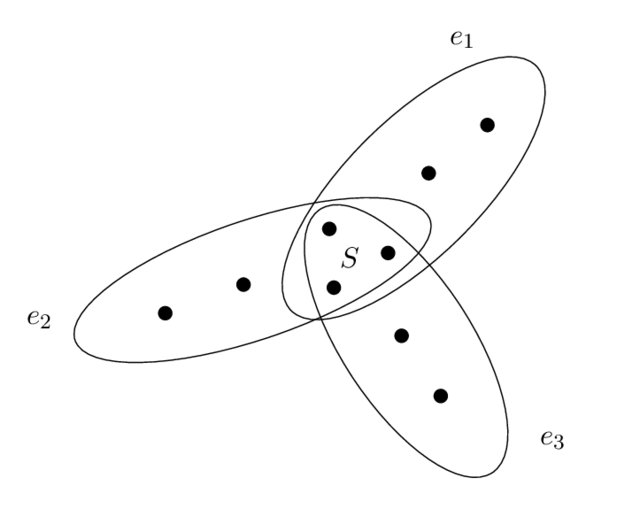
Primero tendremos que definir lo que los matemáticos entendemos por un giraols: “un girasol de r pétalos es una colección de r conjuntos tales que la intersección de cada par es igual a la intersección de todos”. Lo que Erdös y Rado probaron en su día es lo que se llama el Lema del girasol: para un r fijado, r mayor o igual que 3, cualquier familia de conjuntos de w elementos con al menos ww conjuntos, debe contener un girasol. Si los conjuntos son S1, …, Sr, entonces la intersección de todos ellos
K = S1 ∩ … ∩ Sr
se llama el núcleo y los complementarios S1\K, …, Sr\K son los pétalos.
El resultado se ve en toda su dimensión si pensamos que para 100 puntos necesitaríamos 100100 conjuntos, una cantidad enorme. Así que Erdös y Rado, tras probar su lema, conjeturaron que debía haber una cota mucho más baja, que debería existir una constante c(r) tal que si el número de conjuntos de la familia dada era mayor o igual que c(r)w, entonces esa familia debería contener un girasol. Ellos pensaban que el problema era muy sencillo, pero no consiguieron probarlo, y no ha habido resultados significativos hasta este último de este año, 60 años después de formularse la conjetura.
La prueba de este resultado es interesante porque combina matemáticas fundamentales con la teoría de la computación. Los autores (Ryan Alweiss, Shachar Lovett, Kewen Wu y Jiapeng Zhang) del artículo en cuestión, titulado “Improved bounds for the sunflower lemma”, combinaron sus experiencias en ambos campos, y mediante el uso de las llamadas funciones booleanas, consiguieron encontrar una cota satisfactoria; basta con (log w)w para garantizar un girasol.
Recordemos que una función booleana lleva palabras (codificadas con ceros y unos) en un 0 o en un 1; es decir, funciones f: Bn → B, donde B = {0, 1}.
Si alguien se pregunta qué interés puede tener un problema como este para el resto de la humanidad que no se dedica a las matemáticas, decirle que este es doble. Por una parte, es una muestra de cómo cuando aumentamos los datos, aparecen como venidos de la nada patrones; y por otra, es un mestizaje entre matemáticas y computación, que muestra como esta última descansa precisamente en los fundamentos de las matemáticas más abstractas.
En este video, podemos asistir a una conferencia sobre el tema impartida por uno de los autores del citado artículo Jiapeng Zhang, de la Universidad de Harvard:
[youtube]https://youtu.be/DvIO_Po6kfs[/youtube]
Diremos finalmente que este problema es el objeto del proyecto Polymath número 10: Improving the bounds for the Erdos-Rado sunflower lemma, puesto en marcha el 2 de noviembre de 2015.
___
Manuel de León (CSIC, Fundador del ICMAT, Real Academia de Ciencias, Real Academia Canaria de Ciencias).

«Lo que Erdös y Rado provaron en su día…».
ProVaron? Aarrggg!
La b y la v están demasiado cerca en el teclado, gracias por avisar.
Muy interesante. Las matemáticas son el lenguaje del Universo.
The information shared is very good, thanks to the author, it helps me a lot, I am looking for it.
esperaría entontrar patrones