![]()
¿Por qué el número π resulta tan fascinante?
ππHoy es 14 de marzo de 2020, 3,14 si usamos la manera anglosajona de contar los días del año, la aproximación decimal más popular del número π, y por eso los matemáticos de todo el mundo nos pusimos de acuerdo para solicitar que en ese día se conmemorara el Día Internacional de las Matemáticas, día proclamado por la UNESCO. Digamos que es un día merecido y no solo por el interés de π.
En esta página web se pueden econtrar los más de 1000 eventos que se han organizado en unos 100 países del mundo, atendiendo a la llamada de la Unión Matemática Internacional (IMU en sus siglas inglesas). Algunos de estos eventos tendrán las dificultades derivadas de la pandemia ocasionada por el coronavirus, pero ni eso será capaz de enfriar el entusiasmo de los matemáticos. Cada año se elegirá un tema que para 2020 es “Matemáticas en todos los sitios”.

La pregunta que nos podemos hacer es: ¿por qué π? ¿Qué tiene de especial este número que tanto fascina a matemáticos y no matemáticos? La primera vez que nos encontramos a π en nuestras vidas es en la escuela cuando aprendemos a calcular la longitud de una circunferencia, 2πr, donde r es el radio. Con más formalidad matemática diríamos que π es la relación entre la longitud de la circunferencia y el diámetro (como sentenció Euclides). Es una de las maravillas de las matemáticas, nos sirven para probar esta afirmación, que es la que ha dado el símbolo a π, por la palabra griega perímetro. El primero en usar esta notación fue el inglés William Oughtred, aunque fue el matemático galés William Jones el que la propuso en 1706. Como casi siempre, Leonhard Euler la popularizó en su obra Introducción al cálculo infinitesimal, de 1748.


Y una vez constatado esta verdad geométrica, debemos conocer su valor numérico. Esto ha sido un empeño desde la más remora antigüedad. Ya en la Biblia se la da el valor aproximado de 3. En el Libro de los Reyes, se describe como Salomón hizo construir su palacio, y se puede leer:
“Hizo fundir asimismo un mar de bronce de diez codos de un lado al otro, perfectamente redondo; su altura era de cinco codos, y lo ceñía alrededor un cordón de treinta codos”.
Digamos que un mar (de bronce) era una pila de agua para las abluciones.

Los antiguos egipcios le dieron el valor aproximado de 3,16 (en el papiro de Rhind), y en la antigua Mesopotamia se le daba el valor de 3 o 3,125 en otros casos. Pero fue el genio de Arquímedes (siglo II a.C.) el que comenzó a aproximar de una manera sistemática el valor de π, construyendo polígonos inscritos y circunscritos a un círculo dado. 500 años más tarde, Ptolomeo ya lo calculaba con más precisión: 3,1416. Los chinos y los indios también hicieron aproximaciones parecidas.
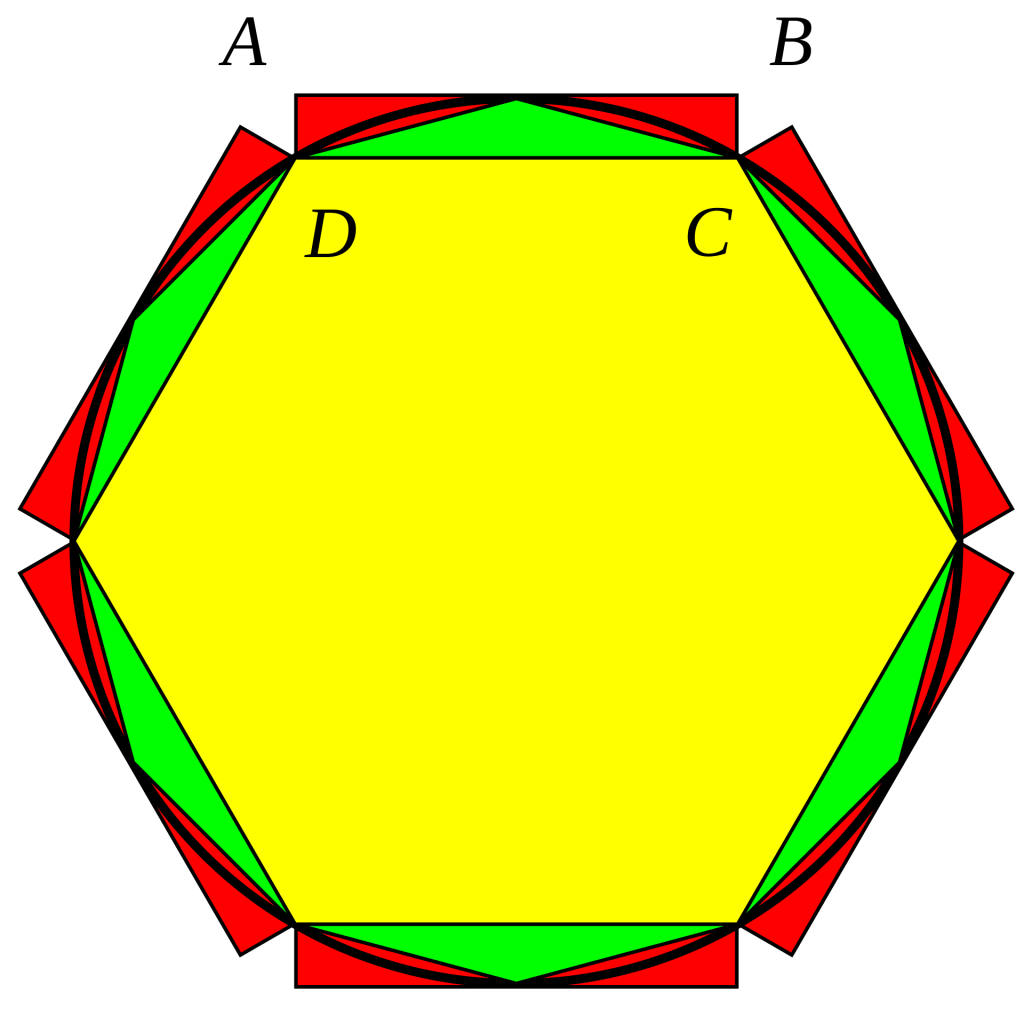
De estas aproximaciones, puramente geométricas como la de Arquímedes, se pasó a las analíticas, en cuanto el cálculo diferencial se fue desarrollando (existen formas maravillosas de escribir el número π como suma de series). Y ahí comenzó una carrera que dura hasta nuestros días para calcular más y más números de la expresión decimal de π, especialmente cuando los ordenadores aumentaron de manera extraordinaria nuestra potencia de cálculo.
Todo este esfuerzo sabiendo que es inútil, nunca conoceremos la expresión decimal completa de este maravilloso número. Sabemos, como demostró Johann Heinrich Lambert en 1761, que es un número irracional, es decir, no se puede expresar como una fracción, y por lo tanto su expresión decimal no termina nunca. También sabemos que es un número trascendente, es decir, que no es la raíz de ningún polinomio de coeficientes enteros, tal y como demostró en 1882, Carl Louis Ferdinand von Lindemann. Sin embargo, seguiremos calculando más y más números decimales de π, buscando el milagro irracional en uno de los números más irracionales.
__
Manuel de León (CSIC, Fundador del ICMAT, Real Academia de Ciencias, Real Academia Canaria de Ciencias, Real Academia Galega de Ciencias).

