Cómo se resuelve un sistema de ecuaciones: historia reciente y estado del arte

El Premio de Investigación José Luis Rubio de Francia, que otorga anualmente la Real Sociedad Matemática Española, ha sido concedido en 2010 a Carlos Beltrán Álvarez, de la Universidad de Cantabria, por, entre otros resultados, la resolución junto a Luis Miguel Pardo del problema 17 del famoso listado propuesto por Steve Smale al finalizar el pasado siglo, y cuyo enunciado es: ¿Puede encontrarse un cero de n ecuaciones polinomiales complejas, por medio de un algoritmo uniforme en tiempo polinomial en promedio? En esta entrada del blog, Carlos Beltrán y Luis Miguel Pardo nos ofrecen un resumen de su trabajo.

Cómo se resuelve un sistema de ecuaciones: historia reciente y estado del arte

 Carlos Beltrán y Luis Miguel Pardo. Depto. MATESCO, Univ. Cantabria

Supongamos que nos dan n ecuaciones con n incógnitas, y que nos piden encontrar un cero del sistema, esto es un vector de n coordenadas (reales o complejas) en el que todas las ecuaciones se anulan simultáneamente. ¿Cómo debemos proceder? Algunas reflexiones iniciales son:

1. El caso de ecuaciones lineales (las incógnitas no se elevan a potencias superiores a 1) se resuelve desde tiempo inmemorial y ha quedado en las mentes jóvenes asociado al nombre de Gauss.
2. Desde las civilizaciones egipcia y babilónica, diversos procedimientos se desarrollan para tratar el caso de una ecuación con una incógnita y grado 2, que se resuelve mediante una fórmula que involucra una raíz cuadrada. Aceptar la presencia de raíces (radicales) o buscar métodos para calcular aproximaciones al valor numérico de esa raíz conducirá a la futura subdivisión entre métodos numéricos y simbólicos para el tratamiento y resolución de ecuaciones.
3. Se denominó “resolución por radicales” al intento de expresar mediante raíces (cuadradas, cúbicas, etc…) las soluciones de une ecuación dada. En el renacimiento italiano existían, incluso, concursos públicos, con suculentos premios, para resolver este tipo de ecuaciones. Los “campeones” de la época sería gente como Scipione del Ferro, Lodovico Ferrari, Niccolo Fontana (alias “Tartaglia”) o Gerolamo Cardano. En su tratado “In artem analyticam isagoge”, François Viète exhibe varias fórmulas (esencialmente tomadas de Cardano) para expresar con radicales soluciones de ecuaciones polinomiales de grados 3 y 4. Estas fórmulas perviven como las fórmulas de Cardano-Viète .
4. Para grado 5 no hay ni puede haber una fórmula que, incluso admitiendo radicales, exprese las soluciones  como funciones de los coeficientes. Esta fue una de las conclusiones de los trabajos de dos brillantísimos matemáticos, muertos en plena juventud: Niels Hendrik Abel y Evariste Galois. Ninguno de los dos superó los 27 años.
5. En el caso de una ecuación con una incógnita, el medalla Fields Steve Smale inició a principios de los años 80 un importante esfuerzo para fundamentar los algoritmos numéricos (algoritmos que aproximan las soluciones) a través de un estudio profundo del operador de Newton, su convergencia y las cantidades que lo controlan. Adicionalmente, adaptó una de las pruebas de Gauss del Teorema Fundamental del Álgebra, basada en deformar la ecuación a resolver a otra ecuación más fácil de resolver. Esto conduce a los métodos llamados de deformación homotópica o de continuación de caminos, que se detallarán más abajo.
6. El caso general (resolver un sistema de n ecuaciones polinomiales y n incógnitas) es uno de los problemas centrales de la Geometría Algebraica. No sólo no hay fórmulas para las soluciones sino que la geometría del conjunto de soluciones juega un papel relevante, haciendo necesaria la interacción entre Geometría, Algorítmica y Métodos Numéricos.
7. No parece probable que haya una forma fácil de enfocar el problema general (especialmente cuando el número de ecuaciones sea superior al número de variables involucradas). en ese caso nos enfrentamos a uno de los Problemas del Milenio, propuestos por el Instituto Clay: la Conjetura de Cook. Esto se debe a que cualquier problema NP-completo (pongamos, el problema de la mochila) se puede escribir fácilmente como un sistema de n+1 ecuaciones y n incógnitas complejas. En el caso de buscar solamente soluciones reales, basta con una ecuación en n incógnitas. Por lo tanto, si existiese un algoritmo rápido para encontrar soluciones de sistemas de ecuaciones polinomiales, tendríamos que P=NP, lo que supondría un cambio enorme en nuestra concepción de la Informática y de las Matemáticas.
8. Si tratamos de describir todas las soluciones de un sistema de ecuaciones podemos tener problemas: el número de ellas puede ser infinito si aparecen funciones trascendentes, y si son polinomios en general el número de soluciones es el producto de los grados (conocido como el número de Bézout). Esto es, si tenemos n ecuaciones de grado 2 en n variables, tendremos genéricamente 2ⁿ soluciones, lo que para n mayor que, pongamos, 50,  hace imposible siquiera escribir una aproximación de cada una de ellas, ¡no digamos calcularlas!

Pero no todo está perdido: por ejemplo, aunque el número de incógnitas y de ecuaciones sea mayor de uno, todavía podemos aplicar el método de Newton. Éste consiste en tomar un candidato inicial a solución, llamémoslo x, y realizar la iteración que lleva x a x-Df(x)^-1f(x), donde Df(x) es la matriz diferencial de f en x. No siempre esta matriz es invertible, pero ciertamente lo que podemos hacer es intentar calcular esta cantidad, y confiar en que después de unas cuantas iteraciones nos encontraremos cerca de una solución del sistema. ¿A qué se debe este optimismo? Pues por ejemplo a que si x es un cero exacto del sistema, entonces la iteración de Newton lo deja como está – o sea que los ceros del sistema son puntos fijos del operador de Newton, lo que hace razonable seguir este proceso.

En la práctica, muchas veces elegimos un x, iteramos Newton unas pocas veces, y no nos parece que la sucesión generada converja a ningún lugar. Así que el optimismo del que hablábamos es en efecto un excesivo optimismo. Sin embargo, Gauss (y más recientemente, entre otros, Steve Smale) proponen una cierta forma de escapar de este problema, utilizando los llamados métodos de homotopía.

1. Llamemos f₍₁₎ al sistema que queremos resolver. Consideremos  otro sistema f₍₀₎ que sea sencillo, en el sentido de que tenga una  solución conocida. Ahora debemos unir g con f con  algún camino, pongamos el segmento f_(t)=(1-t)f₍₀₎+tf₍₁₎, donde t es un número entre 0 y 1. En general, si pensamos que f₍₀₎ y f₍₁₎ son sistemas polinomiales donde los polinomios de f₍₀₎ y de f₍₁₎ tienen el mismo grado, podemos pensar que el segmento f_(t) está contenido en el espacio vectorial que forman los sistemas polinomiales de grado acotado. Si nuestros sistemas no son polinomiales, tendremos que buscar alguna alternativa que nos parezca razonable.
2. Ahora consideremos el conjunto V={(f,x):x es un cero de f}, que es una subvariedad diferencial y a la vez algebraica  del espacio producto {sistemas}x{vectores}, llamado comúnmente la variedad solución. Dado que la curva f_(t) está contenida en el espacio de sistemas, bajo ciertas condiciones de genericidad, podemos suponer que existe un “levantamiento”, esto es que el camino f_(t) puede ser levantado a un camino (f_(t),x_(t)) contenido en V. Por tanto, se tiene que f_(t)(x_(t))=0. Derivando esta expresión con respecto al tiempo se obtiene una ecuación diferencial ordinaria para x_(t). Como además tenemos las condiciones iniciales dadas por x₍₀₎, podemos seguir la curva x_(t) utilizando métodos estándar de ecuaciones diferenciales para aproximar la solución x₍₁₎ de f₍₁₎. En la práctica, se combinan un método tipo Runge-Kutta o Euler con el método de Newton para mantenernos cerca del camino. Esta técnica de pasar al espacio producto se remonta a la desingularización de Room-Kempf, utilizada desde los años 40 del pasado siglo por los Geómetras Algebraicos.

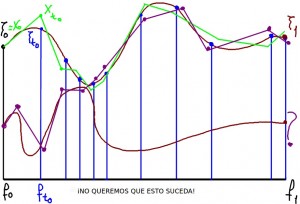
Claro, para que todo esto funcione hay que precisar muchas cosas: el método que se usa para resolver la ecuación diferencial, la existencia de un levantamiento, y el par inicial  (f₍₀₎,x₍₀₎). Con la experiencia de muchos años, los matemáticos han ido programando métodos que realizan esta labor y que funcionan muchas veces. ¡Sin embargo, no es fácil garantizar que de hecho vayan a funcionar, ni que vayan a dar la respuesta buscada! El estudio matemático de algoritmos busca clarificar los puntos oscuros que aparecen siempre que un método se utiliza sin que su buen funcionamiento esté claramente justificado y garantizado por un teorema. En este contexto, se busca evitar un escenario de cruce de soluciones como el que aparece en la figura 1.

Durante la década de los 80, muchos autores se dedicaron a analizar este método de resolución, tratando de explotar un uso inteligente del operador de Newton. Podemos citar a E. L. Allgower, K. Georg, A. Morgan, C. B. Garcia, W. I. Zangwill y J. Renegar entre muchos otros. Sin embargo, la aportación esencial vino de la mano de la colaboración entre Michael Shub y Stephen Smale. Su principal aportación es que encuentran y analizan al detalle una cantidad (el número de condicionamiento no lineal), con fuerte significado métrico y geométrico, que controla permite controlar ese proceso de “aproximar la curva (f_(t),x_(t))”, y además (a un nivel más técnico) contiene información sobre las propiedades intrínsecas de las soluciones aproximadas. 

El caso univariado se resuelve a satisfacción (con un algoritmo tratable) ya a mediados de los años 80, fruto de esta colaboración entre M. Shub y S. Smale. A finales de los 80 quedaba el gran salto cualitativo del paso al caso multivariado: n ecuaciones polinomiales en n incógintas.

M. Shub y S. Smale ponen manos a la obra en una excelente serie de trabajos (popularmente conocidos como Bézout I a Bézout V) en la que fundamentan lo esencial del comportamiento y complejidad de los algoritmos para la resolución de sistemas de ecuaciones polinomiales por métodos numéricos, basados en deformaciones homtópicas. Sin embargo, no consiguen culminar su programa, abandonando en 1993 el objetivo de generalizar al caso multivariado lo ya obtenido por ellos mismos en el caso univariado a mediados de los 80. Surge así, por ejemplo, la Conjetura de Shub y Smale aún irresuelta.

A finales del pasado siglo Smale elabora su famosa lista de 18 problemas (a imitación de la famosa lista de Hilbert) entre los que se incluyen problemas como la Conjetura de Cook o la Conjetura de Poincaré y, entre ellos, enuncia el problema decimoséptimo:

PROBLEM 17:

“Can a zero of n complex polynomial equations in n unknowns be found approximately, on the average, in polynomial time with a uniform algorithm?

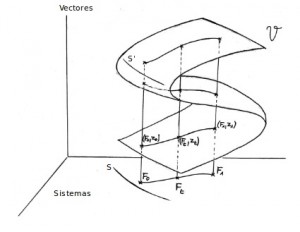
El punto más delicado es la elección de (f₍₀₎,x₍₀₎): ¿cómo podemos elegirlos para garantizar que siempre –o casi siempre- existirá el levantamiento y será fácil de seguir? La existencia del levantamiento puede verse gráficamente en la figura 2: el conjunto de puntos S’ (los pares donde la matriz diferencial no tiene rango máximo) es lo que nos puede causar problemas, por lo que si queremos garantizar que no tendremos problemas los sistemas deben moverse fuera de S (la proyección de S’).

Hacemos ahora un pequeño resumen histórico de los resultados de las dos últimas décadas en esta dirección:

1. En su trabajo de 1993, Shub y Smale demostraron que, fijado n y una lista de grados de los polinomios, existe un par inicial (f(0),x(0)) que garantiza que casi siempre el método  de homotopía descrito arriba funcionará correctamente. Desgraciadamente su prueba es puramente existencial y su resultado no implica la existencia de un algoritmo propiamente dicho. En su Conjetura final (1993), sugieren un par inicial que podría satisfacer esas propiedades milagrosas. Esta Conjetura sigue abierta.
2. El problema quedó abandonado durante 15 años. En el año 2006 Beltrán y Pardo anuncian que disponen de un algoritmo probabilista, uniforme que resuelve en tiempo polinomial la mayoría (en términos probabilísticos, con gran probabilidad) de los sistemas de n ecuaciones polinomiales con n incógnitas. El resultado final se publicará en 2008.  La novedad consiste en abandonar, momentáneamente, la búsqueda de un par inicial milagroso y sustituirlo por un método de diseño de un conjunto de pares iniciales (llamado cuestor) y probar que una elección aleatoria de pares en ese conjunto produce un buen par inicial con alta probabilidad.
3. Posteriormente, publicado en 2009, estos mismos autores combinan el método de deformación homotópica del último trabajo de Shub y Smale (Bézout V) con el método de selección aleatoria de pares y consiguen demostrar la primera respuesta positiva al Problema 17 de Smale: existe un algoritmo uniforme que resuelve n ecuaciones polinomiales en n incógnitas en tiempo promedio polinomial.
4. Este resultado produjo un fuerte impacto en la comunidad de especialistas en complejidad de algoritmos numéricos, renaciendo el interés por este problema. Así, M. Shub rediseña el método de deformación homotópica, esto es la forma de seguir el camino (f_(t),x_(t)), a través de una nueva cota del número de pasos (es el trabajo Bézout VI, publicado en 2009): la longitud en la métrica del condicionamiento. A partir de la nueva cota, surge la necesidad de fijar el algoritmo. Pronto, él mismo y otros autores se interesan en el diseño de buenos métodos de continuación: C. Beltrán, P. Burgisser, F. Cucker, J.-P. Dedieu, A. Leykin y G. Malajovich, con diversas contribuciones que aparecerán a partir del año 2011. Ahora mismo se puede decir que la forma de aproximar el camino (f_(t),x_(t)) una vez que se ha fijado el par inicial (f₍₀₎,x₍₀₎) se entiende completa, o casi completamente.
5. Simultáneamente a la aparición de Bézout VI, Beltrán y Pardo refinarán sus trabajos del 2006 al 2009, obteniendo un nuevo algoritmo más rápido y de más sencilla implementación, publicado en 2011, que se puede considerar el “estado del arte” en lo que se refiere a la elección del par inicial actualmente. Avances posteriores, aunque publicados antes, por Beltrán y Shub (Bezóut VII) analizan otras cantidades como la varianza del tiempo de ejecución del método.

La forma de elegir el par inicial propuesta por Beltrán y Pardo es:

1. Primero se demuestra que si se elige un sistema  f₍₀₎ al azar (con respecto una cierta distribución de probabilidad) y entonces se elige al azar una solución x₍₀₎ de f₍₀₎ (dando a todas la misma posibilidad de ser elegidas), entonces el par (f₍₀₎,x₍₀₎) es, con alta probabilidad, un buen candidato para par inicial del método de homotopía.
2. Para el lector quedará claro que el primer punto no resuelve el problema: escoger un cero  al azar de un sistema de ecuaciones elegido al azar parece una tarea difícil, sobre todo porque se supone que estamos intentando aprender a resolver sistemas de ecuaciones… Uno puede pensar al revés: escojamos primero una solución y luego un sistema (usando que los sistemas que se anulan en un determinado lugar son un subespacio lineal del conjunto total de sistemas). Lamentablemente este proceso no funciona. Sin embargo, hay una alternativa que sí que funciona. El proceso es difícil de explicar en pocas palabras, pero básicamente funciona como sigue: primero se escoge al azar una matriz de n filas y n+1 columnas. Con probabilidad uno, su núcleo tiene dimensión 1. Tomamos un representante de ese núcleo como nuestra solución x₍₀₎, y tomamos f₍₀₎ tal que su “parte lineal” está representada por la matriz que escogimos, añadiendo un término no-lineal elegido al azar.  Se puede demostrar que este proceso, sencillo de implementar en un ordenador, es equivalente a elegir un cero al azar de un sistema de ecuaciones elegido al azar.

Con algunos detalles técnicos más, se completa así el esquema a seguir en los métodos de homotopía, y este método encontrará aproximadamente un cero de un sistema dado, “rápidamente” (esto es, en un tiempo cuadrático en el tamaño input) en media. Este es el algoritmo más eficiente existente hasta la fecha para resolver sistemas de ecuaciones polinomiales. Burgisser y Cucker han propuesto una alternativa que evita la elección al azar a cambio de perder un poco de rapidez en la ejecución del algoritmo. ¡La veda está abierta para tratar de encontrar pares iniciales que garanticen una ejecución del algortimo tan rápida como sea posible!

La práctica, como sucede con muchos métodos numéricos, va muy por delante de la teoría y, si el usuario está dispuesto a admitir un cierto grado (razonable en muchos casos) de incertidumbre en los cálculos entonces puede utilizar alguno de los paquetes de software que implementan el método de homotopía de forma rápida (aunque sin garantía total ni análisis de complejidad). Los paquetes más populares son HOM4PS2, Bertini, PHCpack y NAG4M2 (estos dos últimos se pueden usar con el paquete matemático de software abierto Macaulay2).