![]()
La vida logística
Como comentábamos en nuestra entrada La vida exponencial, el modelo de Thomas Robert Malthus no era muy realista, así que el matemático belga Pierre François Verhulst propuso otro modelo, la ecuación o función logística. Verhults nació en Bruselas el 28 de octubre de 1804 y falleció el 15 de febrero de 1849 en la misma ciudad.

La familia de Pierre Verhulst no escatimó gastos para que pudiera tener una educación de la mayor calidad, y así estudió en uno de los mejores centros de su época, el Ateneo de Bruselas. El joven Verhulst destacó en todos los campos, especialmente en matemáticas, compartiendo honores con Joseph Plateau y Guillaume-Adolphe Nerenburger al graduarse en 1822. Tuvieron un excelente profesor de matemáticas, Adolphe Quetelet, con el que le unió después una gran amistad. En ese año, Verhulst inicia sus estudios de matemáticas en la Universidad de Gante, en la que se reencuentra con Quetelet como profesor de álgebra. Tras unos inicios con algunas dificultades, comienza a destacarse por su capacidad matemática.
Se doctora en 1825 con una tesis sobre las ecuaciones bibnomiales, y es contratado como profesor de análisis matemático en el Museo de Ciencias y Letras de Bruselas en 1827. Pero su mala salud (quizás por la tuberculosis, no se sabe a ciencia cierta) hace que abandone las clases, aunque seguirá estudiando e investigando.

En 1830 se produjo la independencia de Bélgica de los Países Bajos, y Verhulst, que había sido muy activo a pesar de su enfermedad y había sugerido muchas reformas, fue requerido por Quetelet para ayudarle a elaborar tablas de mortalidad en el nuevo estado belga. También Quetelet fue el que lo lleva en 1834 a la recién creada Academia Militar por el rey Leopoldo I, para impartir clases de matemáticas. En 1835 pasa a ser profesor de la Universidad Libre de Bruselas.
Aunque Verhulst hizo importantes contribuciones a las matemáticas, especialmente en el estudio de las funciones elípticas, su gran obra es Notice sur la loi que la population suit dans son accroissement, publicada en 1838. Quetelet había propuesto que el crecimiento exponencial que dictaba la ley de Malthus debería estar corregida con fuerzas que evitaban ese crecimiento, dependiendo del cuadrado de la tasa de crecimiento, pero Verhulst tenía una visión mucho más clara, y decía que “sabemos que el famoso Malthus demostró el principio por el que la población humana crece en progresión geométrica de manera que se dobla cada veinticinco años. El incremento virtual de la población debe estar limitado por el tamaño y la ferlididad del país. De manera que la población se irá acercando cada vez más a una situación estacionaria”.
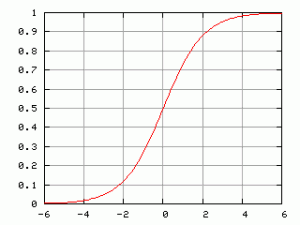
En este y en el posterior artículo de 1844, Recherches mathématiques sur la loi d’accroissement de la population, Verhulst propone como modelo de crecimiento, la ecuación logística (nombre propuesto por él mismo). Se supone que la tasa de reproducción es proporcional a la población existente y también a la cantidad de recursos disponibles. Así que si P representa el tamaño de la población y t el tiempo, se deduce que
dP/dt = r P (1 – P/K)
donde r es la tasa de crecimiento y K la constante de persistencia (relacionada con la capacidad total de población que el sistema pudiera albergar).
Verhulst publicó un tercer trabajo en 1847, Deuxième mémoire sur la loi d’accroissement de la population, en el que criticaba su propio trabajo. Esto motivó que la ecuación cayera en el olvido hasta que fue redescubierta por Raymond Pearl y Lowell Reed en 1920.
A pesar de su fallecimiento prematuro a los 44 años, el año antes a su muerte fue elegido Presidente de la Academia Belga de Ciencias. Siempre será recordado por su ecuanimidad en los debates, y su enorme sentido del deber, que a pesar de sus dificultades físicas le hacía caminar cada día una hora por las calles de Bruselas hasta llegar exhausto a su despacho.
____
Manuel de León (CSIC, Fundador del ICMAT, Real Academia de Ciencias, Real Academia Canaria de Ciencias, ICSU).

Es excelente
[…] Publicado por Matemáticas y sus fronteras el 7 junio, 2018 Comentarios (0) TweetComentábamos en una entrada anterior sobre Pierre Verhuslt que era de saludo delicada, aquejado de una enfermedad crónica sobre la que […]