![]()
Clasificando nudos
Seguimos hablando de nudos en Matemáticas y sus fronteras. Decíamos en la entrada anterior que el interés por los nudos decayó al probarse que las teorías que trataban de explicar con ellos el mundo atómico no se sustentaban a tenor de los nuevos descubrimientos sobre la inexistencia del éter y la aparición de la mecánica cuántica. Pero los matemáticos sí seguían interesados en el tema.
Los topólogos se sintieron fascinados por estos objetos matemáticos. Y una de las cuestiones claves es la de su clasificación, es decir, ¿cuándo podemos decir que dos nudos son equivalentes? Por ejemplo, los dos nudos que exhibimos arriba. Es un tema sutil, porque dos nudos pueden aparecer como muy diferentes pero ser idénticos desde el punto de vista topológico.
Para precisar estas ideas, vayamos a una primera definicíón de equivalencia. Dos nudos N1 y N2 se dirán equivalentes si existe un homeomorfismo
h : R3 —> R3,
que preserva la orientación del espacio y que transforma un nudo en el otro, es decir h(N1) = N2. Digamos que un homeomorfismo es una transformación que que es continua y que tiene inversa y ésta también es continua. La continuidad refleja que preserva en un cierto sentido que se puede precisar matemáticamente la cercanía de los puntos del espacio. Sobre la orientación, decir que hay dos posibles en R3 y h las debe preservar, es decir, no puede convertir una en la opuesta.
Existe otra definición de equivalencia en la que los dos nudos son equivalentes si existe una familia parametrizada de homeomorfismos por un parámetro t entre 0 y 1 que transforma el primer nudo en el segundo (esta familia es lo que se llama una homotopía). Sin embargo, esta definición y la primera son equivalentes. En cualquier caso, resulta complejo y arduo usar directamente estas definiciones.
Diagramas de nudos
Decíamos en una entrada previa que una manera de tratar con los nudos era proyectarlos en un plano y trabajar con esas proyecciones. Una manera de verlo es pensar que ponemos un foco de luz sobre el nodo tridimensional y vemos su sombra en una pared. Habrá intersecciones que se corresponden con los cruces del nodo. Trabajando con algo de cuidado se puede conseguir que estas proyecciones contengan toda la información del nudo. Así, el problema de ver si dos nudos son equivalentes o no se reduce a estudiar si lo son sus proyecciones.
El matemático alemán Kurt Werner Friedrich Reidemeister (1893 –1971) ideó en 1927 un procedimiento (llamado los movimientos de Reidemeister) que nos permite pasar de una proyección regular de un nudo a otra usando solo los siguientes tres tipos de movimientos sobre partes del diagrama en cuestión:
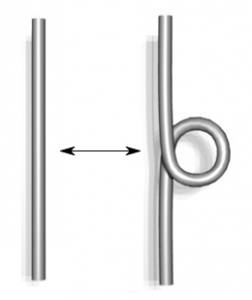
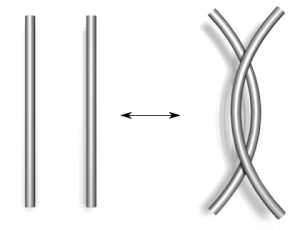
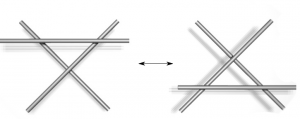
El primer movimiento (tipo I) consiste en girar o crear un lazo; el segundo (tipo II) desplaza un trozo de nudo sin que se cruce con otro trozo; y el tercer movimiento (tipo III) consiste en pasar un trozo de nudo sin cruzamientos sobre o bajo un cruce. El resto del diagrama no se modifica.

Algunos datos sobre Kurt Reidemeister
Reidemester comenzó su carrera matemática en Teoría algebraica de números, bajo la dirección de Erich Hecke, pero tan pronto defendió su tesis su intereés se fue a la geometría diferencial y a la teoría de nudos. En 1923 fue contratado como profesor en la Universidad de Viena (lo que le permitió escapar de la situación empobrecida de la Alemania de postguerra tras el tratado de Versalles y la hiperinflación) , y en 1925 se trasladó a la Universidad de Königsberg. En 1933, su posición pública al régimen nazi le supuso su cese (del que por cierto se enteró leyendo el periódico). Restituido por la presión de sus colegas al gobierno (encabezada por Wilhelm Blaschke) tuvo sin embargo que mantener ocultas sus discrepancias políticas. Tras la guerra y con una estancia en Princeton, fue nombrado profesor en la Universidad de Gotinga hasta su jubilación. Su libro Knoten und Gruppen (1926) es hoy en día un clásico sobre teoría de nudos.
___
Manuel de León (CSIC, Fundador del ICMAT, Real Academia de Ciencias, Real Academia Canaria de Ciencias).




[…] Un nudo se describe matemáticamente como una curva cerrada embebida en el espacio tridimensional y que no tiene autointersecciones. El nudo más simple sería un círculo. Uno de los grandes problemas en la llamada Teoría de Nudos es su representación plana, y como no, la clasificación, en el sentido de que dos nudos son equivalentes si se puede transformar uno en otro sin alterar su topología (las definiciones precisas se pueden encontrar aquí: Clasificando nudos). […]