![]()
Π, donde la geometría se cruza con el análisis
Uno de los números más apreciados por los matemáticos es el número pi (π), hasta el punto de que se ha solicitado que el 3 de marzo sea declarado por la UNESCO como Día Internacional de las Matemáticas. De hecho, hoy ya se celebra esta fecha como el Día de pi en todo el mundo. ¿Qué tiene de especial pi?
Pi es un número conocido desde la antigüedad, definido como la relación entre la longitud de una circunferencia y su diámetro. Y de esta relación viene su nombre, del griego περιφέρεια (periferia) y περίμετρον (perímetro). El primero en usar esta notación fue el matemático y clérigo inglés William Oughtred (1574-1660), inventor también de otros símbolos matemáticos que usamos con frecuencia. Posteriormente, el matemático galés William Jones (1675-1749) propuso usar este símbolo. Y, como siempre, es el gigante Leonhard Euler, el que consigue que todos aceptemos esta notación.

Una pregunta natural es averiguar quién probó que la relación entre el perímetro de un círculo y su diámetro es constante, y he encontrado en esta entrada de Gaussianos, ¿Quién fue el primero que probó que “la constante del círculo” (Pi) es constante?, una respuesta: La cosa está (no podía ser de otra manera) entre Euclides y Arquímedes. Os invito a leer esa entrada, vale mucho la pena.
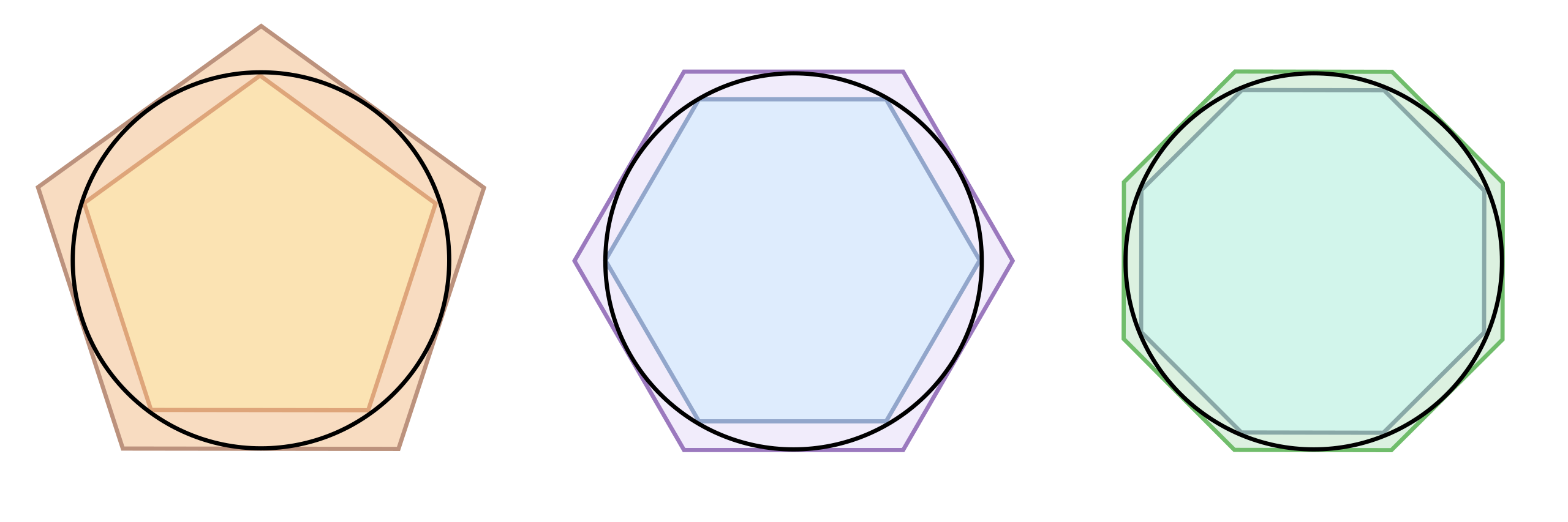
La segunda cuestión para los matemáticos era averiguar el valor de pi. Y sobre esto ya hay mucha literatura escrita: aproximaciones en la Biblia en el Libro de los Reyes, aproximaciones en el famoso papiro de Rhind, y también con los babilonios. Debemos destacar los cálculos de Arquímedes, quién utilizó un método recursivo aproximando el círculo por polígonos regulares inscritos y circunscritos, cada vez con más lados y más pequeños. Calculaba los perímetros de los polígonos e iba aproximando cada vez más el valor de pi. Este método lo usaron más tarde los matemáticos indios Aryabhata y Brahmagupta.
Podíamos decir que pi estaba ligado solo a la geometría, estando presente en cualquier fórmula de áreas o volúmenes que se precie, pero es precisamente cuando se comienza a interpretar pi en relación con la suma de series cuando se está en condiciones de conseguir aproximaciones cada vez más precisas. Durante décadas, este fue un desafío en el que participaron muchos matemáticos.
Pi es un número irracional, es decir, no se puede escribir como una fracción con dos enteros. Esto lo probó el matemático suizo Johann Heinrich Lambert en 1761. Más tarde, en 1882, el matemático alemán Ferdinand von Lindemann provó que es además trascendental, es decir, no se puede obtener como raíz de una ecuación algebraica. Hoy en día, el cálculo de los decimales de pi se hace con ordenadores (por ejemplo, John von Neumann usó el ordenador ENIAC para ello).
Existe una relación curiosa entre el número pi y los números primos, que viene de la solución de Euler al llamado problema de Basilea. Pero también pi está relacionado con la Teoría de Probabilidades, tal y como demostró Buffon con su problema de la aguja.
En fin, pi es un número que ha crecido también en la cultura popular, dando lugar a libros, películas y hasta canciones. Hoy, Día de Pi, Matemáticas y sus fronteras no podía dejar de conmemorarlo.
____
Manuel de León (CSIC, Fundador del ICMAT, Real Academia de Ciencias, Real Academia Canaria de Ciencias).


[…] Matemáticas y sus fronteras -… […]
[…] Uno de los números más apreciados por los matemáticos es el número pi (π), hasta el punto de que se ha solicitado que el 3 de marzo sea declarado por la UNESCO como Día Internacional de las Matemáticas. De hecho, hoy ya se celebra esta fecha como el Día de pi en todo el mundo. ¿Qué tiene de especial pi? Pi es un número conocido desde la antigüedad, definido como la relación entre la longitud de una circunferencia y su diámetro. Y de esta relación viene su nombre, del griego περιφέρεια (periferia) y περίμετρον (perímetro). El primero en usar esta notación fue el matemático y clérigo inglés William Oughtred (1574-1660), inventor también de otros símbolos matemáticos que usamos con frecuencia. Posteriormente, el matemático galés William Jones (1675-1749) propuso usar este símbolo. Y, como siempre, es el gigante Leonhard Euler, el que consigue que todos aceptemos esta notación. Leonhard Euler Una pregunta natural es averiguar quién probó que la relación entre el perímetro de un […]
La información que compartió con nosotros fue muy útil.
Afortunadamente, he leído este artículo y tengo más información sobre pi
He intentado calcular la longitud de
La circunferencia prescindiendo de
Pi. El resultado es que ésta es la hipotenusa
De un triángulo rectángulo cuyos catetos
Son tres veces el diámetro en uno de ellos
Y una vez en el otro. No sé si esto es correcto
I’ll have to follow you because the information you offer is accurate and objective, and it’s pretty beneficial for society’s development.