![]()
Sopa de letras: Más allá del modelo SIR
En entradas anteriores hemos hablado del modelo SIR y de su exitosa trayectoria desde sus orígenes. Por eso, no es de extrañar que un siglo después siga siendo el modelo de referencia en Epidemiología Matemática. No obstante, siguiendo la máxima pragmática, un modelo es tan bueno como su capacidad para ser útil. En este sentido, algunas objeciones al modelo SIR han impulsado el desarrollo de variantes que describiremos en este artículo y aproximaciones alternativas, como las variantes estocásticas o los modelos en “red” (epidemic networks) que reservamos para futuras entradas en este blog.
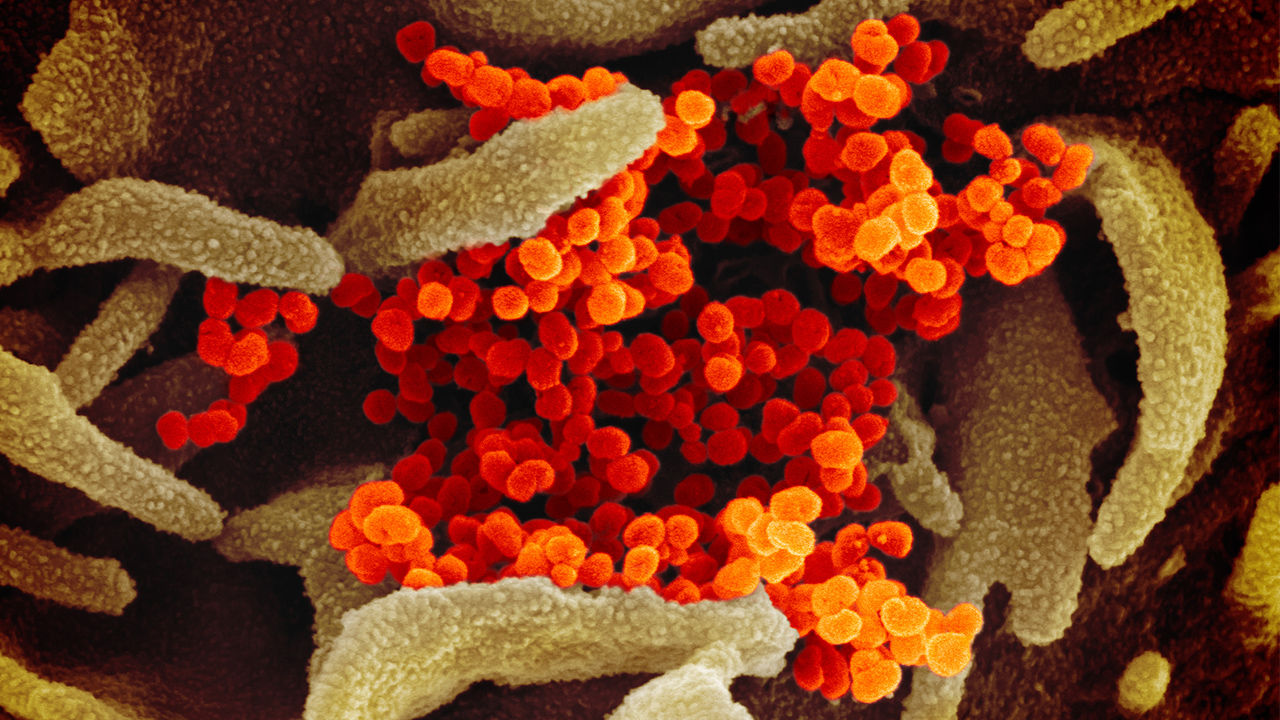
Imagen por microscopio electrónico del SARS-CoV-2 (en naranja). Fuente: National Institute of Allergy and Infectious Diseases
La Biología no actúa de manera instantánea: el modelo SEIR
La primera objeción más frecuente es que el término de la derecha de la ecuación para la evolución de los susceptibles
implica indirectamente que un infectado se vuelve infeccioso instantáneamente. Evidentemente, el virus infecta progresivamente al sujeto, aunque los síntomas sólo se aprecian unos días después de la infección. Como discutimos en El aspecto del enemigo, uno de los desafíos del SARS-CoV-2 es el tiempo en el que un infectado es asintomático, pero puede infectar a otros susceptibles. El modelo SEIR incluye un estado intermedio, E (abreviatura de “Expuestos”), que trata de simular ese periodo de latencia. No siempre los individuos etiquetados en el estado E transmiten la enfermedad; por ejemplo, en el caso de la tuberculosis, se refiere a un estado anterior a la infección activa y durante el cual los bacilos – de la especie Mycobacterium tuberculosis – están en fase latente, de manera que el individuo está infectado pero no puede transmitir la tuberculosis a otros, pero porta bacilos latentes en su organismo que, tarde o temprano, progresarán hacia una infección activa.

Este modelo introduce mucha flexibilidad al incorporar dos nuevos parámetros, el tiempo de latencia, tL, y la probabilidad de que un sujeto asintomático sea infeccioso, e. Es el más utilizado estos días para hacer predicciones cuantitativas de la epidemia de coronavirus, algunas destacadas en prensa, como aquellas de los grupos de Imperial College, Oxford, o las iniciativas colectivas CEMAT o Healthdata.
Si recuerdan de nuestras entradas anteriores, definimos el ritmo (o factor) reproductivo básico, R0, como el número medio de contagios propagados por cada persona contagiada. Para el modelo SIR este parámetro tomaba el valor
Bajo la luz del modelo SEIR, este parámetro toma la forma
Es decir, el modelo SIR subestima R0. Eso son malas noticias, aunque tiene bastante sentido: los sujetos asintomáticos siguen propagando la infección, aunque no sean conscientes de ello, con probabilidad e, y su impacto aumenta con el tiempo medio de latencia, tL.
¿Es el confinamiento o la vacunación la solución a nuestros problemas?
La siguiente pregunta que podemos hacernos concierne la eficacia (a nivel epidemiológico, no a nivel biológico) de vacunar a la población. Esto se puede hacer antes del brote de la epidemia, en cuyo caso, nuestro modelo sería idéntico a un modelo SIR o SEIR, salvo por el hecho de que la población susceptible sería sólo una fracción de la población total; es decir, es necesario incorporar un nuevo estado V para aquellos individuos sobre los que la vacuna induce algún grado de protección. Otra interpretación de este tipo de intervención es el confinamiento que estamos sufriendo estos días. En este escenario, los pacientes diagnosticados son hospitalizados y aislados para evitar que contagien a otros susceptibles. En tal caso, el modelo suele denominarse SITR (Figura 2).
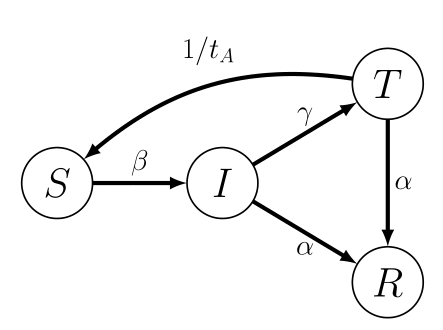
El estado T también puede entenderse como un modelo con cuarentena (Q, del inglés quarantine) en el que los pacientes infectados diagnosticados son aislados. Este modelo también es muy versátil porque se pueden contemplar situaciones en las que después del aislamiento y durante un tiempo tA, una fracción δ sigue siendo infecciosa. En este caso, R0 tomaría el valor
donde γ es inversamente proporcional al tiempo medio que se tarda en detectar a un nuevo infectado y ponerle en aislamiento. De nuevo, el modelo arroja mucha información sobre la importancia de realizar tests a la población (a través del parámetro γ) y de ser cautelosos con las altas hospitalarias hasta garantizar que los pacientes no son infecciosos (a través de tA).
Durante la epidemia del SARS-CoV-1 (el predecesor del Covid-19), algunos grupos utilizaron un modelo generalizado de éste (¡que casi contiene todas las letras del alfabeto!) llamado SEQIJR (Figura 3), que permite distinguir entre estar en cuarentena (Q) y estar aislado (J).

No obstante, como dice el saber popular, a veces menos es más y los modelos complejos (con muchas letras en su nombre) traen consigo una significativa incertidumbre en sus parámetros que puede limitar su utilidad predictiva, por lo que no siempre son “mejores” desde un punto de vista práctico.
¿Qué pasa si no se desarrolla inmunidad perfecta?
Nuestra última sopa de letras trata de responder a una pregunta que está en el aire estos días: ¿qué pasará si después de haber estado infectado, se puede recaer de nuevo?
Para responder a esta pregunta, se ha estudiado una familia de modelos conocidos genéricamente como modelos “endémicos”, todos ellos variantes del modelo SIRS.
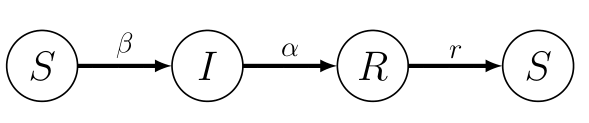
En este caso, existe un equilibrio “endémico” en el que siempre habrá una fracción de la población infectada que puede dar lugar a ciclos de epidemia que se perpetúan periódicamente. La gripe estacional es un ejemplo de enfermedad endémica que, gracias a la vacunación masiva de sujetos susceptibles de alto riesgo, se mantiene bajo cierto control. Desgraciadamente, la gripe se cobra una factura de miles de fallecidos en España todos los años – y cerca del medio millón en todo el mundo –, por lo que no debemos minimizar el impacto de esta enfermedad tan común y generalizada.
Todos estos modelos comparten un aspecto común: todos predicen un crecimiento exponencial y un aplanamiento de la curva. No obstante, no dejan de ser modelos simplificados y pequeños cambios en la estimación de los parámetros, o una mala calidad de los datos hace muy complicado predecir el resultado final de la epidemia. No obstante, esperamos haber convencido al lector de la utilidad y versatilidad de las matemáticas para entender las epidemias y los mecanismos de intervención más eficaces. También confiamos en que, cuando las circunstancias lo permitan, el lector pueda impresionar a amigos y parientes con esta fascinante sopa de letras que les hemos traído hoy.
—
Mario Castro Ponce (Universidad Pontificia Comillas), Manuel de León (Instituto de Ciencias Matemáticas CSIC, Real Academia de Ciencias) y Antonio Gómez Corral (Universidad Complutense de Madrid)

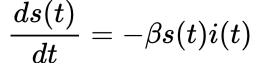
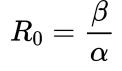

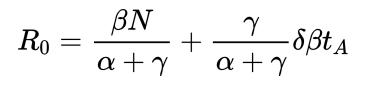
Muy buena explicación, me ha aclarado mucho.
Yo lo aplico desde redes de flujo que es lo que estoy explicando ahora a mis alumnos y funciona muy bien, mejor con más nodos para facilitar la toma de decisiones. Con la aplicación al COVID he conseguido que los alumnos muestren más interés. Se pueden simular distintos escenarios y ver cómo cambia la situación y determinar claramente las funciones objetivo, cuellos de botella, etc.
Un saludo a todos!
[…] básico R0 de los modelos epidémicos, como puede observar el lector comparando esta entrada con otras entradas recientes sobre las matemáticas del coronavirus, y las matemáticas contra la malaria y el modelo SIR. Esa […]
[…] definen, como en las variantes del modelo SIR, cuatro posibles estados para un individuo de la población en cuestión: S (susceptible), I […]
[…] a su control son muy variadas. Hemos comentado en este blog sobre modelos como el modelo SIR y sus variantes, o aquellos donde se usan cadenas de Markov. En ellos se mezclan herramientas determinísticas, […]
Gracias bro, me salvaste de morir de hambre
Great information. Thank you for the wonderful information. I hope more information will come. By the way, please visit our website to find out more about affordability
[…] a su control son muy variadas. Hemos comentado en este blog sobre modelos como el modelo SIR y sus variantes, o aquellos donde se usan cadenas de Markov. En ellos se mezclan herramientas determinísticas, […]
simular distintos escenarios y ver cómo cambia la situación y determinar claramente las funciones objetivo, cuellos de botella, etc.
Un saludo a todos!
By the way, please visit our website to find out more about affordability
narios y ver cómo cambia la situación y determinar claramente las
Thanks for this sharing your tour study. You can enjoy your day by playing would you rather games with your friends
[…] Con todo, la realidad es que la dinámica de la epidemia no sigue tan solo un crecimiento exponencial incontrolado. Por eso los epidemiólogos utilizan modelos matemáticos, para capturar todas las sutilezas de su propagación. Los modelos más habituales dividen la población en grupos (llamados «compartimentos») que describen los conjuntos de individuos susceptibles, asintomáticos, enfermos, hospitalizados u otros. Distintos modelos incluyen más o menos detalles y dan lugar a una auténtica sopa de letras. […]