![]()
El saltamontes caótico
“El aleteo de una mariposa en Brasil puede provocar un tornado en Texas” es la frase mítica que define la Teoría del Caos. Pero, ¿fue siempre así o lo de la mariposa implica que en este caos la poesía triunfó sobre las matemáticas y la física?
Esta frase surge de la presentación de Edward Lorenz durante la 139ª reunión de la Asociación Americana para el Avance de la Ciencia, en diciembre de 1972. Lorenz redescubrió el caos de una manera casual. Como él mismo cuenta:
“En un momento dado, decidí repetir algunos de los cálculos para examinar lo que estaba ocurriendo con más detalle. Paré el ordenador, tecleé una línea de números que había salido de la impresora un poco antes y volví a ponerlo en marcha. Fui a tomar un café y volví una hora más tarde, durante la cual el ordenador había simulado unos dos meses de tiempo. Los números que salían de la impresora no tenían nada que ver con los anteriores.”
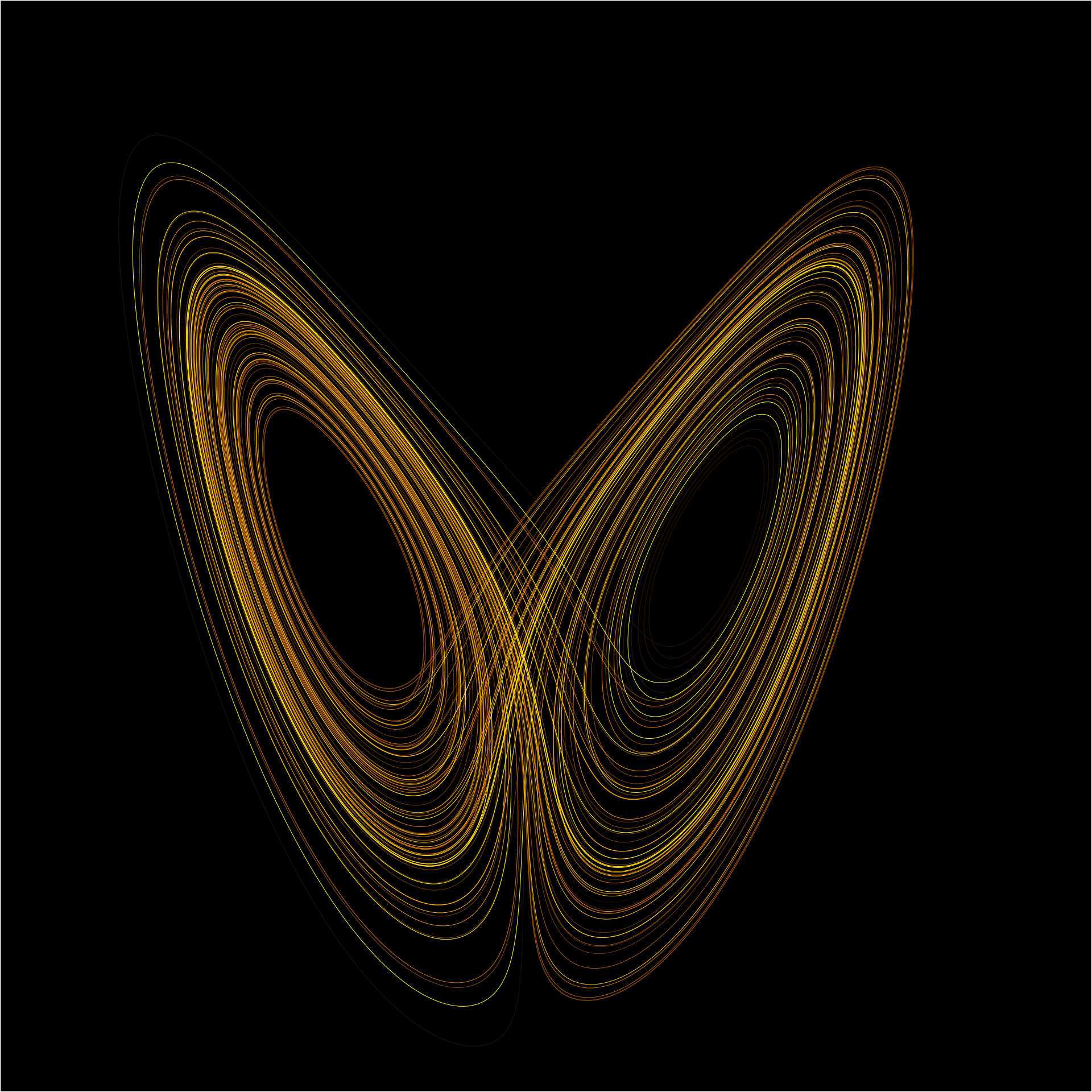
Lo que había ocurrido es que no había considerado todos los decimales tal y como había hecho antes. En su sistema (el ahora llamado atractor de Lorenz), un pequeño cambio en las condiciones iniciales puede producir cambios enormes a largo plazo. Es la “sensibilidad a las condiciones iniciales” que resume la esencia del caos.
Y decimos que redescubrió el caos (término acuñado por el profesor James Yorke, de la Universidad de Maryland), porque ya lo había hecho Henri Poincaré. En 1885, el rey Oscar II de Suecia decidió celebrar su cumpleaños ofreciendo un premio matemático. El tema fue si las matemáticas y las leyes del movimiento serían capaces de probar la estabilidad del Sistema Solar. Poincaré escribió su artículo que resultó ganador, pero cuando Gösta Mittag-Leffler lo imprimió en su prestigiosa revista Acta Mathematica, Poincaré le escribió comunicándole que había cometido un terrible error: había supuesto que si variaba muy poco las condiciones iniciales en sus ecuaciones, esto seguiría así a lo largo del tiempo. Parece que la rectificación le salío bastante más cara que el premio.
Pero volvamos a los lepidópteros. La idea primera para comunicar este efecto caótico fue hablar del aleteo de una gaviota (esto fue idea de un colega de Lorenz). Pero la gaviota no tenía el peso poético de una mariposa.
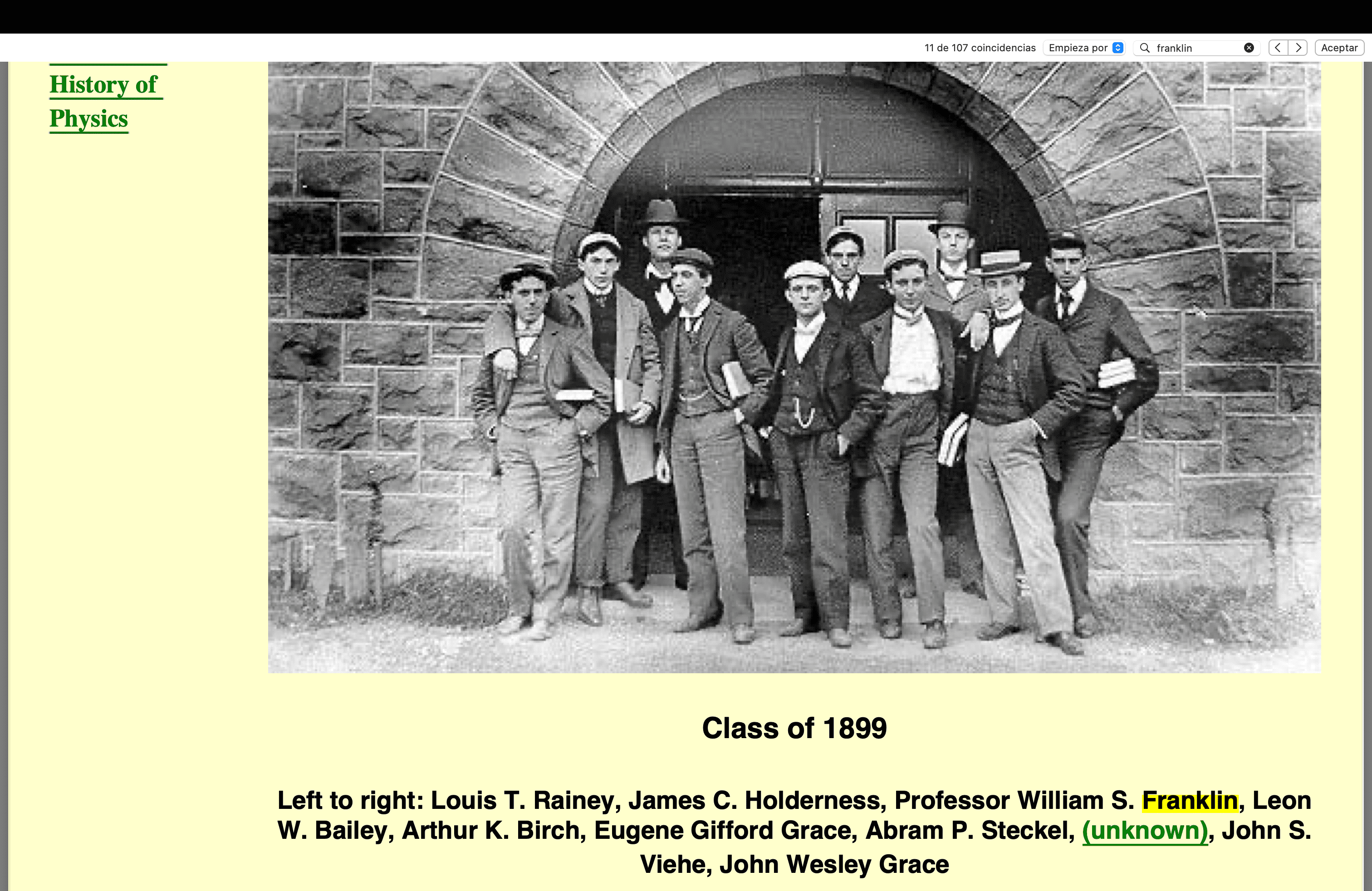
Releyendo el libro de Marcus de Sautoy, Lo que no podemos saber (Acantilado, 2016), descubrí, en el pasaje en el que habla del caos, la referencia a un físico, William Suddards Franklin (1863-1930). En su reseña publicada en 1898 al “Traite Elementaire de Mechanique fondee sur la Thermodynamique·”, de 1987, escrito por Pierre Duhem, se dice:
»La predicción meteorológica detallada a largo plazo es, por tanto, imposible, y la única predicción detallada que es posible es la inferencia de la tendencia final y el carácter de una tormenta a partir de las observaciones de sus primeras etapas; y la exactitud de esta predicción está sujeta a la condición de que el vuelo de un saltamontes en Montana pueda desviar una tormenta desde Filadelfia a Nueva York».
- S. Franklin, Review of P. Duhem, Traite Elementaire de Mechanique fondee sur la Thermodynamique, Paris, 1897″, Vols. 1 and 2, in Phys. Rev. 6, 170–175,1898.
Así que vamos a darle la prioridad a W.S. Franklin y a sus saltamontes, aunque perdamos algo de poesía.

Order Orthoptera — Family Acrididae
Bas-Saint-Laurent — Province de Québec — Canada
Prise en août 2007 — Taken in August 2007
______________
Manuel de León (CSIC, Fundador del ICMAT, Real Academia de Ciencias, Real Academia Canaria de Ciencias, Real Academia Galega de Ciencias).

top drywall company in amarillo thinks this is a fascinating journey through chaos theory! The butterfly effect, as coined by Lorenz, indeed highlights the profound sensitivity to initial conditions.
This is an incredibly interesting exploration of chaos theory! Yes, the extremely sensitive nature to starting points is emphasized by the butterfly effect, a term first proposed by Lorenz. basketball stars
Amazing, sounds intriguing! This topic reminds me of the unpredictable nature of chaos, much like the sporadic leaps of a grasshopper. Speaking of navigating through unpredictability, it’s essential to have reliable support—just like the steady expertise offered by http://www.centralalbertaexcavating.com. Their proficiency in managing the unexpected chaos within excavation projects reflects the precision needed to navigate through uncertain terrains. It’s fascinating how even chaos can be tamed with the right expertise and guidance.
In this chaotic dance between mathematics and poetry, Lorenz’s journey reminds us of the unpredictability that underlies the beauty of chaos theory.
This is a fascinating glimpse into chaos theory for http://www.bridgeportdrywallpros.com!
you are good
This is very timely! Visit us
It’s fascinating how chaos theory emerged from seemingly casual observations.