![]()
La vida exponencial
«The perpetual tendency of the race of man to increase beyond the means of subsistence is one of the general laws of animated nature, which we can have no reason to expect to change.»
Thomas Robert Malthus: Essay on the Principle of Population.
Uno de los números irracionales más interesantes es el número e. Este número, que no aparece hasta que se desarrolla con más profundidad el cálculo, aparece por primera vez en 1618, en las tablas del inventor de los logaritmos, John Napier. Esta es una diferencia con el número pi, de origen geométrico, y conocido desde mucho antes. Aunque el número e no aparecía explcitamente en esta y otras tablas subs tablas de logaritmos de ícitamente en esta y otras tablas posteriores, es Jacob Bernouilli quién en 1683 lo utiliza en su estudio del interés compuesto y determina que su valor debe estar entre 2 y 3.

Leonhard Euler es quién comienza a utilizar de manera sistemática la letra e para representar este número, y en su obra Introductio in Analysin infinitorum, de 1748, hace ya un cálculo aproximado decimal de e, y prueba que es irracional. Será más adelante, en 1873, cuando Charles Hermite demuestre que además es trascendente, es decir, no es una solución de una ecuación algebraica.
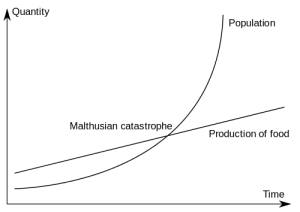
El número e tiene una relevancia esencial en la obra del economista inglés Thomas Robert Malthus, quién en su obra Ensayo sobre el principio de población (An Essay on the Principle of Population, 1798) desarrolla su teoría sobre el crecimiento exponencial de la población frente al crecimiento aritmético de los recursos alimenticios, con lo que en un momento determiando, se produciría la llamada catástrofe malthusiana.
El crecimiento de una población está dado por
P(t) = P0 ert
donde P0 es la población inicial, r es la tasa de crecimiento (llamada parámetro de Malthus), y t es el tiempo. Esta es lo que se llama el primer principio en dinámica de poblaciones.
Digamos algo más sobre la vida de Malthus. Nació en Surrey, el 13 de febrero de 1766 y falleció en Bath, el 29 de diciembre de 1834. Su educación bajo los principios propugnados por el filósofo suizo Jean-Jacques Rousseau en su libro Emilio, influyó notablemente en su vida posterior. Tras estudiar en su propia casa, fue admitido en el Jesus College de Cambridge, donde se graduó en filosofía y teología en 1788, adquiriendo también conocimientos avanzados de matemáticas.Obtiene su máster en 1791 y es elegido fellow (miembro) del Jesus College en 1793. Fue ordenado pastor anglicano en 1797, y en 1804 debe abandonar el college al contraer matrimonio con Harriet Eckersall (de acuerdo con las reglas de la institución). En 1805 es contratado como profesor de historia y economía política en el colegio de la East India Company, en Haileybury, Hertfordshire, escuela cuya función era formar a los funcionarios que después servirían a Inglaterra en destinos de ultramar. Excepto por un viaje a Irlanda y otro al continente europeo, Malthus vivió y trabajó en Haileybury el resto de su vida.
Malthus fue un reconocido miembro de la intelectualidad inglesa, siendo elegido miembro de la Royal Society en 1819, donde contactó con economistas de la talla de David Ricardo y James Mills. Posteriormente fue elegido académico de la Academia Francesas de Ciencias Morales y Políticas y de la Academia de Berlín. Para los estadísticos, será interesante saber que malthus fue uno de los cofundadores de la Sociedad de Estadística de Londres (Statistical Society of London), en 1834.
Malthus publicó su obra cumbre de manera anónima en su primera edición, y en ediciones posteriores fue incorporando nuevo material. El impacto social del pesimismo maltusiano fue enorme, ya que mostraba como políticas sociales basadas en la caridad no resolverían el problema de la miseria.
Se ha criticado posteriormente el trabajo de Malthus, ya que no tuvo en cuenta el control de natalidad, el impacto de las epidemias o la revolución agrícola, pero como suele ocurrir al tratarse de una propuesta empírica, su fortaleza se debilita con el tiempo, al contrario de propuestas con una sólida base teórica.

La teoría de Malthus se aplica en el mundo biológico de una manera directa. Pensemos en como modelizar el crecimiento de bacterias en un cultivo rico en nutrientes. Las bacterias pueden crecer y reproducirse sin ningún problema, y según Malthus, lo harían de una manera exponencial. Es un modelo simple, ya que en algún momento de este crecimiento incontrolado, la población de bacterias desaparecería al acabarse en algún momento los nutrientes.
En entradas posteriores hablaremos de cómo la ley de Malthus fue adaptándose posteriormente para conseguir mejores modelos para la dinámica de poblaciones.
____
Manuel de León (CSIC, Fundador del ICMAT, Real Academia de Ciencias, Real Academia Canaria de Ciencias, ICSU).


[…] y sus fronteras el 28 mayo, 2018 Comentarios (0) TweetComo comentábamos en nuestra entrada La vida exponencial, el modelo de Thomas Robert Malthus no era muy realista, así que el matemático belga Pierre […]
Pretty! This has been an incredibly wonderful post.
Thanks for providing these details. http://www.betfortuna1.com/188bet
Me gusta mucho el artículo sobre el principio en la dinámica de la población que mencionaste anteriormente
This was among the best posts from your team it let me learn many new things.