![]()
Geometría Tropical
Recientemente ha finalizado el semestre en Geometría Tropical de Imdea Matemáticas. Con un título tan exótico no pude evitar ponerme en contacto con uno de los investigadores de esta Fundación y pedirle que me proporcionara una entrada para el blog que explicara en qué consiste este tipo de geometría.

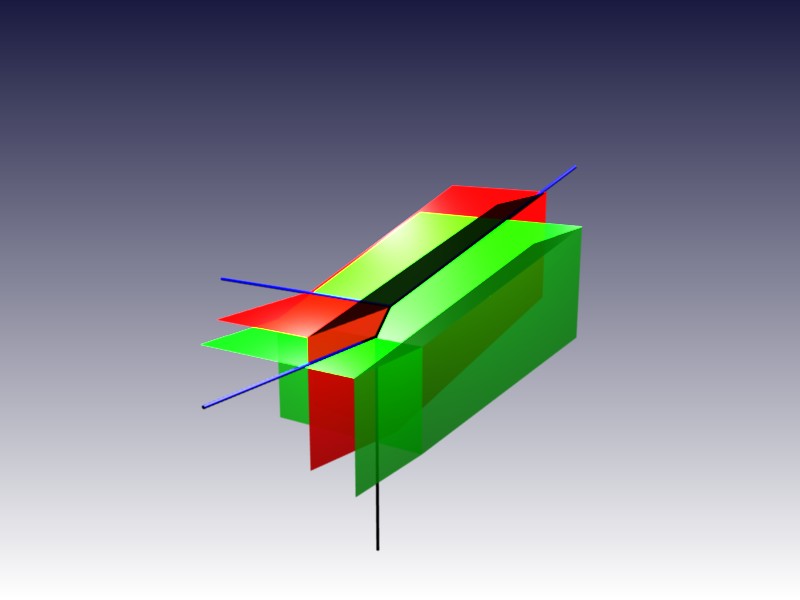
«Dos planos tropicales y su recta intersección»
Seis meses de geometría tropical en IMDEA Matemáticas
La geometría tropical es una rama bastante reciente, los primeros artículos en los que aparece así no tienen más de diez años. Aunque, como siempre, se pueden encontrar trazas de esta disciplina en resultados ya conocidos de antiguo.
Su novedad relativa y lo llamativo del nombre hace que la gente se haga, inevitablemente, dos preguntas: ¿Eso qué es? Seguida de ¿Por qué se le llama tropical?
Sobre tan excéntrico nombre, Speyer y Sturmfels, comentan en un artículo «Tropical mathematics» que este nombre es un homenaje, de algunos matemáticos franceses, al matemático brasileño Imre Simon por sus aportaciones al álgebra min-plus.
Respecto a lo que es, se podría decir que es la geometría creada a partir del álgebra min-plus. Pero esto no aclara nada. Digamos que es una geometría en la que la característica más relevante es que sustituye los objetos geométricos clásicos (rectas, cónicas, superficies) por ciertos complejos poliedrales. Estos complejos poliedrales pueden verse como «una sombra» de los objetos clásicos. Lo curioso es que algunas propiedades geométricas se preservan al hacer esta sustitución, por lo que algunos problemas, que pueden ser complicados de resolver en geometría clásica, se vuelven más sencillos en geometría tropical. O al menos permiten ser tratados con técnicas de la combinatoria, ampliando las herramientas con las que cuenta el matemático a la hora de enfrentarse a los problemas.

«Dos cúbicas tropicales en el plano»
Ya se han cumplido seis meses de la serie de seminarios en geometría tropical que se están impartiendo en la Fundación IMDEA Matemáticas. Diversos especialistas, nacionales e internacionales, han acudido para mostrar resultados y puntos de vista. Aquí presentamos un resumen de lo que se contó en las mismas.
En enero, la serie de seminarios arrancan con las exposiciones de Ilia Itenberg (U. Estrasburgo) y L. F. Tabera (IMDEA Matemáticas). El profesor Itenberg impartió dos seminarios titulados «Tropical Curves» y «Recursive formulas for Welschinger invariants». En estos seminarios se explicaron los conceptos básicos relativos a las curvas tropicales planas: cómo se definen o cómo determinar su grado y género. También explicó la aplicación de la geometría tropical a problemas de geometría enumerativa real y compleja. Mostrando un cálculo tropical de los invariantes de Welschinger y Gromov-Witten en algunos contextos. Por su parte L. F. Tabera contó en su charla «Geometric Constructions in Tropical Geometry» cómo comparar construcciones geométricas en el plano complejo y tropical.
En febrero contamos con las conferenciantes Alicia Dickenstein (U. Buenos Aires) y María Jesús de la Puente (U. Complutense de Madrid). La profesora Dickenstein, en su conferencia «Tropical discriminants» contó como, dada una familia de polinomios, se le puede asociar un polinomio discriminante que captura los casos en los que las soluciones del sistema de polinomios es patológico. Mostró como la tropicalización de este discriminante puede ser calculada sin necesidad de calcular previamente el discriminante algebraico. Por otro lado, la profesora de la Puente dio una visión global de la geometría tropical. Al ser una disciplina tan reciente, aún están bajo estudio y discusión los conceptos más elementales y, por el momento, no hay una única definición de curva tropical o de grado de una curva. En esta charla aprendimos los distintos puntos de vista, cómo se relacionan o las alternativas que hay.
La siguiente conferenciante fue Sonia Rueda (U. Politécnica de Madrid), «Polhyedral representations of invariant differential operators», y que nos habló en abril sobre una aplicación de la combinatoria a problemas fuera de ella. Mostrando los polígonos que se esconden tras los anillos de operadores diferenciales invariantes bajo ciertas acciones en el espacio afín.
Erwan Brugallé (U. Paris 6), con su charla «Floor decomposition of tropical curves» mostró como extender las técnicas tropical planas de conteo de curvas de género y grado fijado que pasan por una familia de curvas al caso en el que las curvas son espaciales. Por su parte, el profesor Francisco Santos (U. Cantabria) habló sobre las distintas posibilidades combinatorias de colocar rectas tropicales en el plano y la relación de estas posibilidades con las triangulaciones del producto de dos simplices en su seminario «Triangulations of products of simplices and tropical geometry».
Finalmente, en Junio, tuvimos la visita de M. Kerber (T.U. Kaiserslautern) con el seminario «A Riemann-Roch theorem in tropical geometry», en el que generaliza una versión combinatoria del teorema de Riemann-Roch sobre grafos a un teorema de Riemman-Roch válido para curvas tropicales. Así como una posible interpretación geométrica del mismo.
La geometría tropical es una rama bastante reciente, los primeros artículos en los que aparece así no tienen más de diez años. Aunque, como siempre, se pueden encontrar trazas de esta disciplina en resultados ya conocidos de antiguo.
Su novedad relativa y lo llamativo del nombre hace que la gente se haga, inevitablemente, dos preguntas: ¿Eso qué es? Seguida de ¿Por qué se le llama tropical?
Sobre tan excéntrico nombre, Speyer y Sturmfels, comentan en un artículo «Tropical mathematics» que este nombre es un homenaje, de algunos matemáticos franceses, al matemático brasileño Imre Simon por sus aportaciones al álgebra min-plus.
Respecto a lo que es, se podría decir que es la geometría creada a partir del álgebra min-plus. Pero esto no aclara nada. Digamos que es una geometría en la que la característica más relevante es que sustituye los objetos geométricos clásicos (rectas, cónicas, superficies) por ciertos complejos poliedrales. Estos complejos poliedrales pueden verse como «una sombra» de los objetos clásicos. Lo curioso es que algunas propiedades geométricas se preservan al hacer esta sustitución, por lo que algunos problemas, que pueden ser complicados de resolver en geometría clásica, se vuelven más sencillos en geometría tropical. O al menos permiten ser tratados con técnicas de la combinatoria, ampliando las herramientas con las que cuenta el matemático a la hora de enfrentarse a los problemas.
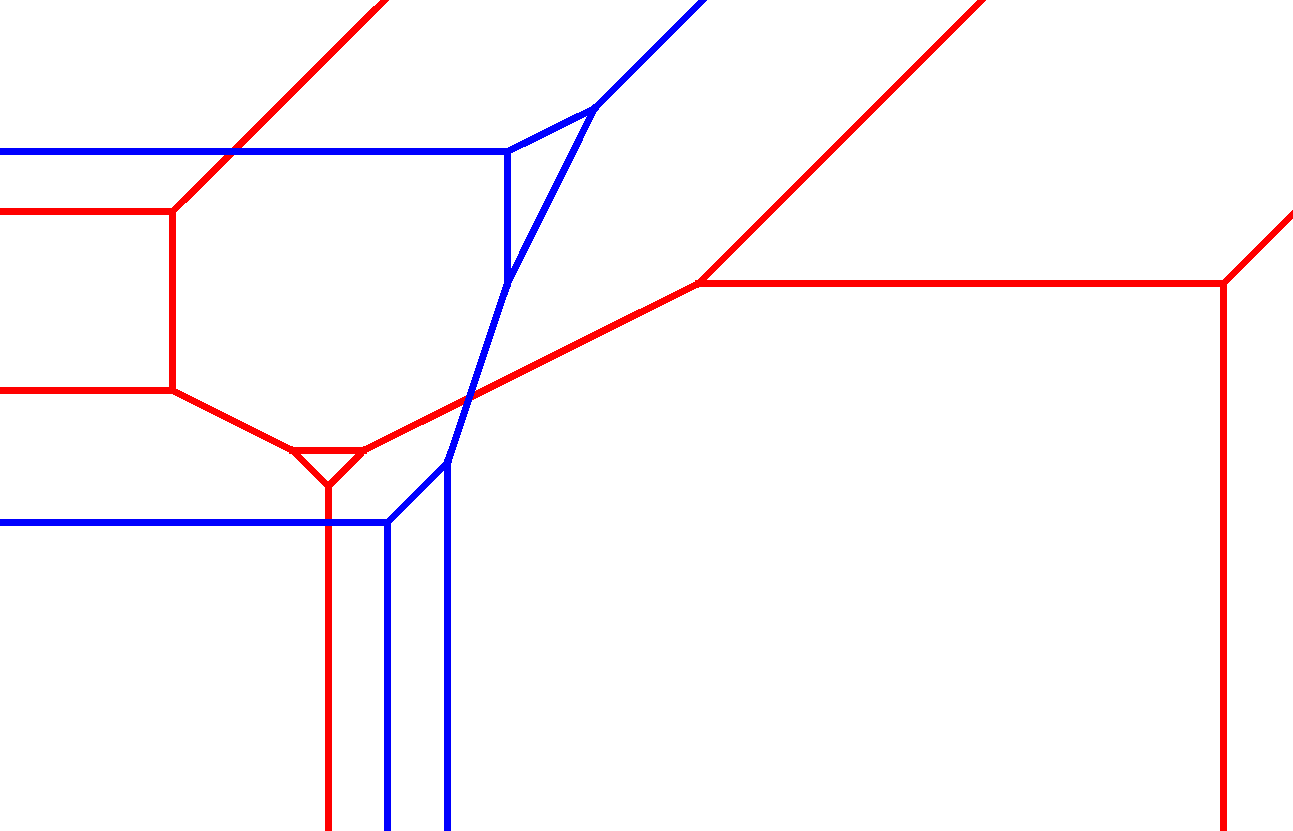
«Dos cúbicas tropicales en el plano»
Ya se han cumplido seis meses de la serie de seminarios en geometría tropical que se están impartiendo en la Fundación IMDEA Matemáticas. Diversos especialistas, nacionales e internacionales, han acudido para mostrar resultados y puntos de vista. Aquí presentamos un resumen de lo que se contó en las mismas.
En enero, la serie de seminarios arrancan con las exposiciones de Ilia Itenberg (U. Estrasburgo) y L. F. Tabera (IMDEA Matemáticas). El profesor Itenberg impartió dos seminarios titulados «Tropical Curves» y «Recursive formulas for Welschinger invariants». En estos seminarios se explicaron los conceptos básicos relativos a las curvas tropicales planas: cómo se definen o cómo determinar su grado y género. También explicó la aplicación de la geometría tropical a problemas de geometría enumerativa real y compleja. Mostrando un cálculo tropical de los invariantes de Welschinger y Gromov-Witten en algunos contextos. Por su parte L. F. Tabera contó en su charla «Geometric Constructions in Tropical Geometry» cómo comparar construcciones geométricas en el plano complejo y tropical.
En febrero contamos con las conferenciantes Alicia Dickenstein (U. Buenos Aires) y María Jesús de la Puente (U. Complutense de Madrid). La profesora Dickenstein, en su conferencia «Tropical discriminants» contó como, dada una familia de polinomios, se le puede asociar un polinomio discriminante que captura los casos en los que las soluciones del sistema de polinomios es patológico. Mostró como la tropicalización de este discriminante puede ser calculada sin necesidad de calcular previamente el discriminante algebraico. Por otro lado, la profesora de la Puente dio una visión global de la geometría tropical. Al ser una disciplina tan reciente, aún están bajo estudio y discusión los conceptos más elementales y, por el momento, no hay una única definición de curva tropical o de grado de una curva. En esta charla aprendimos los distintos puntos de vista, cómo se relacionan o las alternativas que hay.
La siguiente conferenciante fue Sonia Rueda (U. Politécnica de Madrid), «Polhyedral representations of invariant differential operators», y que nos habló en abril sobre una aplicación de la combinatoria a problemas fuera de ella. Mostrando los polígonos que se esconden tras los anillos de operadores diferenciales invariantes bajo ciertas acciones en el espacio afín.
Erwan Brugallé (U. Paris 6), con su charla «Floor decomposition of tropical curves» mostró como extender las técnicas tropical planas de conteo de curvas de género y grado fijado que pasan por una familia de curvas al caso en el que las curvas son espaciales. Por su parte, el profesor Francisco Santos (U. Cantabria) habló sobre las distintas posibilidades combinatorias de colocar rectas tropicales en el plano y la relación de estas posibilidades con las triangulaciones del producto de dos simplices en su seminario «Triangulations of products of simplices and tropical geometry».
Finalmente, en Junio, tuvimos la visita de M. Kerber (T.U. Kaiserslautern) con el seminario «A Riemann-Roch theorem in tropical geometry», en el que generaliza una versión combinatoria del teorema de Riemann-Roch sobre grafos a un teorema de Riemman-Roch válido para curvas tropicales. Así como una posible interpretación geométrica del mismo.
Por Luis Tabera
Investigador de IMDEA Matemáticas
Investigador de IMDEA Matemáticas

Col-Car lleva cuatro meses parado…
encontre interesante el artículo y lo he añadico a noticias argentinas :)…
Es muy interesante, los aportes a esta nueva área
[…] geometría tropical es una reciente y novedosa rama de la geometría algebraica desarrollada desde 1990. El exótico […]